Question

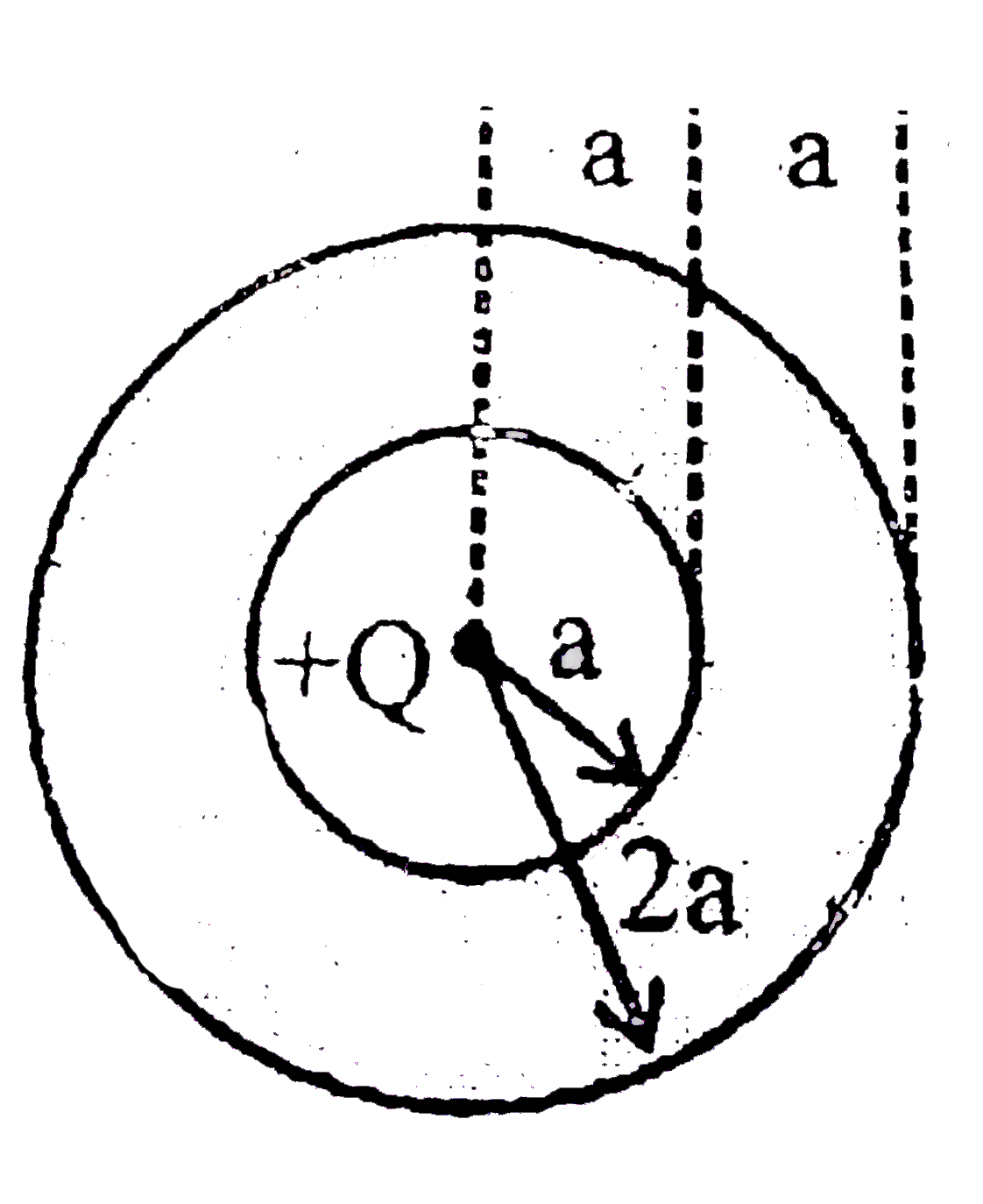
A point charge +Q is placed at the centre of an uncharged spherical conducting shell of inner radius a and outer radius b.
i. Find the electric field for $r<a$.
ii. What is the magnitude and sigh of the induced charge q' on the inner shell surface?
iii. What is the electric field at points $r>b$?
iv. What id the surface charge on the outer surface of the conductor?

Explanation

To solve the problem step by step, we will analyze each part of the question regarding a point charge $$+Q$$ placed at the center of an uncharged spherical conducting shell with inner radius $$a$$ and outer radius $$b$$.

Step 1: Electric Field for \( r < a \)

To find the electric field inside the spherical conducting shell (for \( r < a \)), we can use Gauss's law.

1. Choose a Gaussian surface: A spherical surface of radius \( r \) where \( r < a \).
2. Apply Gauss's law:
\( \Phi_E = \oint \vec{E} \cdot d\vec{A} = \frac{Q_{\text{in}}}{\epsilon_0} \)
Since there is no charge enclosed by the Gaussian surface (the charge \( +Q \) is at the center), we have:
\( Q_{\text{in}} = 0 \)
Therefore, the electric field \( E \) inside the shell is:
\( E \cdot 4\pi r^2 = 0 \implies E = 0 \)

Answer for Part i: The electric field for \( r < a \) is \( E = 0 \).

Step 2: Induced Charge on the Inner Shell Surface

Next, we need to find the magnitude and sign of the induced charge \( q' \) on the inner surface of the shell.

1. Induced charge: The charge \( +Q \) at the center will induce a charge on the inner surface of the conducting shell. By electrostatic induction, the inner surface will have a charge of \( -Q \) to neutralize the field inside the conductor.
2. Total charge on the inner surface:
\( q' = -Q \)

Answer for Part ii: The magnitude and sign of the induced charge \( q' \) on the inner shell surface is \( -Q \).

Step 3: Electric Field for \( r > b \)

Now, we find the electric field outside the spherical conducting shell (for \( r > b \)).

1. Choose a Gaussian surface: A spherical surface of radius \( r \) where \( r > b \).
2. Apply Gauss's law:
\( \Phi_E = \oint \vec{E} \cdot d\vec{A} = \frac{Q_{\text{in}}}{\epsilon_0} \)
The total charge enclosed by this Gaussian surface includes the charge \( +Q \) at the center and the induced charge \( -Q \) on the inner surface. The outer surface must have a charge of \( +Q \) to maintain overall neutrality. Thus, the total enclosed charge is:
\( Q_{\text{in}} = +Q + (-Q) + Q = +Q \)
Therefore, we have:
\( E \cdot 4\pi r^2 = \frac{Q}{\epsilon_0} \implies E = \frac{Q}{4\pi \epsilon_0 r^2} \)

Answer for Part iii: The electric field for \( r > b \) is \( E = \frac{Q}{4\pi \epsilon_0 r^2} \).

Step 4: Surface Charge on the Outer Surface of the Conductor

Finally, we need to find the surface charge on the outer surface of the conductor.

1. Total charge on the outer surface: The outer surface of the conductor must balance the induced charge on the inner surface. Since the inner surface has a charge of \( -Q \), the outer surface must have a charge of \( +Q \) to maintain overall neutrality.

Answer for Part iv: The surface charge on the outer surface of the conductor is \( +Q \).

---