A charge q=10μC is distributed uniformly over the circumference of a ring of radius 3m placed on x-y placed with its centre art origin. Find the electric potential at a point P(0,0,4m)
The correct Answer is:A, D
To find the electric potential at point P(0,0,4m) due to a uniformly charged ring, we can follow these steps:
Step 1: Understand the configuration
The charge q=10μC is uniformly distributed over the circumference of a ring of radius R=3m centered at the origin in the x-y plane. The point P is located at (0, 0, 4m).
Step 2: Calculate the distance from the ring to point P
To find the electric potential at point P, we need to determine the distance r from any point on the ring to point P. The distance can be calculated using the Pythagorean theorem.
The distance from the center of the ring (which is at the origin) to point P is 4 m (along the z-axis). The radius of the ring is 3 m (in the x-y plane).
Using the Pythagorean theorem:
r=√(32)+(42)=√9+16=√25=5m
Step 3: Write the formula for electric potential
The electric potential V at a point due to a point charge is given by:
V=kqr
where k is Coulomb's constant, approximately 8.99×109N⋅m2/C2.
Step 4: Calculate the total electric potential at point P
Since the charge is uniformly distributed over the ring, the potential at point P due to the entire charge can be calculated as:
V=kQr
where Q=10μC=10×10−6C and r=5m.
Substituting the values:
V=(8.99×109N⋅m2/C2)10×10−6C5m
Calculating this gives:
V=(8.99×109)×(2×10−6)=17.98×103V
or
V≈1.798×104V
Final Answer
The electric potential at point P(0,0,4m) is approximately 1.8×104V.
---
The charge q=10μC is uniformly distributed over the circumference of a ring of radius R=3m centered at the origin in the x-y plane. The point P is located at (0, 0, 4m).
To find the electric potential at point P, we need to determine the distance r from any point on the ring to point P. The distance can be calculated using the Pythagorean theorem.
r=√(32)+(42)=√9+16=√25=5m
The electric potential V at a point due to a point charge is given by:
V=kqr
where k is Coulomb's constant, approximately 8.99×109N⋅m2/C2.
Since the charge is uniformly distributed over the ring, the potential at point P due to the entire charge can be calculated as:
V=kQr
where Q=10μC=10×10−6C and r=5m.
V=(8.99×109N⋅m2/C2)10×10−6C5m
V=(8.99×109)×(2×10−6)=17.98×103V
or
V≈1.798×104V
The electric potential at point P(0,0,4m) is approximately 1.8×104V.
Topper's Solved these Questions
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Example Type 5
5 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Example Type 6
4 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions
135 Videos
Similar Questions
A charge of 4×10−9C is distributed uniformly over the circumference of a conducting ring of radius 0.3m. Calculate the field intensity at a point on the axis of the ring at 0.4m from its centre, and also at the centre.
View SolutionA charge q0 is distributed uniformly on a ring of radius R. A sphere of equal radius R constructed with its centre on the circumference of the ring. Find the electric flux through the surface of the sphere.
View SolutionAs charge q=1μC is placed at point (1m,2m,4m). Find the electric field at point P(0,−4m,3m)
View SolutionA charge q=−2.0μC is placed at origin. Find the electric field at (3m,4m,0).
View SolutionA circular ring of radius R and uniform linear charge density +λC/m are kept in x - y plane with its centre at the origin. The electric field at a point (0,0,R√2) is
View SolutionA positive charge Q is uniformly distributed along a circular ring of radius R.a small test charge q is placed at the centre of the ring.

View SolutionA Charge Q is distributed uniformly on a ring of radius r. A sphere of equal r is constructed with its centre at the periphery of the ring (figure 30.12) Find the flux of the electric field through the surface of the sphere.
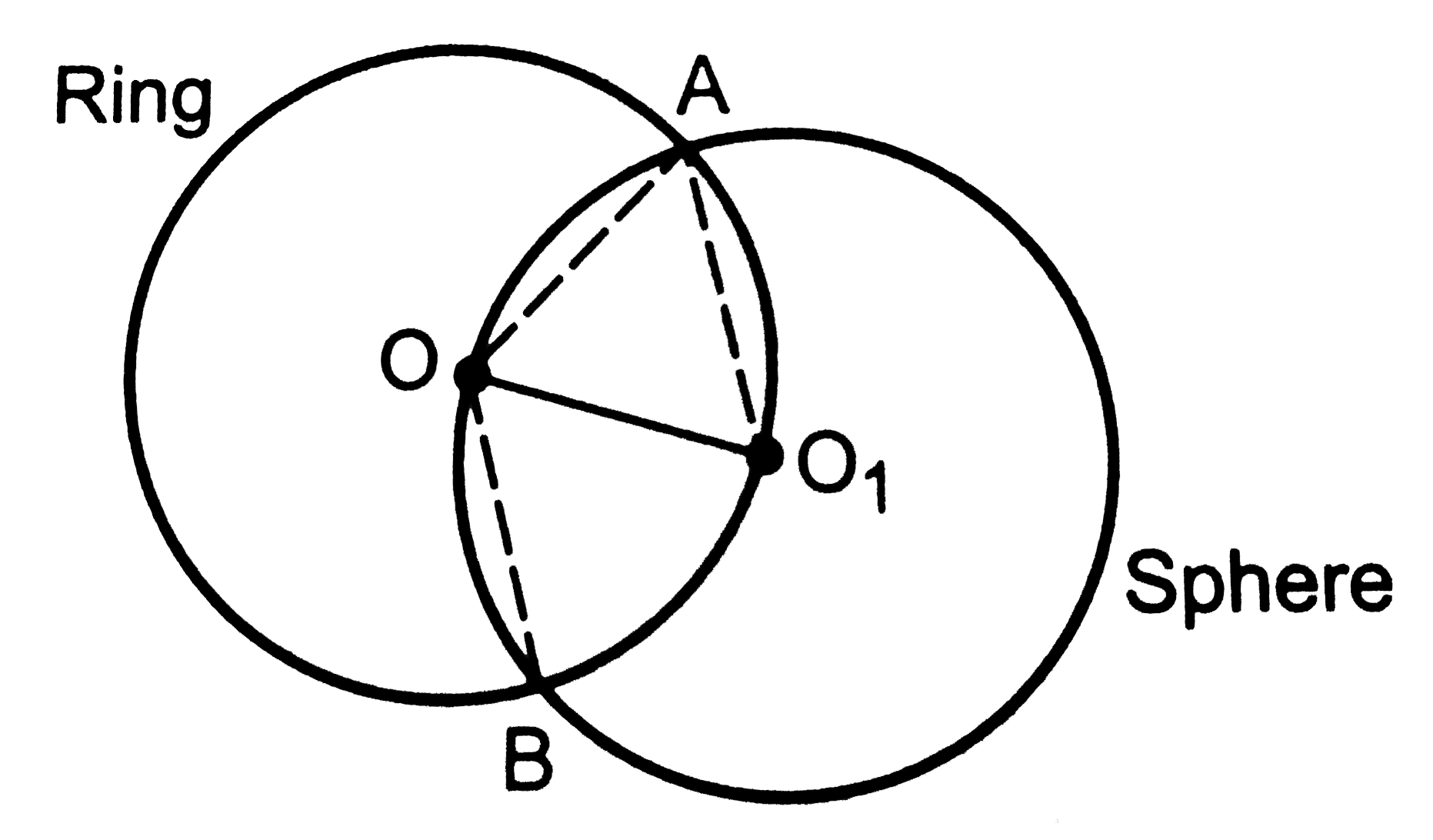
View SolutionA charge q is uniformly distributed over a quarter circular ring of radius r. The magnitude of electric field strength at the centre of the ring will be
View SolutionA positive charge Q is uniformly distributed along a circular ring of radius R.a small test charge q is placed at the centre of the ring .The

View SolutionCharge q is uniformly distributed over a thin half ring of radius R. The electric field at the centre of the ring is
View Solution
