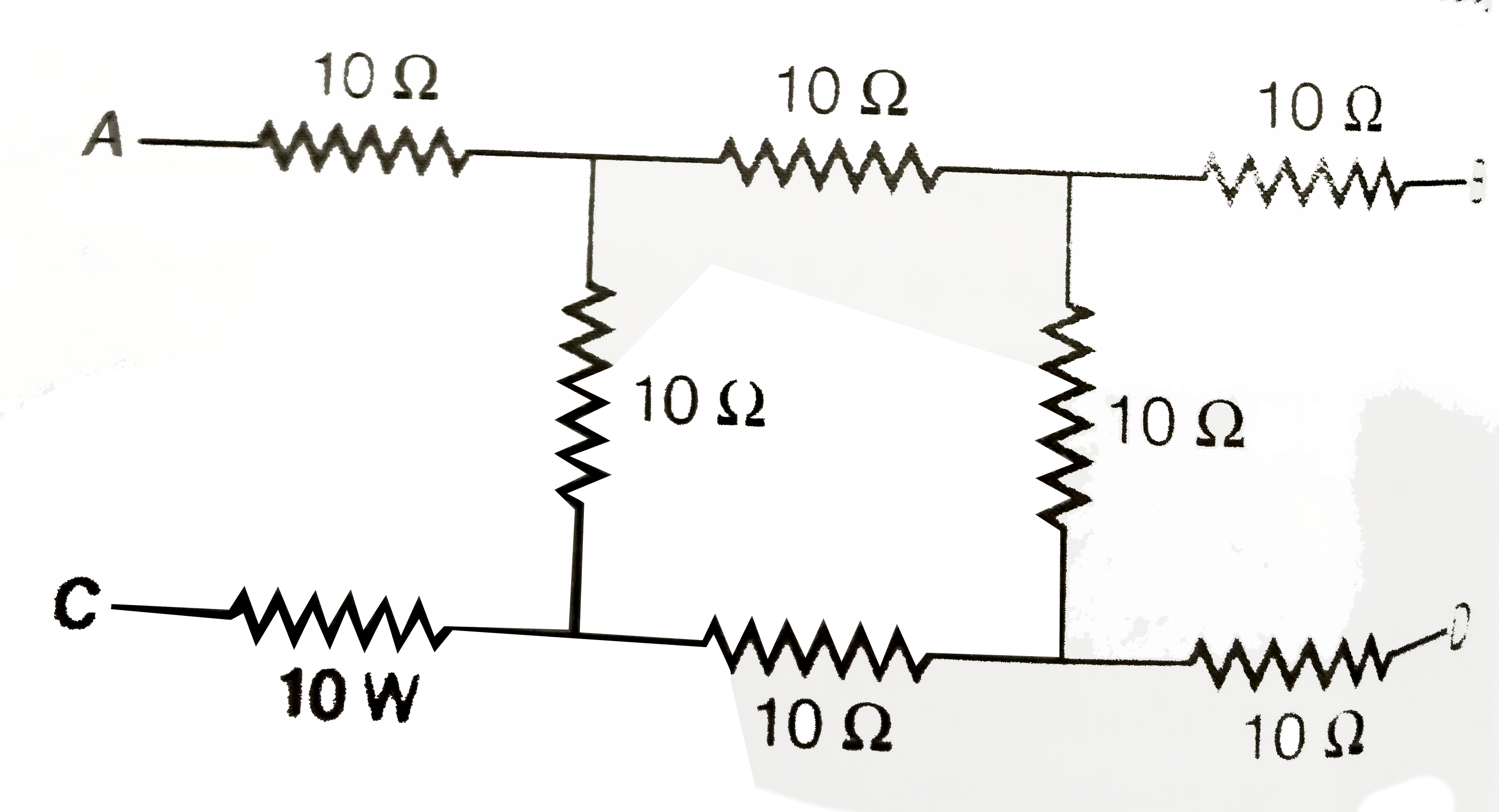
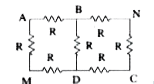
What will be the change in the resistance of a circuit between $A$ and $F$ consisting of five identical conductors, if two similar conductors are added as shown by the dashed line in figure?

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A, B, C

$R_{i} + 5 R$
if connected by two equal resistors betwene $B$ and $D$ and between $C$ and $E$ the combination is a balanced wheatstone bridge and two resistors in series.
$∴ R_{f} = R + R + R = 3 R = 0.6 R_{i}$

Updated on:21/07/2023

|

Class 12 PHYSICS CURRENT ELECTRICITY

Topper's Solved these Questions

Similar Questions

Knowledge Check

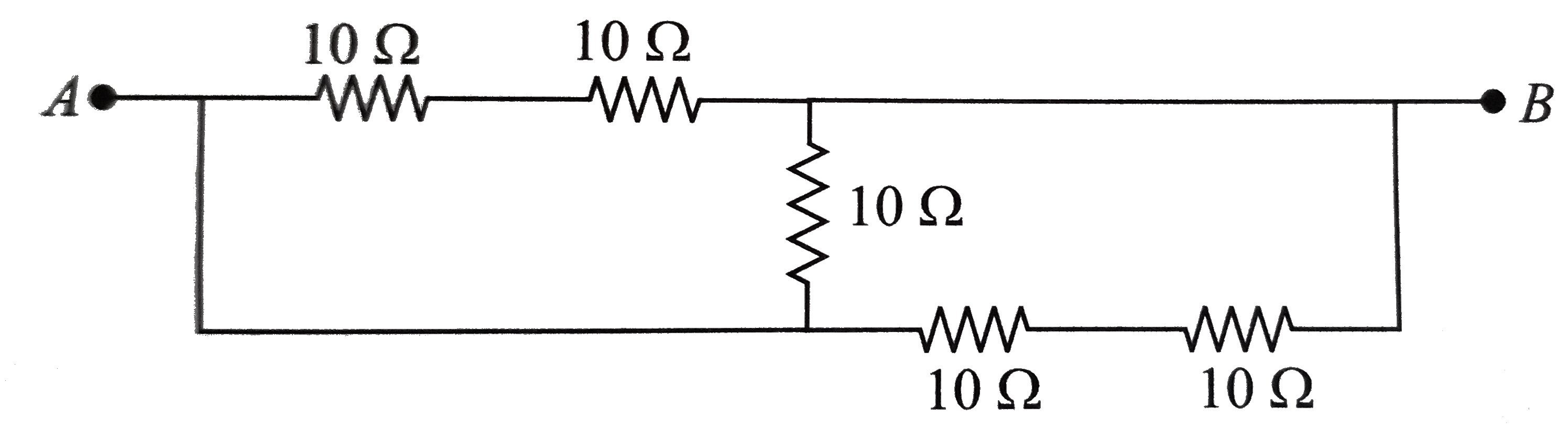
The equivalent resistance between A and B for . the circuit shown in this figure is

A $13.1 Ω$
B $15.1 Ω$
C $17.1 Ω$
D $19.1 Ω$
Five equal resistances of $10 Ω$ are connected between A and B as shown in figure. The resultant resistance

A $10 Ω$
B $5 Ω$
C $15 Ω$
D $6 Ω$

DC PANDEY ENGLISH-CURRENT ELECTRICITY-Level 1 Subjective

Home
Ask Doubt
Profile