A voltmeter of resistance R1 and an ammeter of resistance R2 are connected in series across a battery oif negligible internal resistance. When as resistance R is connected in parallel to voltmeter reading of ammeter increases three times white that of voltmeter reduces to one third. Find the ratio of R1 and R2.
To solve the problem, we need to analyze the situation step by step.
Step 1: Understand the initial setup
We have a voltmeter with resistance R1 and an ammeter with resistance R2 connected in series across a battery with negligible internal resistance. The total voltage across the series combination is equal to the emf of the battery E.
Step 2: Write the equation for the initial condition
In the initial condition, the voltage across the ammeter VA and the voltage across the voltmeter VV can be expressed as:
VA+VV=E
Step 3: Introduce the external resistance
Now, when a resistance R is connected in parallel with the voltmeter, the readings change. The reading of the ammeter increases to three times its initial value, and the reading of the voltmeter reduces to one third of its initial value.
Let the initial reading of the ammeter be I and the initial reading of the voltmeter be VA and VV.
After connecting R in parallel:
- The new reading of the ammeter is 3I
- The new reading of the voltmeter is VV3
Step 4: Write the equations for the new condition
From the new condition, we can write:
3I+VV3=E(Equation 1)
Step 5: Relate the voltages
From the initial condition, we know:
VA=IR2andVV=IR1
Substituting these into Equation 1 gives:
3I+IR13=E
Step 6: Simplify the equation
Multiplying through by 3 to eliminate the fraction:
9I+IR1=3E
This can be rearranged to:
IR1=3E−9I
Step 7: Substitute VA into the equation
From the initial condition, we also have:
VA=IR2⇒I=VAR2
Substituting this into the equation gives:
R1VAR2=3E−9VAR2
Step 8: Rearranging the equation
Multiplying through by R2:
R1VA=3ER2−9VA
Rearranging gives:
R1VA+9VA=3ER2
Factoring out VA:
VA(R1+9)=3ER2
Step 9: Find the ratio of R1 and R2
From the initial condition, we have:
VA=E−VV⇒VV=E−VA
Substituting this into the equation gives:
R1+9=3ER2VA
Using the relationship VV=IR1 and substituting for VA leads to:
R1=3R2
Thus, the ratio of R1 to R2 is:
R1R2=3:1
Final Answer
The ratio of R1 to R2 is 3:1.
---
We have a voltmeter with resistance R1 and an ammeter with resistance R2 connected in series across a battery with negligible internal resistance. The total voltage across the series combination is equal to the emf of the battery E.
In the initial condition, the voltage across the ammeter VA and the voltage across the voltmeter VV can be expressed as:
VA+VV=E
Now, when a resistance R is connected in parallel with the voltmeter, the readings change. The reading of the ammeter increases to three times its initial value, and the reading of the voltmeter reduces to one third of its initial value.
- The new reading of the ammeter is 3I
- The new reading of the voltmeter is VV3
From the new condition, we can write:
3I+VV3=E(Equation 1)
From the initial condition, we know:
VA=IR2andVV=IR1
3I+IR13=E
Multiplying through by 3 to eliminate the fraction:
9I+IR1=3E
This can be rearranged to:
IR1=3E−9I
From the initial condition, we also have:
VA=IR2⇒I=VAR2
Substituting this into the equation gives:
R1VAR2=3E−9VAR2
Multiplying through by R2:
R1VA=3ER2−9VA
Rearranging gives:
R1VA+9VA=3ER2
Factoring out VA:
VA(R1+9)=3ER2
From the initial condition, we have:
VA=E−VV⇒VV=E−VA
Substituting this into the equation gives:
R1+9=3ER2VA
Using the relationship VV=IR1 and substituting for VA leads to:
R1=3R2
R1R2=3:1
The ratio of R1 to R2 is 3:1.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise 23.1
6 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise 23.2
1 Video
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Example Type 6
1 Video
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective
11 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrances gallery
25 Videos
Similar Questions
An ammeter and a voltmeter of resistance R connected in seires to an electric cell of negligible internal resistance. Their readings are A and V respecitvely. If another resistance R is connected in parallel with the voltmeter
View SolutionAn ammeter and a voltmeter of resistance R connected in seires to an electric cell of negligible internal resistance. Their readings are A and V respecitvely. If another resistance R is connected in parallel with the voltmeter
View SolutionAn ammeter, voltmeter and a resistor are connected in series to a cell and the readings are noted as I and V. If another resistor R is connected in parallel with a voltmeter, then
View SolutionIn the circuit shows in Fig. 6.42, resistors X and Y, each with resistance R, are connected to a 6V battery of negligible internal resistance. A voltmeter, also of resistance R, is connected across Y.
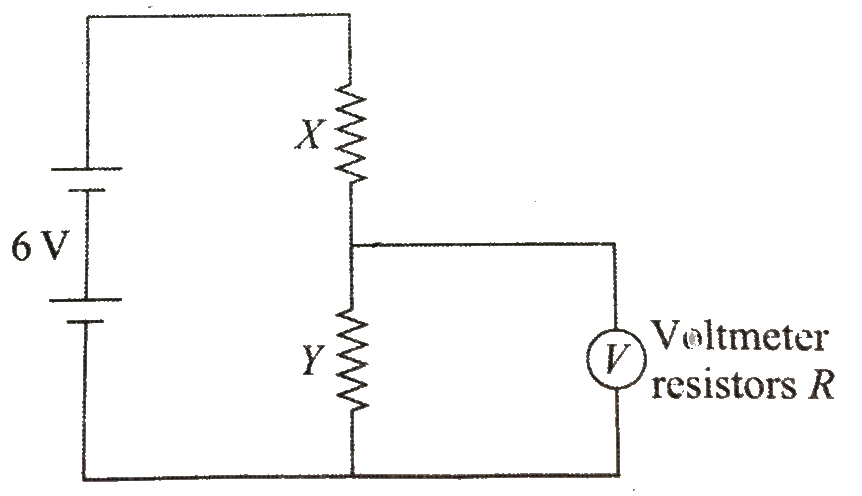
What is the reading of the voltmeter?
View SolutionAn ammeter and a voltmeter are connected in series to a battery with an emf ξ=6.0V. When a certain resistance is connected in parallel with the voltmeter, the readings of the latter decreases η=2.0 times, whereas the readings of the ammeter increase the same number of times, Find the voltmeter readings after the connection of the resistance.
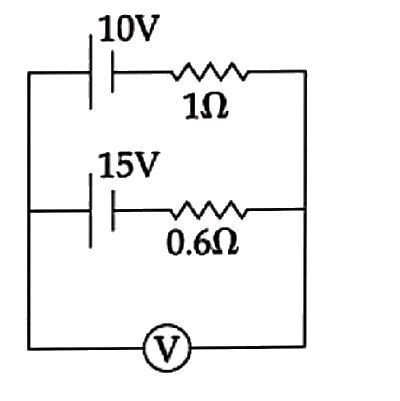
View SolutionA 10 V battery with internal resistance 1Ω and a 15 V battery with internal resistance 0.6Ω are connected in parallel to a voltmeter (see figure). The reading in the voltmeter will be close to:
View SolutionAn ammeter has resistance R0 and range l what resistance should be connected in parallel with it to increase its range by nl ?
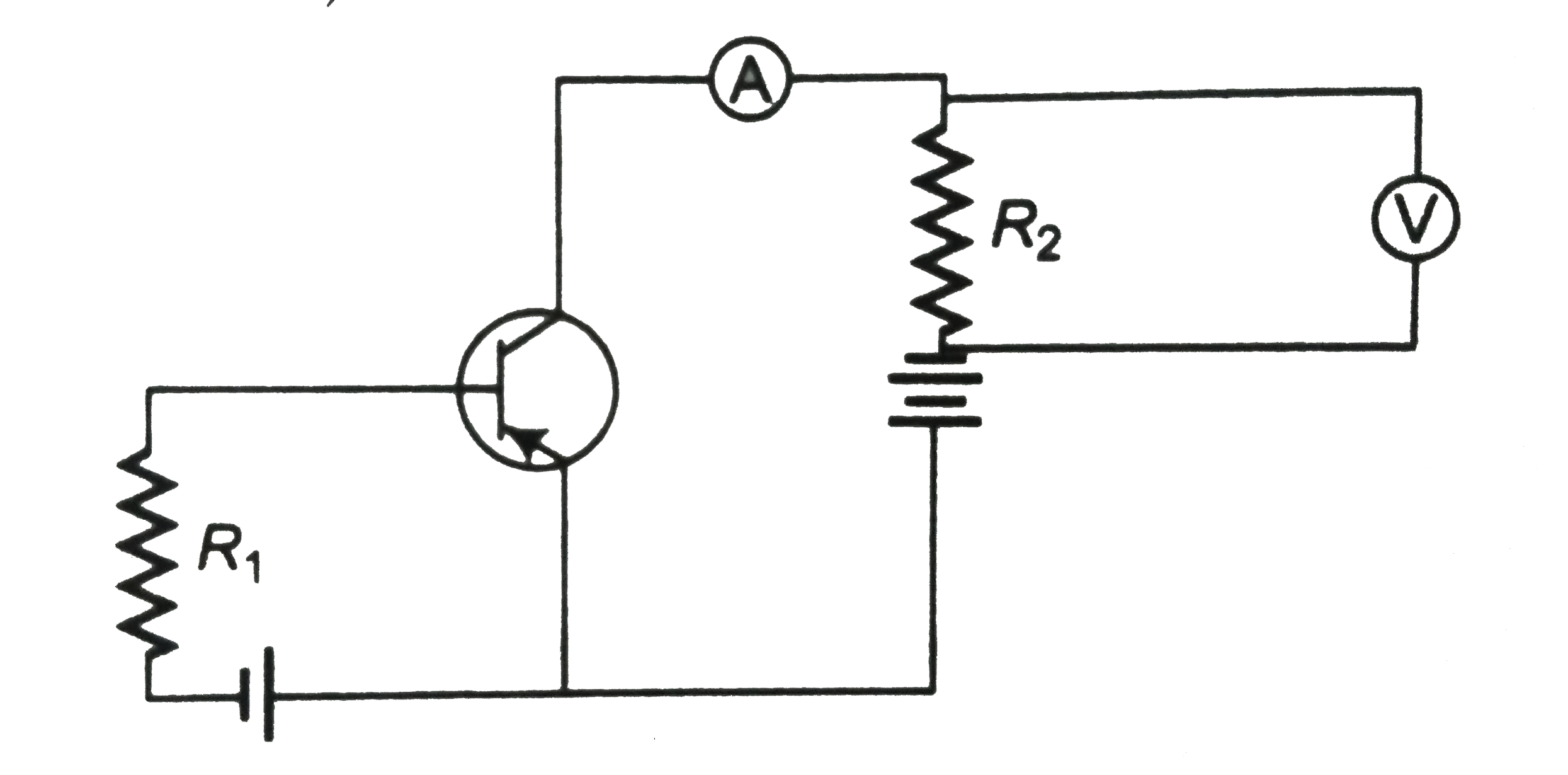
View SolutionIf the resistance R1 is increased , how will the readings of the ammeter and voltmeter change?
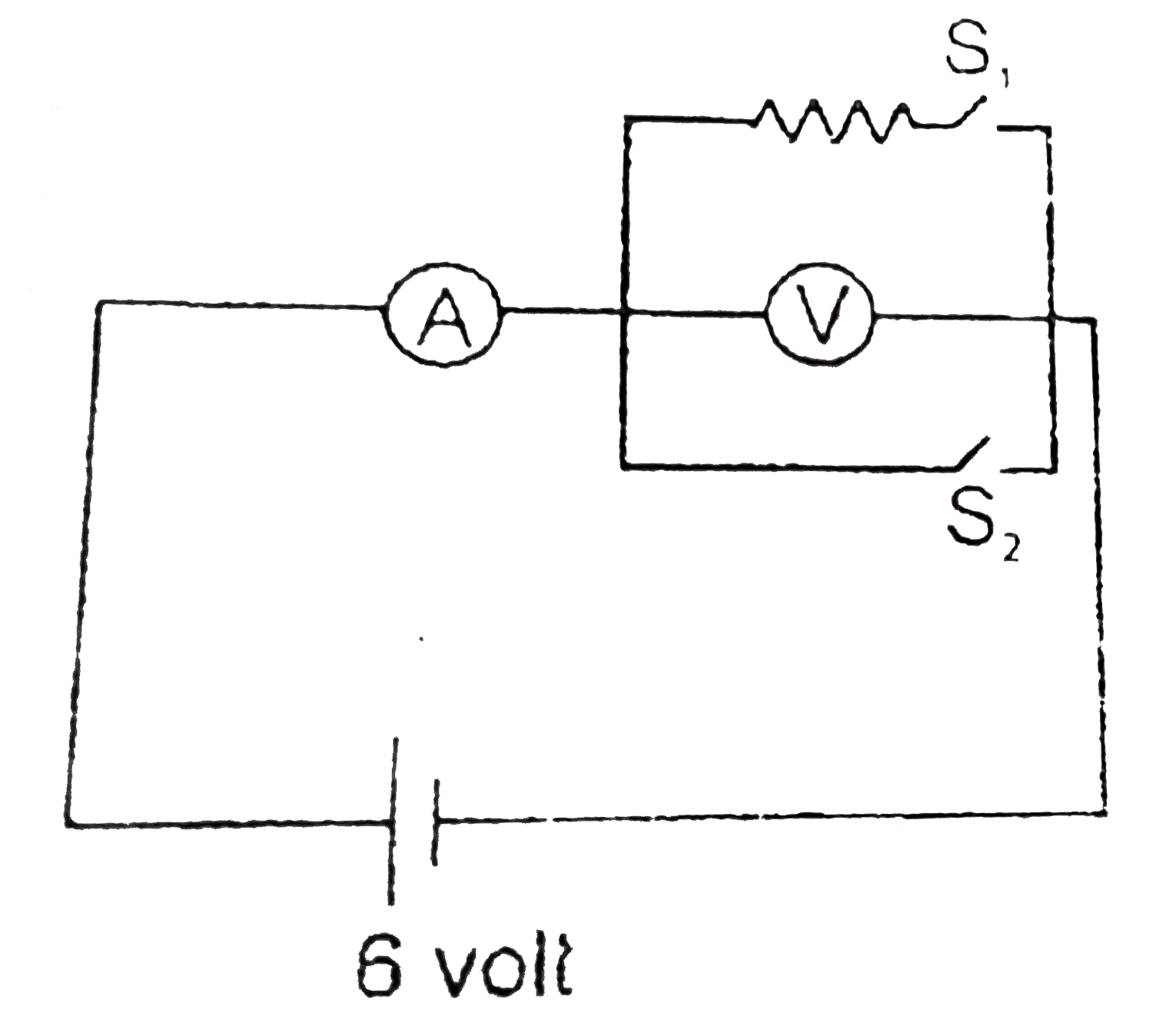
View SolutionAn ammeter and a voltmeter are initially connected in series to a battery of zero internal resistance. When switch S1 is closed the reading of the voltmeter becomes half of the initial, whereas the reading of the ammeter becomes double. If now switch S2 is also closed, then reading of ammeter becomes :
View SolutionAn ammeter and a voltmeter are joined in series to a cell. Their readings are A and V respectively. If a resistance is now joining parallel with the voltmeter. Then
View Solution