A battery has an open circuit potential difference of 6V between its terminals. When a load resistance of 60Ω is connected across the battery,the total power supplied by the bttery is 0.4W. What should be the load resistance R, so that maximum power will be dissipated in R. Calculated this power. What is the total power supplied by the battery when such a load is connected?
To solve the problem step by step, we will follow these steps:
Step 1: Identify the given values
- Open circuit potential difference (emf, E) = 6 V
- Load resistance (RL) = 60 Ω
- Power supplied by the battery (P) = 0.4 W
Step 2: Use the power formula to find the internal resistance
The power supplied by the battery can be expressed using the formula:
P=E2R+r
where R is the load resistance and r is the internal resistance of the battery.
Substituting the known values:
0.4=6260+r
This simplifies to:
0.4=3660+r
Step 3: Solve for internal resistance r
Cross-multiplying gives:
0.4(60+r)=36
Expanding this:
24+0.4r=36
Subtracting 24 from both sides:
0.4r=12
Dividing by 0.4:
r=120.4=30Ω
Step 4: Determine the load resistance for maximum power transfer
For maximum power transfer, the load resistance R should equal the internal resistance r:
R=r=30Ω
Step 5: Calculate the total power supplied by the battery with the new load resistance
Using the power formula again with the new load resistance:
Ptotal=E2R+r
Substituting R=30Ω and r=30Ω:
Ptotal=6230+30=3660=0.6W
Step 6: Calculate the power dissipated in the load resistance
Since both the internal and external resistances are equal, the power dissipated in the load resistance R will be half of the total power supplied:
PR=Ptotal2=0.62=0.3W
Final Answers
- Load resistance R for maximum power transfer: 30Ω
- Total power supplied by the battery when this load is connected: 0.6W
- Power dissipated in the load resistance R: 0.3W
- Open circuit potential difference (emf, E) = 6 V
- Load resistance (RL) = 60 Ω
- Power supplied by the battery (P) = 0.4 W
The power supplied by the battery can be expressed using the formula:
P=E2R+r
where R is the load resistance and r is the internal resistance of the battery.
0.4=6260+r
This simplifies to:
0.4=3660+r
Cross-multiplying gives:
0.4(60+r)=36
Expanding this:
24+0.4r=36
Subtracting 24 from both sides:
0.4r=12
Dividing by 0.4:
r=120.4=30Ω
For maximum power transfer, the load resistance R should equal the internal resistance r:
R=r=30Ω
Using the power formula again with the new load resistance:
Ptotal=E2R+r
Substituting R=30Ω and r=30Ω:
Ptotal=6230+30=3660=0.6W
Since both the internal and external resistances are equal, the power dissipated in the load resistance R will be half of the total power supplied:
PR=Ptotal2=0.62=0.3W
- Load resistance R for maximum power transfer: 30Ω
- Total power supplied by the battery when this load is connected: 0.6W
- Power dissipated in the load resistance R: 0.3W
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise 23.1
6 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise 23.2
1 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Example Type 6
1 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective
11 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrances gallery
25 Videos
Similar Questions
A battery has an open circuit potential difference 10 V between the terminals. When loads 9Ωand4Ω are connected one by one across the battery , the power in the load resistance is the same. The amount of heat approximately generated in one second in the load when a load of 5Ω Is connected across the battery will be
View Solutionthe current in a circuit containing a battery connected to 2Ω resistance is 0.9A. When ana additional resistance of 8Ω is connected to the same battery the current observed in the circuit is 0.3A. Then the internal resistance of the battery is xΩ. Find value of x.
View SolutionEach resistor shown in the figure has a resistance of 10Ω and the battery has the emf 6 V. What will be the current supplied by the battery ?
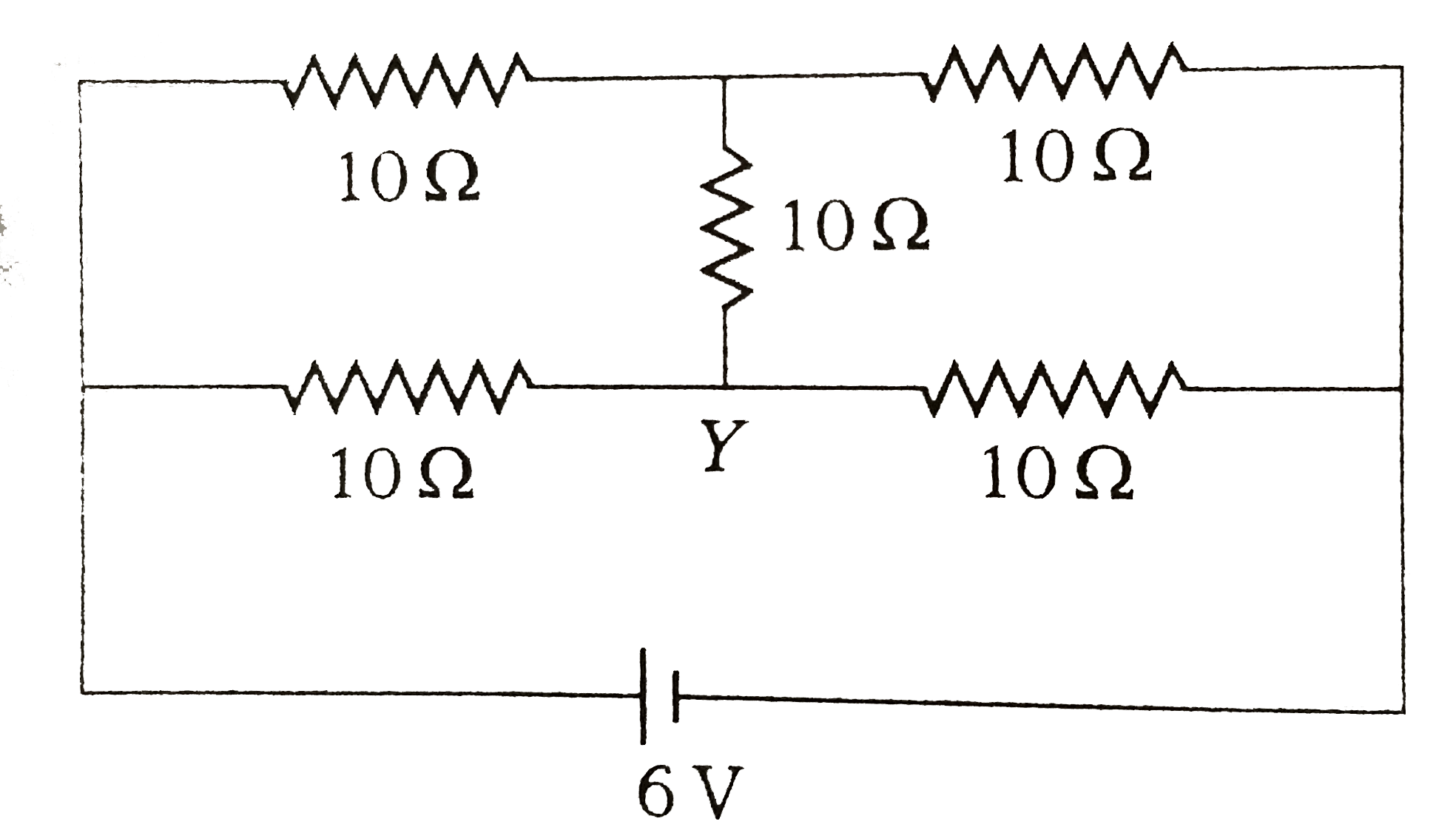
View SolutionIn the circuit shown, total power supplied by an ideal battery is 80 W. if R=10Ω. If the resistance R is removed from the circuit. Then
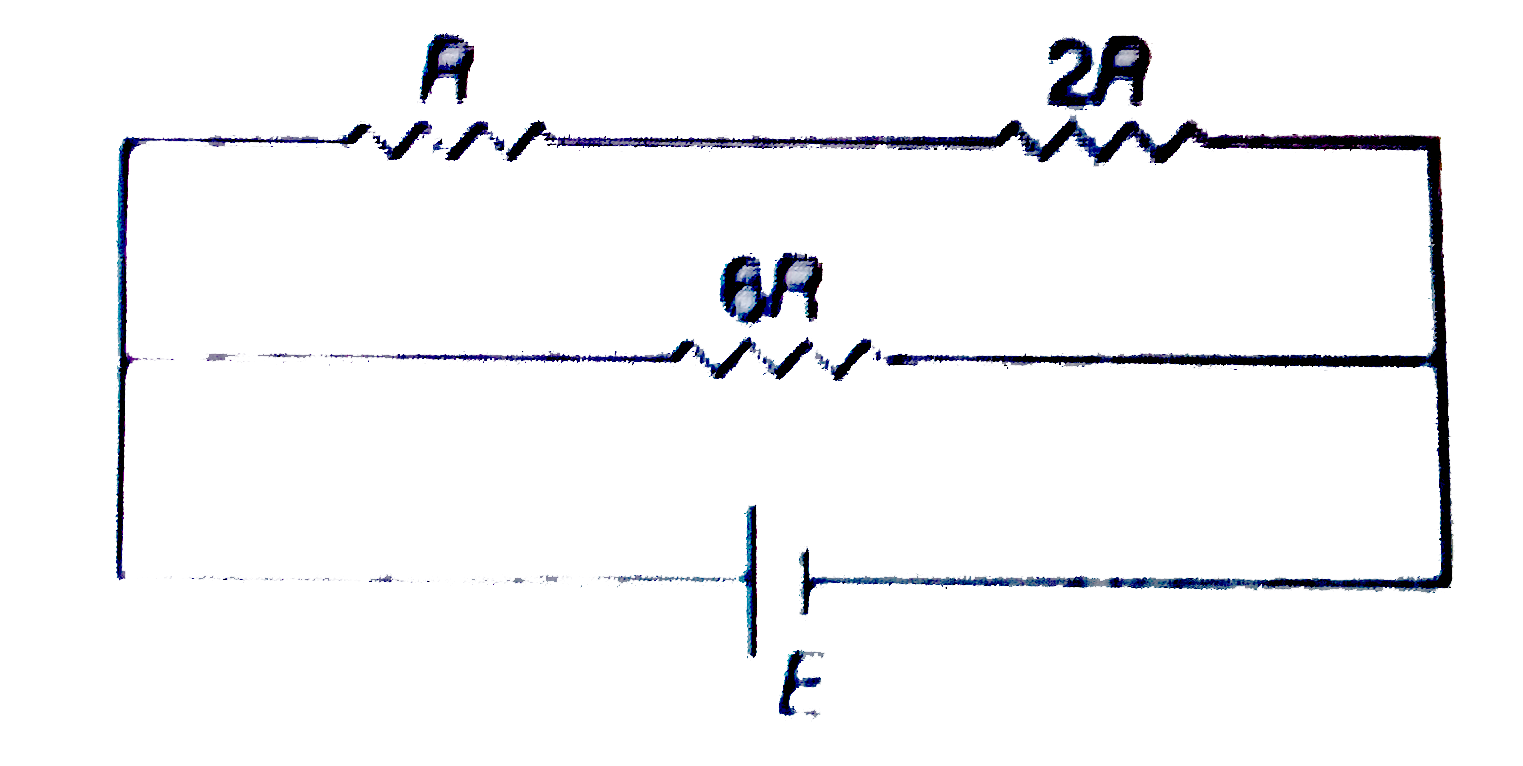
View SolutionThe potential difference between the terminals of a battery of emf 6.0V and internal resistance1(Ω)drops to 5.8 V when connected across an external resistor. Find the resistance of the external resistor.
View SolutionIn the circuit shown, total power supplied by an ideal battery is 80 W. if R=10Ω. Then EMF of the battery is
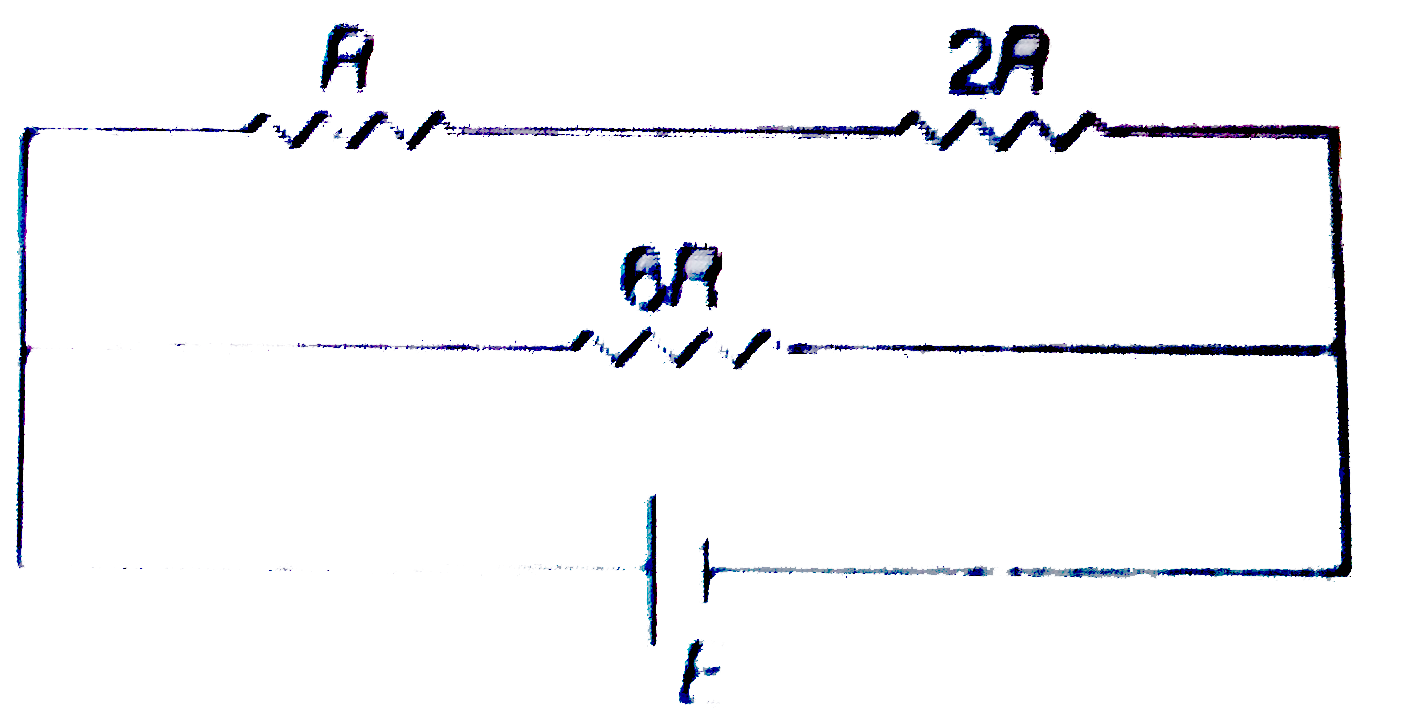
View SolutionA battery of emf 10 V is connected with a load resistance of 50 Omega the total power delivered by the battery is 2 W. If load resistance is replaced by R then power delivered is 4 W, the value of R is
View SolutionIn the circuit shown, total power supplied by an ideal battery is 80 W. if R=10Ω. Then Ratio of power developed across R, 2R and 6R will be
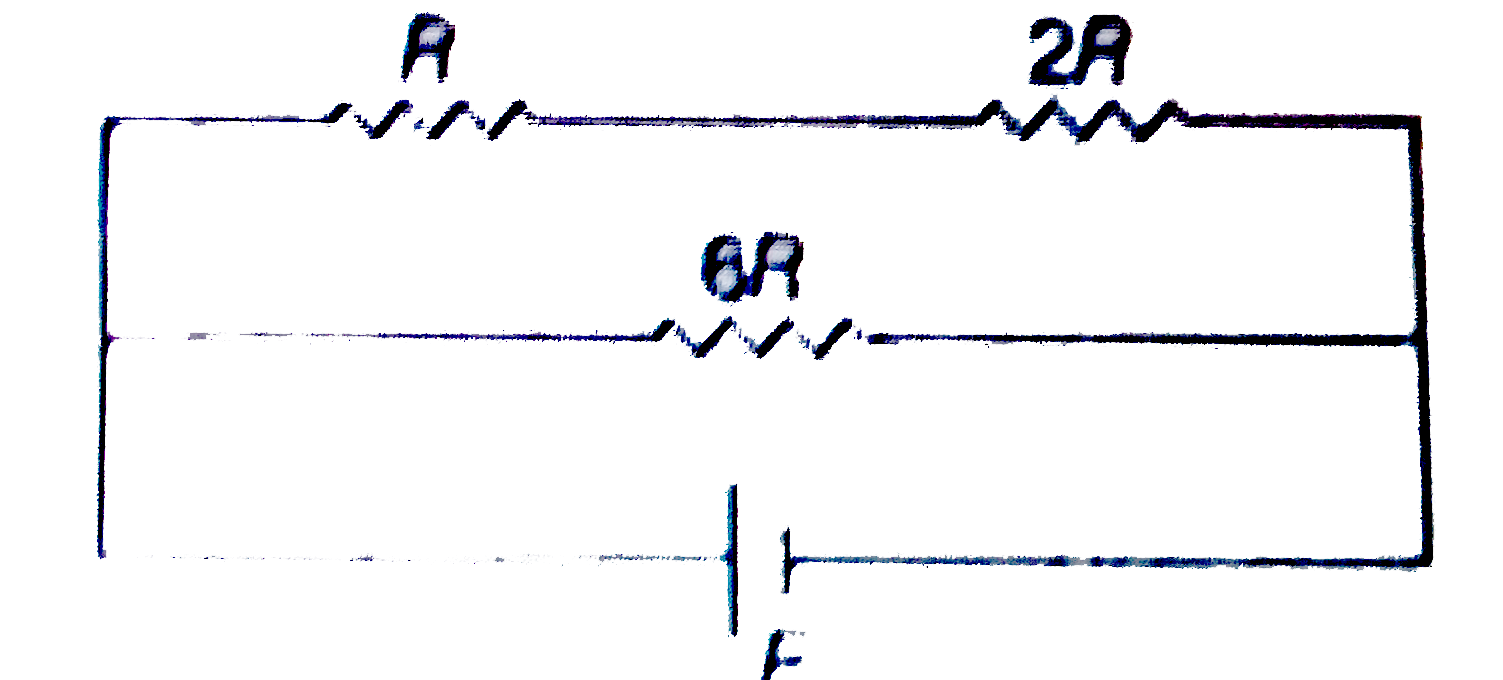
View SolutionA battery of emf 2 V and initial resistance 1Ω is
connected across terminals A and B of the circuit shown
in figure
 .
.
View SolutionA cell of emf ε and internal resistance r is connected across a load resistance R .
(i) Find the maximum power delivered at the load ?
(ii) Draw the power (P) vs load resistance (R) graph .
View Solution
