Two loudspeakers S1 and S2 each emit sounds of frequency 220HZ uniformly in all directions. S1 has an acoustic output of 1.2×10−3W and S2 has 1.8×10−3W . S1 and S2 vibrate in phase.Consider a point P such that S1P=0.75m and S2p=3m . How are the phases arriving at P related? What is the intensity at P when both S1 and S2 are on ? Speed of sound in air is 330m/s.
To solve the problem step by step, we will follow these steps:
Step 1: Calculate the wavelength (λ)
Given:
- Speed of sound (v) = 330 m/s
- Frequency (f) = 220 Hz
Using the formula:
λ=vf
Substituting the values:
λ=330m/s220Hz=1.5m
Step 2: Calculate the phase difference (Δφ) for S1 and S2
For S1:
- Distance from S1 to P (S1P) = 0.75 m
Using the formula for phase difference:
Δϕ=2πλ⋅Δx
Substituting for S1:
ΔϕS1=2π1.5⋅0.75=5radians
For S2:
- Distance from S2 to P (S2P) = 3 m
Substituting for S2:
ΔϕS2=2π1.5⋅3=4πradians
Step 3: Determine the phase difference between S1 and S2
Since both speakers vibrate in phase, the phase difference (Δφ) at point P is:
Δϕ=ΔϕS2−ΔϕS1=4π−5
Step 4: Calculate the intensity (I) at point P
The intensity (I) is given by:
I=P4πr2
For S1:
- Power (P1) = 1.2×10−3W
I1=1.2×10−34π(0.75)2=6.97×10−5W/m2
For S2:
- Power (P2) = 1.8×10−3W
I2=1.8×10−34π(3)2=1.59×10−5W/m2
Step 5: Calculate the resultant intensity at point P
The resultant intensity when both sources are on can be calculated using:
Iresultant=I1+I2+2√I1I2cos(Δϕ)
Since the speakers are in phase, cos(Δϕ)=1:
Iresultant=I1+I2+2√I1I2
Calculating:
Iresultant=6.97×10−5+1.59×10−5+2√(6.97×10−5)(1.59×10−5)
Calculating the last term:
2√(6.97×10−5)(1.59×10−5)=2×3.54×10−5=7.08×10−5
Thus:
Iresultant=6.97×10−5+1.59×10−5+7.08×10−5=8.24×10−5W/m2
Final Result
The resultant intensity at point P when both S1 and S2 are on is:
Iresultant=8.24×10−5W/m2
---
Given:
- Speed of sound (v) = 330 m/s
- Frequency (f) = 220 Hz
λ=vf
Substituting the values:
λ=330m/s220Hz=1.5m
For S1:
- Distance from S1 to P (S1P) = 0.75 m
Δϕ=2πλ⋅Δx
Substituting for S1:
ΔϕS1=2π1.5⋅0.75=5radians
- Distance from S2 to P (S2P) = 3 m
ΔϕS2=2π1.5⋅3=4πradians
Since both speakers vibrate in phase, the phase difference (Δφ) at point P is:
Δϕ=ΔϕS2−ΔϕS1=4π−5
The intensity (I) is given by:
I=P4πr2
- Power (P1) = 1.2×10−3W
I1=1.2×10−34π(0.75)2=6.97×10−5W/m2
- Power (P2) = 1.8×10−3W
I2=1.8×10−34π(3)2=1.59×10−5W/m2
The resultant intensity when both sources are on can be calculated using:
Iresultant=I1+I2+2√I1I2cos(Δϕ)
Iresultant=I1+I2+2√I1I2
Iresultant=6.97×10−5+1.59×10−5+2√(6.97×10−5)(1.59×10−5)
2√(6.97×10−5)(1.59×10−5)=2×3.54×10−5=7.08×10−5
Iresultant=6.97×10−5+1.59×10−5+7.08×10−5=8.24×10−5W/m2
The resultant intensity at point P when both S1 and S2 are on is:
Iresultant=8.24×10−5W/m2
Topper's Solved these Questions
- SOUND WAVESBook:DC PANDEY ENGLISHChapter:SOUND WAVESExercise:Subjective Questions
Explore 1 Video
- SOUND WAVESBook:DC PANDEY ENGLISHChapter:SOUND WAVESExercise:Level 2 Single Correct
Explore 14 Videos
- SOUND WAVESBook:DC PANDEY ENGLISHChapter:SOUND WAVESExercise:Level 1 Objective
Explore 34 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBook:DC PANDEY ENGLISHChapter:SOLVD PAPERS 2017 NEET, AIIMS & JIPMERExercise:Solved paper 2018(JIPMER)
Explore 38 Videos
- SUPERPOSITION OF WAVESBook:DC PANDEY ENGLISHChapter:SUPERPOSITION OF WAVESExercise:Level 2 Subjective
Explore 8 Videos
Similar Questions
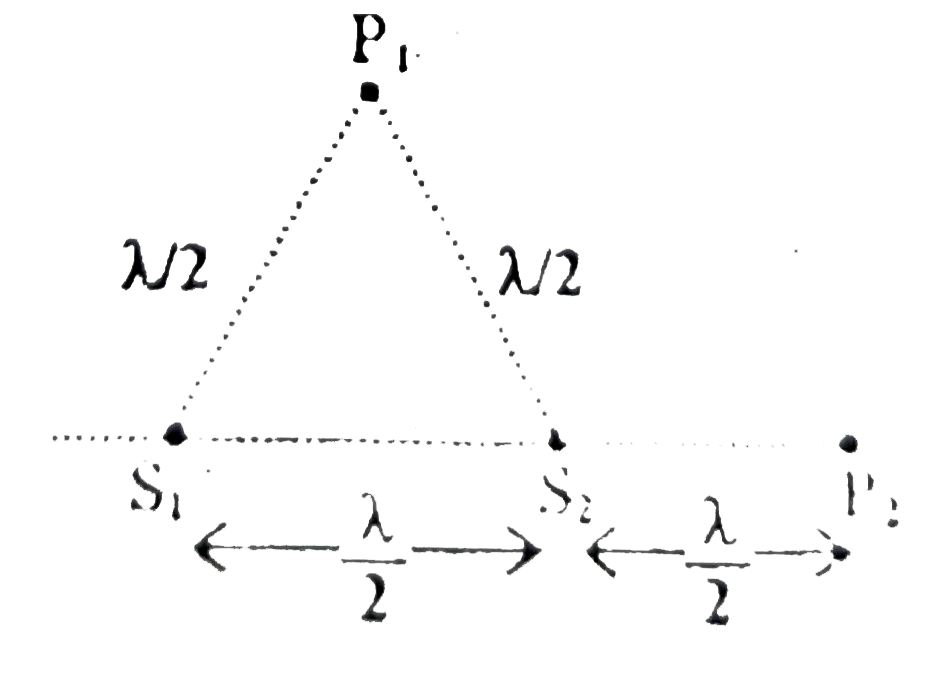
S1 and S2 are two equally intense coherent point second sources vibrating in phase. The resultant intensity at P1 is 80SI units then resultant intensity at P2 in SI units will be
View Solution_E01_054_Q01.png)
A monochromatic light source of wavelength λ is placed at S. three slits S1,S2 and S3 are equidistant from the source S and the point P on the screen S1P−S2P=λ/6 and S1P−S3P=2λ/3. if I be the intensity at P when only one slit is open the intensity at P when all the three slits are open is-
View Solution
Knowledge Check
In the case of light waves from two coherent sources S1 and S2, there will be constructive interference at an arbitrary point P, the path difference S1P−S2P is
A(n+12)λBnλC(n−12)λDλ2
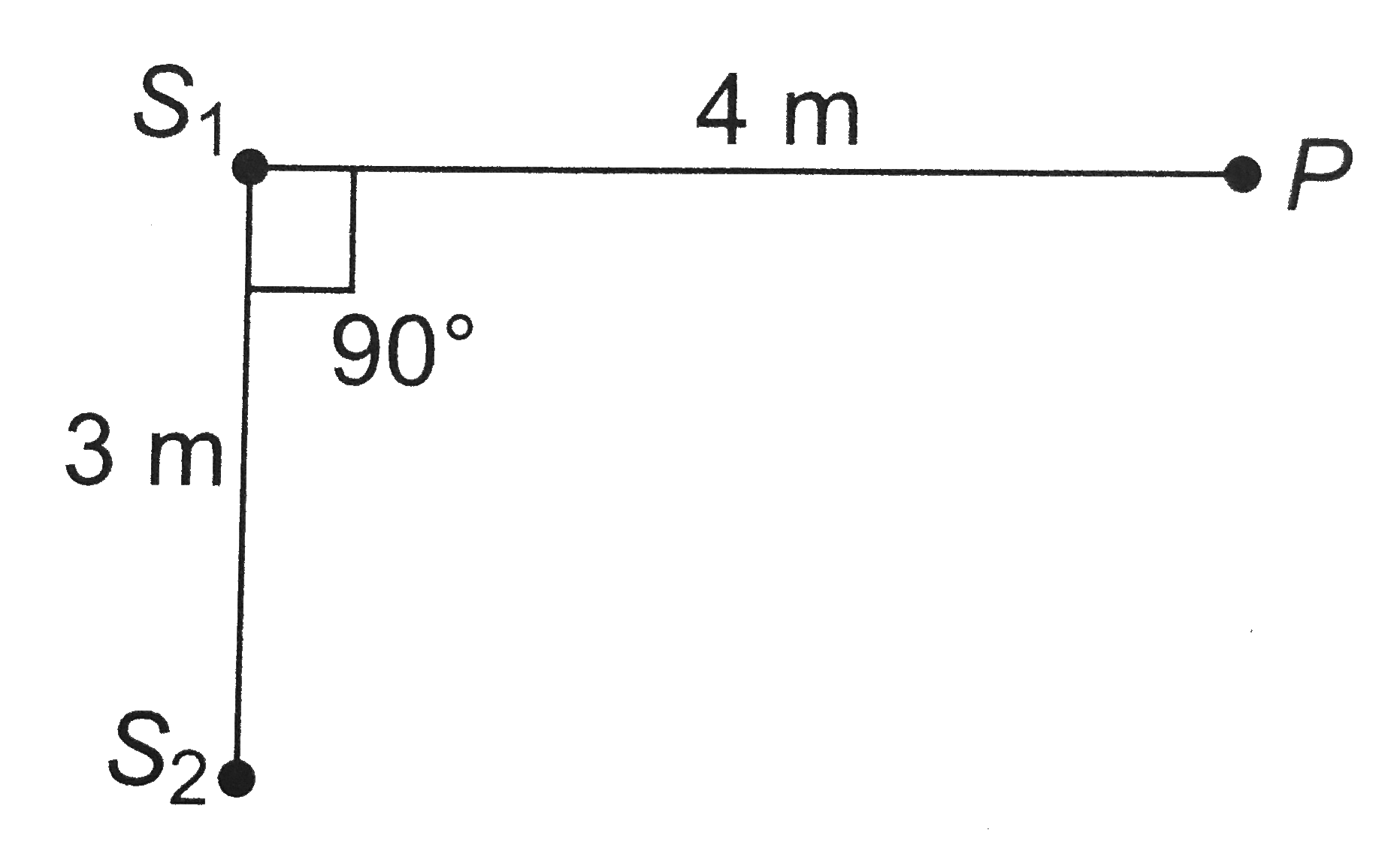
S1 and S2 are two coherent sources of sound of frequency 110Hz each they have no initial phase difference. The intensity at a point P due to S1 is I0 and due to S2 is 4I0. If the velocity of sound is 330m/s then the resultant intensity at P is
View SolutionTwo identical sounds s1ands2 reach at a point P phase. The resultant loudness at a point P is not higher than the loudness of s1. The value of n is
View SolutionTwo SHMs s1=asinωt and s2=bsinωt are superimposed on a particle. The s1 and s2 are along the direction which makes 37∘ to each other
View SolutionAmong two interfering sources, let S1 be ahead of the phase by 90∘ relative to S2 . If an observation point P is such that PS1−PS2=1.5λ , the phase difference between the waves from S1andS2 reaching P is
View SolutionA solution contains 0.10MH2Sand0.3HCl Calculate the concentration of S2−andHS− ions in the solution . For H2S,Ka1=1×10−7andKa2=1.3×10−13
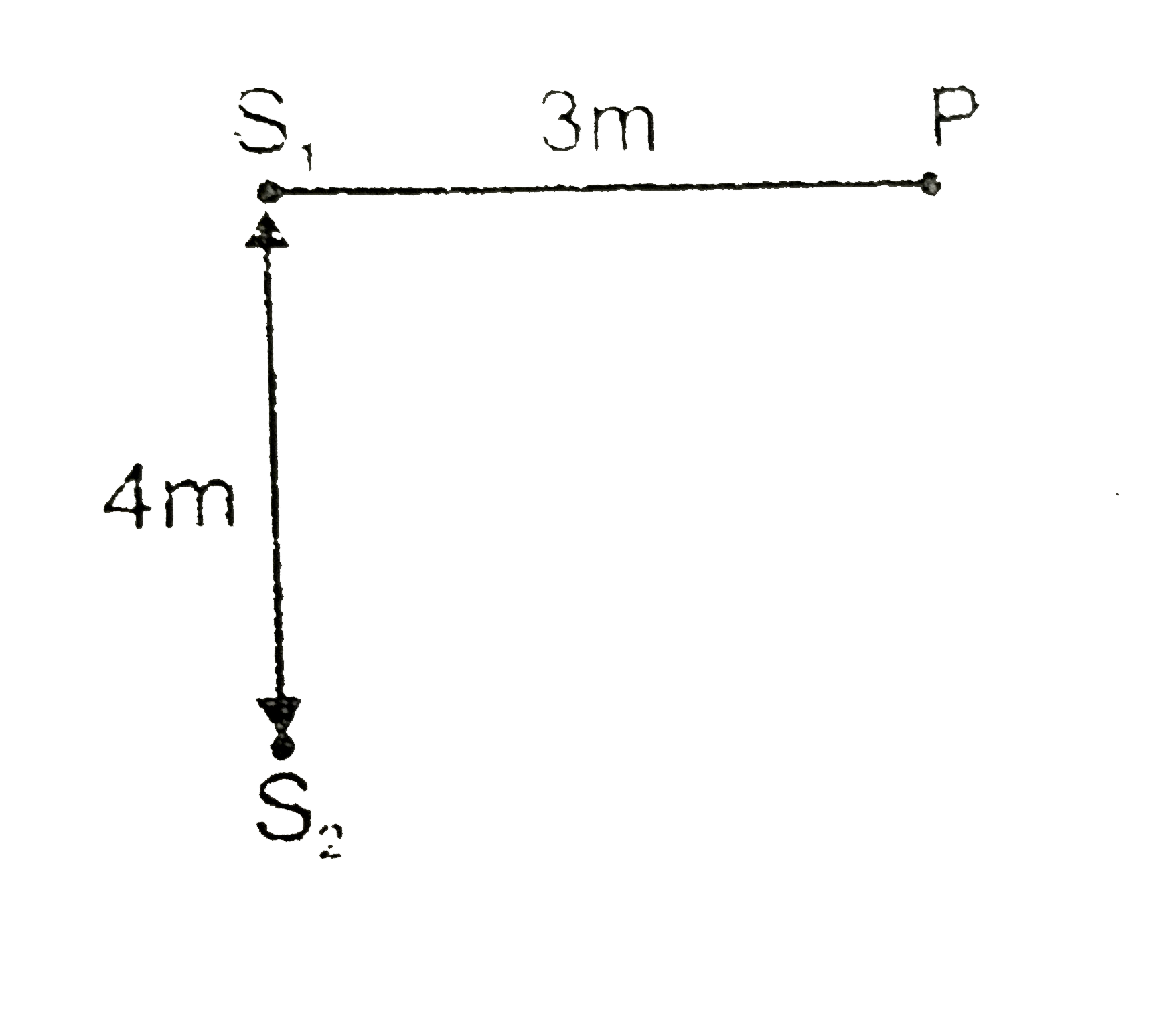
View SolutionS1 and S2 are two coherent sources of frequency f each.(θ1=θ2=0∘)Vsound=330m/s.
(i) so that constructive interfence at 'p'
(ii) so that destructive interfrece at 'p'
View SolutionK1andK2 ofH2S are 10−3and10−12 respectively what is [S−2] in 0.1 M H2 S buffered at p(H) =2
View Solution