Assertion : A particle is under SHM along the x - axis. Its mean position is , amplitude is and angular frequency . At , particle is at origin, then - co-ordinate versus time equation of the particle will be .
Reason : At , particle is at rest.
Both Assertion and Reason are true and the Reason is correct explanation of the Assertion.
Both Assertion and Reason are true but Reason is not the correct explanation of Assertion.
Assertion is true, but the Reason is false.
Assertion is false but the Reason is true.
The correct Answer is:B
To solve the problem, we need to analyze both the assertion and the reason provided in the question regarding the simple harmonic motion (SHM) of a particle.
1. Understanding the Assertion:
- The assertion states that a particle is undergoing SHM along the x-axis with a mean position at x=2, an amplitude A=2, and an angular frequency ω. At t=0, the particle is at the origin (x=0).
2. Formulating the SHM Equation:
- The general equation for SHM can be expressed as:
x(t)=Acos(ωt+ϕ)+k
where k is the mean position, A is the amplitude, and ϕ is the phase constant.
- Here, k=2 (mean position) and A=2 (amplitude).
3. Setting Up the Equation:
- Substituting the values into the SHM equation:
x(t)=2cos(ωt+ϕ)+2
4. Finding the Phase Constant:
- At t=0, the particle is at the origin (x=0):
0=2cos(ϕ)+2
- Rearranging gives:
2cos(ϕ)=−2⟹cos(ϕ)=−1
- This implies ϕ=π.
5. Final Equation:
- Substituting ϕ=π back into the equation:
x(t)=2cos(ωt+π)+2
- Since cos(θ+π)=−cos(θ), we can rewrite this as:
x(t)=−2cos(ωt)+2
- This matches the assertion that x(t)=−2cos(ωt)+2.
6. Understanding the Reason:
- The reason states that at t=0, the particle is at rest.
- To check this, we need to find the velocity v(t):
v(t)=dxdt=ddt(−2cos(ωt)+2)=2ωsin(ωt)
- At t=0:
v(0)=2ωsin(0)=0
- This confirms that the particle is at rest at t=0.
7. Conclusion:
- Both the assertion and the reason are true. However, the reason does not correctly explain the assertion since the assertion is about the position of the particle, while the reason discusses its velocity.
Final Answer:
- The correct option is B: Both assertion and reason are true, but the reason is not the correct explanation of the assertion.
- The assertion states that a particle is undergoing SHM along the x-axis with a mean position at x=2, an amplitude A=2, and an angular frequency ω. At t=0, the particle is at the origin (x=0).
- The general equation for SHM can be expressed as:
x(t)=Acos(ωt+ϕ)+k
where k is the mean position, A is the amplitude, and ϕ is the phase constant.
- Here, k=2 (mean position) and A=2 (amplitude).
- Substituting the values into the SHM equation:
x(t)=2cos(ωt+ϕ)+2
- At t=0, the particle is at the origin (x=0):
0=2cos(ϕ)+2
- Rearranging gives:
2cos(ϕ)=−2⟹cos(ϕ)=−1
- This implies ϕ=π.
- Substituting ϕ=π back into the equation:
x(t)=2cos(ωt+π)+2
- Since cos(θ+π)=−cos(θ), we can rewrite this as:
x(t)=−2cos(ωt)+2
- This matches the assertion that x(t)=−2cos(ωt)+2.
- The reason states that at t=0, the particle is at rest.
- To check this, we need to find the velocity v(t):
v(t)=dxdt=ddt(−2cos(ωt)+2)=2ωsin(ωt)
- At t=0:
v(0)=2ωsin(0)=0
- This confirms that the particle is at rest at t=0.
- Both the assertion and the reason are true. However, the reason does not correctly explain the assertion since the assertion is about the position of the particle, while the reason discusses its velocity.
- The correct option is B: Both assertion and reason are true, but the reason is not the correct explanation of the assertion.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBook:DC PANDEY ENGLISHChapter:SIMPLE HARMONIC MOTIONExercise:Level 1 Single Correct
Explore 24 Videos
- SIMPLE HARMONIC MOTIONBook:DC PANDEY ENGLISHChapter:SIMPLE HARMONIC MOTIONExercise:Level 1 Subjective
Explore 39 Videos
- SIMPLE HARMONIC MOTIONBook:DC PANDEY ENGLISHChapter:SIMPLE HARMONIC MOTIONExercise:Miscellaneous Examples
Explore 8 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBook:DC PANDEY ENGLISHChapter:SEMICONDUCTORS AND ELECTRONIC DEVICESExercise:More than One Option is Correct
Explore 3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBook:DC PANDEY ENGLISHChapter:SOLVD PAPERS 2017 NEET, AIIMS & JIPMERExercise:Solved paper 2018(JIPMER)
Explore 38 Videos
Similar Questions
The position vector of a particle is r=asinωtˆi+acosωtˆj
The velocity of the particle is
View SolutionA particle moves along the X-axis as x=u(t−2s)+a(t−2s)2.
View SolutionA particle moves along the X-axis as x=u(t−2s)=at(t−2)2.
View SolutionA particle moves along the x-axis according to the equation x=asinωt+bcosωt. The motion is simple harmonic with
View SolutionThe equation of motion of a particle is x=a cos(αt)2. The motion is
View SolutionTwo particles are in SHM with same amplitude A and same regualr frequency ω. At time t=0, one is at x =+A2 and the other is at x=−A2. Both are moving in the same direction.
View Solutionthe angular velocity omega of a particle varies with time t as ω=5t2+25rads. the angular acceleration of the particle att=1s is
View SolutionThe position x of a particle varies with time t as x=at2−bt3.The acceleration of the particle will be zero at time t equal to
View SolutionA particle is performing a motion on the x-axis with its position given by x=A+Bsinωt. The amplitude of particle is
View SolutionTwo particles are moving along x-axis. Their x-coordinate versus time graph are as shown below.
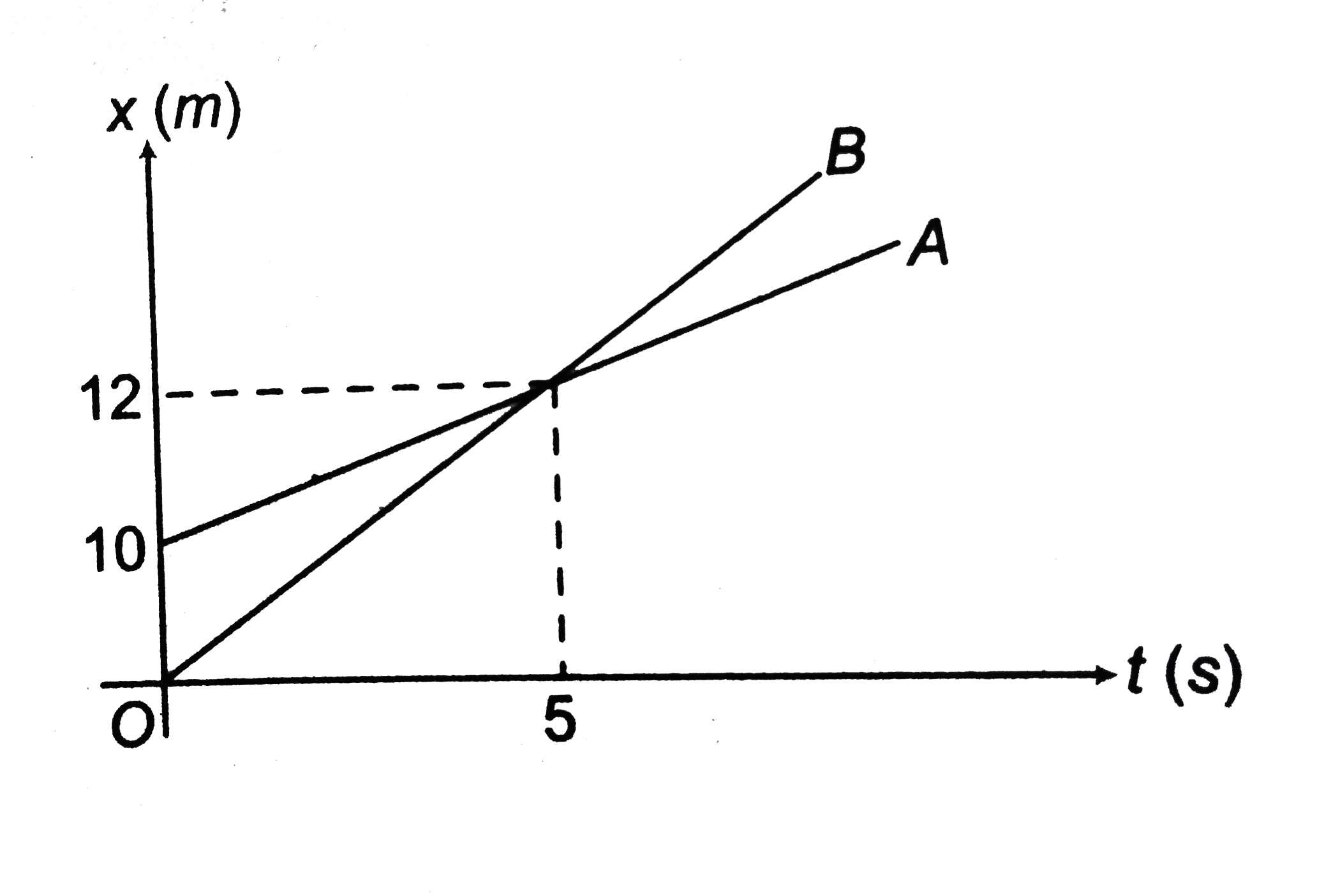
Find velocity of A w.r.t. B
View Solution