Consider a planet moving in an elliptical orbit round the sun. The work done on the planet by the gravitational force of the sun
To solve the problem of the work done on a planet moving in an elliptical orbit around the Sun by the gravitational force, we can follow these steps:
1. Understanding the Motion:
- The planet is moving in an elliptical orbit around the Sun. The points in the orbit where the planet is closest and farthest from the Sun are called perihelion and aphelion, respectively.
2. Identifying Forces:
- The gravitational force exerted by the Sun on the planet acts towards the Sun. This force changes direction as the planet moves along its elliptical path.
3. Work Done by Gravitational Force:
- Work done (W) by a force is given by the formula:
W=∫→F⋅d→s
- Here, →F is the gravitational force and d→s is the displacement of the planet.
4. Analyzing the Perpendicular Components:
- At certain points in the orbit, such as at perihelion, the gravitational force is perpendicular to the velocity of the planet. When the force is perpendicular to the displacement, the work done is given by:
W=F⋅ds⋅cos(90∘)=0
- Thus, at these points, the work done by the gravitational force is zero.
5. Considering the Entire Orbit:
- The gravitational force is a conservative force, meaning that the work done by this force over a closed path (the entire orbit) is zero. This is because the energy lost in one part of the orbit is regained in another part.
6. Conclusion:
- Therefore, the total work done on the planet by the gravitational force of the Sun as it completes one full orbit in an elliptical path is:
W=0
Final Answer:
The work done on the planet by the gravitational force of the Sun while it moves in an elliptical orbit is zero.
---
- The planet is moving in an elliptical orbit around the Sun. The points in the orbit where the planet is closest and farthest from the Sun are called perihelion and aphelion, respectively.
- The gravitational force exerted by the Sun on the planet acts towards the Sun. This force changes direction as the planet moves along its elliptical path.
- Work done (W) by a force is given by the formula:
W=∫→F⋅d→s
- Here, →F is the gravitational force and d→s is the displacement of the planet.
- At certain points in the orbit, such as at perihelion, the gravitational force is perpendicular to the velocity of the planet. When the force is perpendicular to the displacement, the work done is given by:
W=F⋅ds⋅cos(90∘)=0
- Thus, at these points, the work done by the gravitational force is zero.
- The gravitational force is a conservative force, meaning that the work done by this force over a closed path (the entire orbit) is zero. This is because the energy lost in one part of the orbit is regained in another part.
- Therefore, the total work done on the planet by the gravitational force of the Sun as it completes one full orbit in an elliptical path is:
W=0
The work done on the planet by the gravitational force of the Sun while it moves in an elliptical orbit is zero.
Topper's Solved these Questions
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Solved Examples
16 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Miscellaneous Examples
8 Videos
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE
10 Videos
Similar Questions
Knowledge Check
A planet revolves in elliptical orbit around the sun. (see figure). The linear speed of the planet will be maximum at
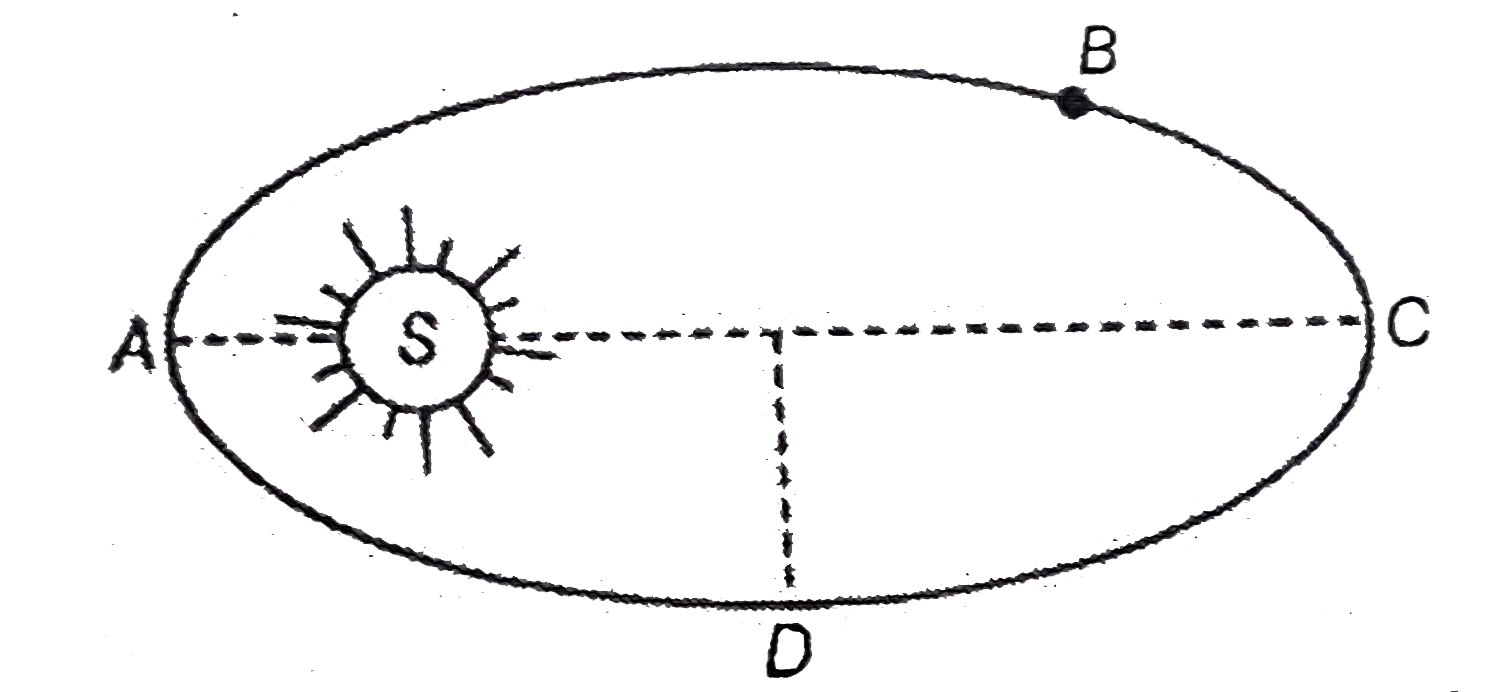 AABBCCDD
AABBCCDDA planet is revolving in an elliptical orbit around the sun. Its closest distance from the sun is r and the farthest distance is R. If the velocity of the planet nearest to the sun be v and that farthest away from the sun be V. then v/V is
AR2/r2Br2/R2CR/rDr/R
Statement-1:When a planet approches the point which is farthest from the sun, its orbital speed decreases.
Statement-2: Work done on the planet by the gravitational force exerted by the sun is negative.
View SolutionFigure shows a planet in an elliptical orbit around the Sun S. Where is the kinetic energy of the planet maximum?
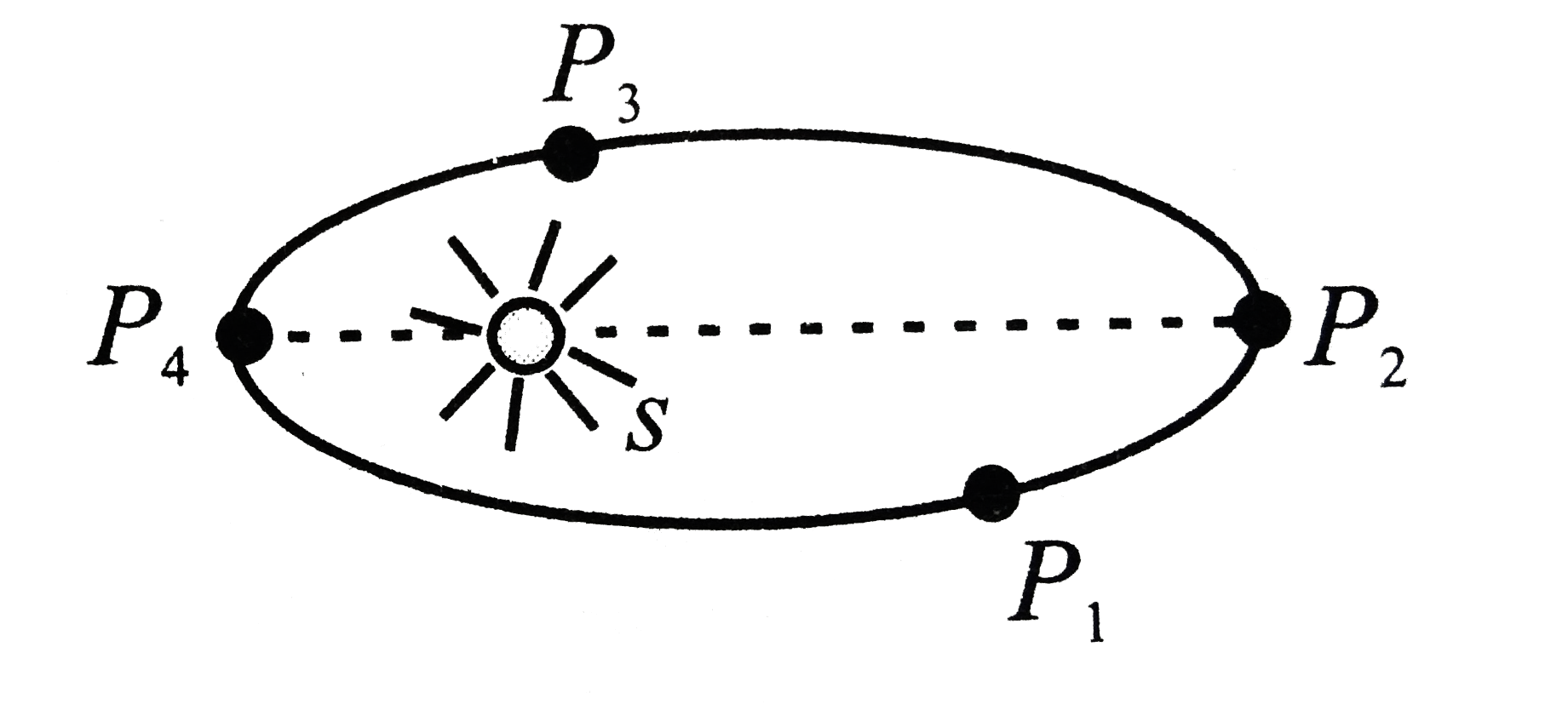
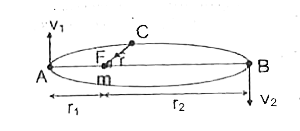
View SolutionIn the figure shown a planet moves in an elliptical orbit around the sun. Compare the speeds, linear and angular momenta at the points A and B.
View SolutionSTATEMENT -1 : When a planet revolves around Sun in an elliptical orbit, the work done Sun's gravitational force on the planet remains zero for any value of displacement.
and
STATEMENT -2 : The mechanical energy of Sun planet system remains conserved throughout the motion of planet.
View SolutionA planet revolves in elliptical orbit around the sun. (see figure). The linear speed of the planet will be maximum at

View SolutionA planet is revolving in an elliptical orbit around the sun as shown in the figure. The areal velocity (area swapped by the radius vector with respect to sun in unit time) is:
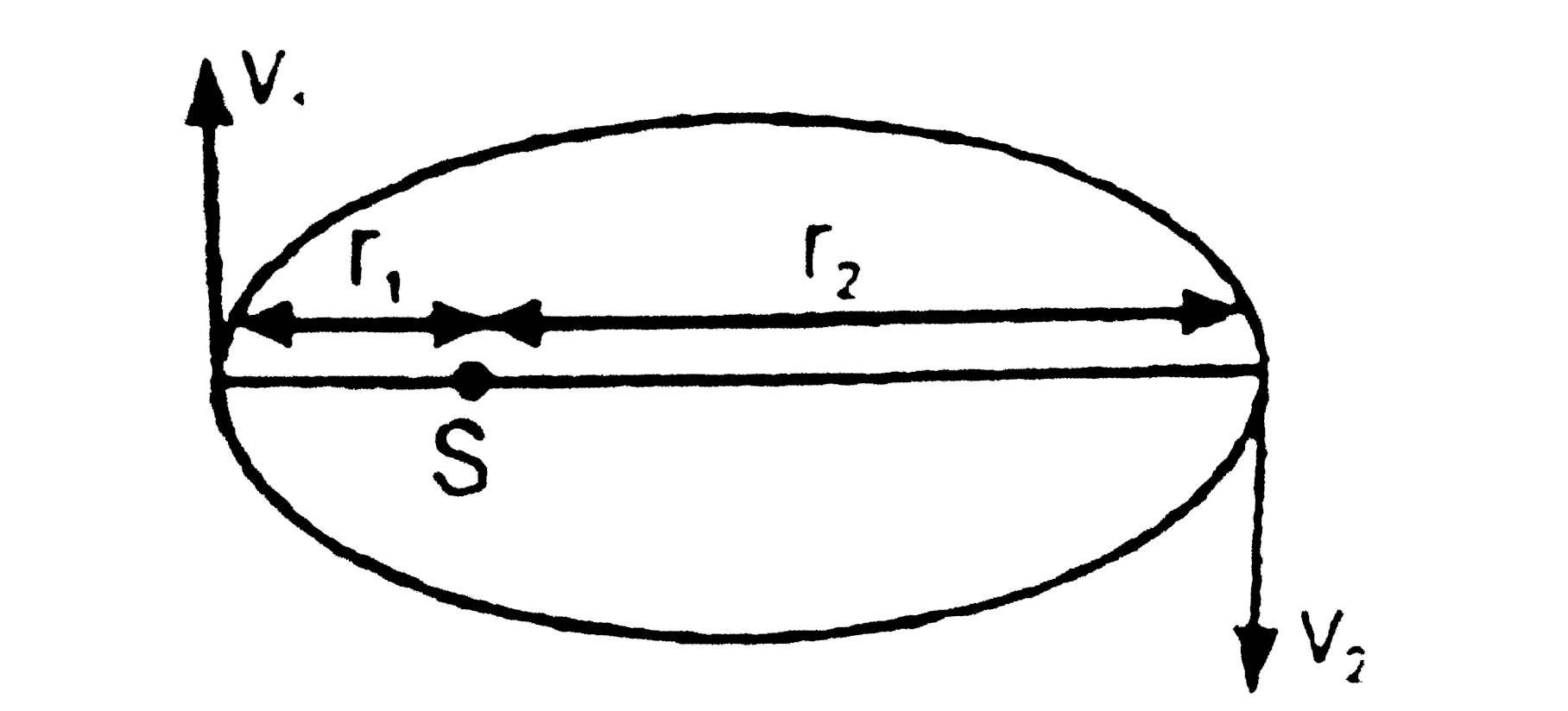
View Solution
