
Using the concept of instantaneous axis of rotation. Find speed of particle P as shown in figure, under pure rolling condition.
ωr
ωr2
2ωr
ω2r
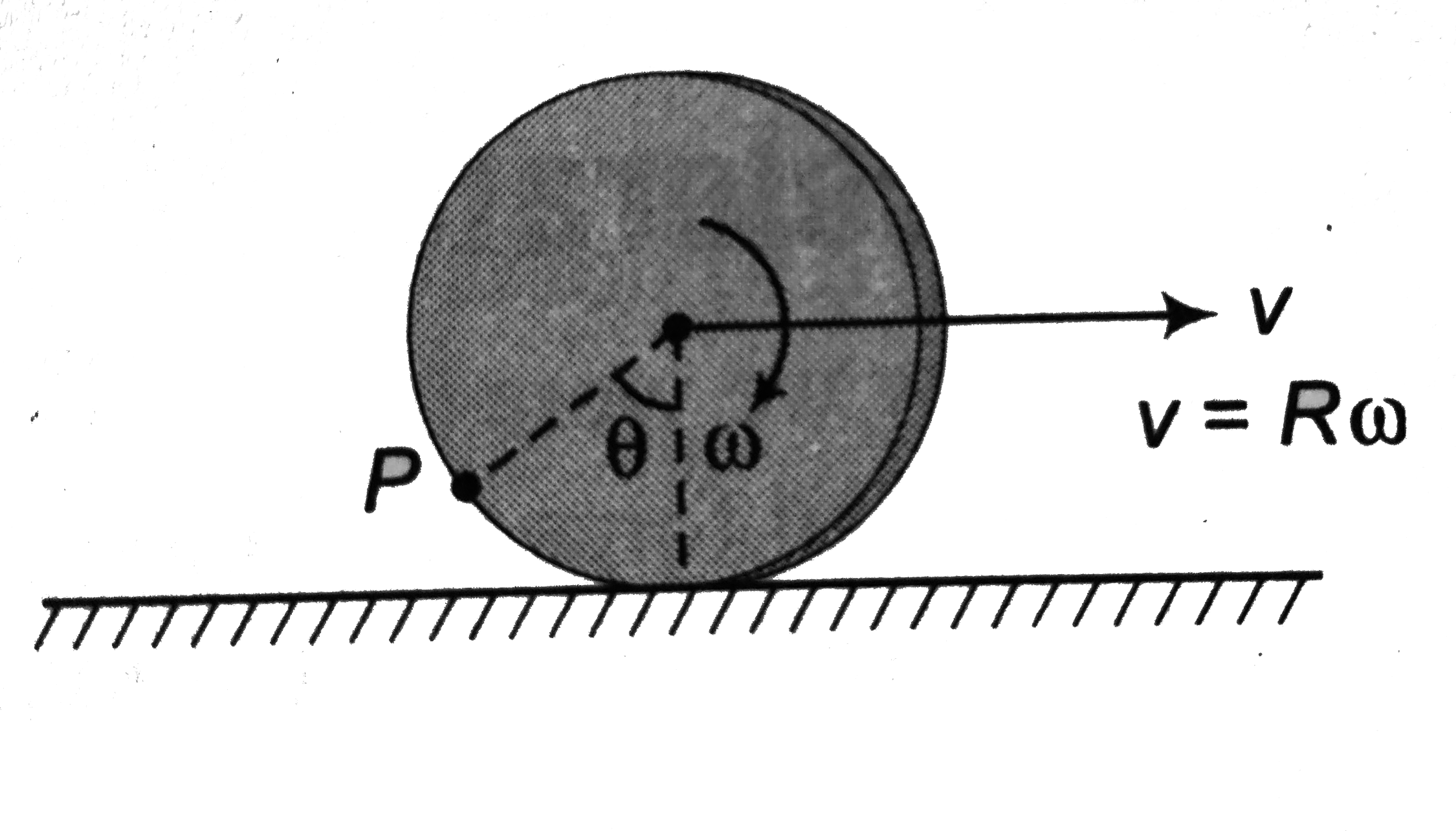
In pure rolling, combined rotation and translation motion may be assumed to be a pure rotational motion about an axis passing through bottommost point (with same ω) or instantaneous axis of rotation
|VP|=(OP)ω here OP=2Rsin(θ2)
therfore|VP|=(2Rsin(θ2)ω=2Rωsin(θ2)=2vsin(θ2)
Topper's Solved these Questions
- ROTATIONAL MECHANICSBook:DC PANDEY ENGLISHChapter:ROTATIONAL MECHANICSExercise:Solved Examples
Explore 25 Videos
- ROTATIONAL MECHANICSBook:DC PANDEY ENGLISHChapter:ROTATIONAL MECHANICSExercise:Miscellaneous Examples
Explore 2 Videos
- ROTATIONBook:DC PANDEY ENGLISHChapter:ROTATIONExercise:(C) Chapter Exercises
Explore 39 Videos
- ROTATIONAL MOTIONBook:DC PANDEY ENGLISHChapter:ROTATIONAL MOTIONExercise:Integer Type Questions
Explore 17 Videos
Similar Questions

A disc is rolling without slipping with linear velocity v as shown in figure. With the concept of instantaneous axis of rotation, find velocities of point A, B, C and D.
View SolutionA ring rotates about z axis as shown in figure. The plane of rotation is xy. At a certain instant the acceleration of a particle P (shown in figure) on the ring is (6ˆi−8ˆj)m/s2. Find the angular acceleration of the ring & the abgular velocity at that instant. Radius of the ring is 2m.

View SolutionFind the velocity of image of a moving particle O in the situation as shown in the figure.
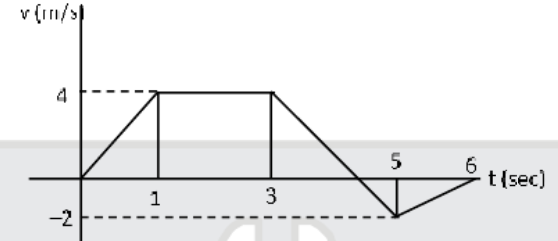
View Solutionvelocity time graph of a particle is shown in figure. Find displacement of the particle.
View SolutionFind the angular momentum of a disc about the axis shown in figure in the following situations.

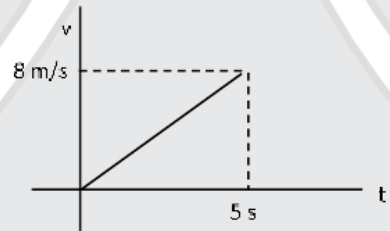
View SolutionSpeed time graph of a particle shown in figure. Find distance travelled by particle in 5second.
View SolutionFind the position of instantaneous centre of rotation and angular velocity of the disc in the following cases as shown. Radius of disc is R in each case.

View SolutionA particle is going in a spiral path as shown in figure with constant speed.
 .
.
View SolutionA liquid of density 'ρ' is rotated with an angular speed 'ω' as shown in figure. Using the pressure equation concept find the equation of free surface of the liquid.
 .
.
View SolutionAssertion : Speed of any point on rigid body executing rolling motion can be calculated by expression v=rω, where r is distance of point from instantaneous centre of rotation
Reason : Rolling motion of rigid body can be considered as a pure rotation about instantaneous centre of rotation.
View Solution

