A smooth chain (AB) of mass (m) rests against a surface in the form of a quarter of circle of radius R. If it is released from rest, the form of a quarter of a circle of radius R. If it is releaded from, the velocity of the chain after it comes over the horizontal part of the surface is .

(a)
(b)
(c)
(d)
The correct Answer is:C
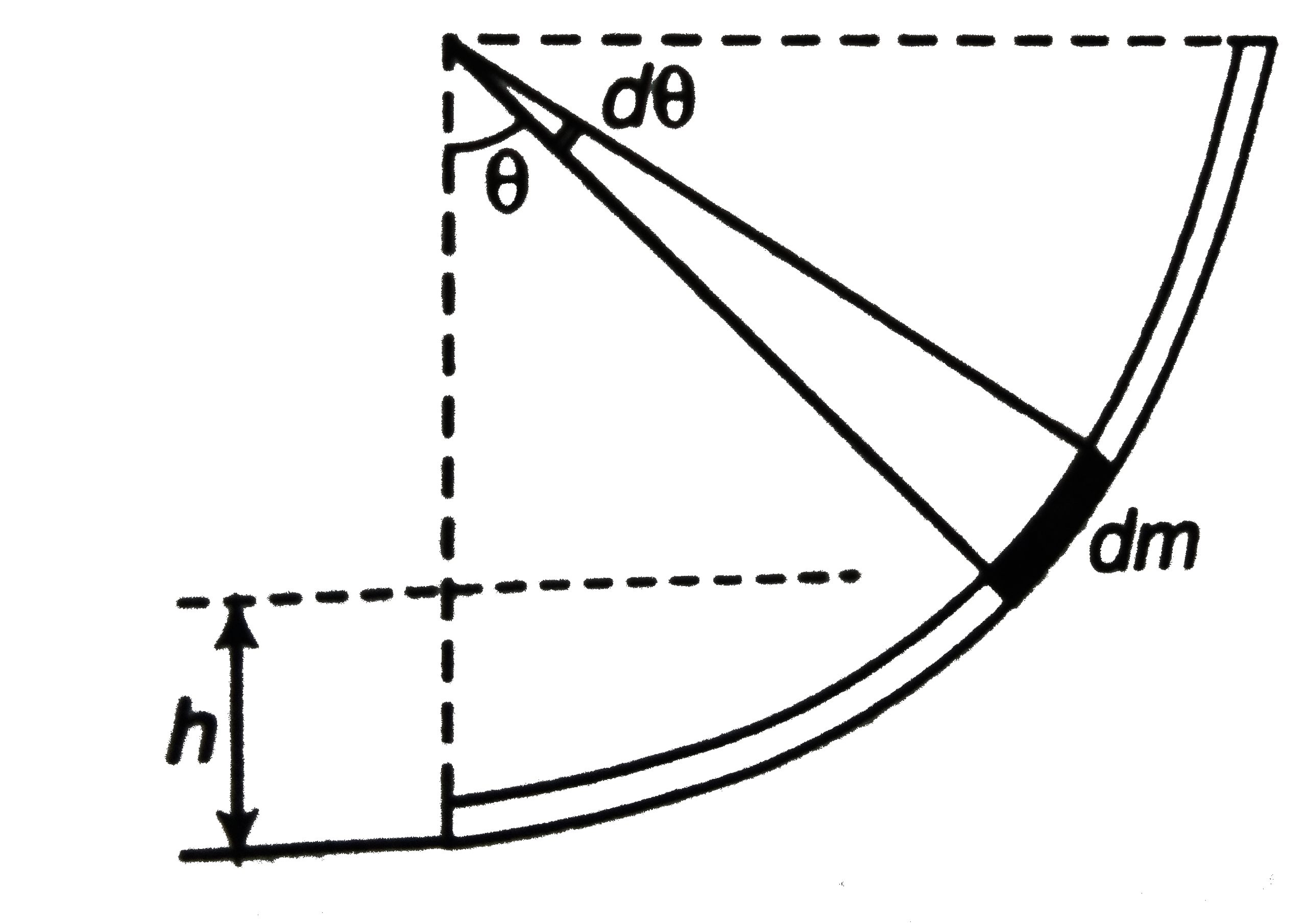
Now,
or
Topper's Solved these Questions
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 More Than One Correct
9 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Subjective
15 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 1 subjective
27 Videos
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Integer Type Question
11 Videos
- WORK, ENERGY AND POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRACES GALLERY
33 Videos
Similar Questions
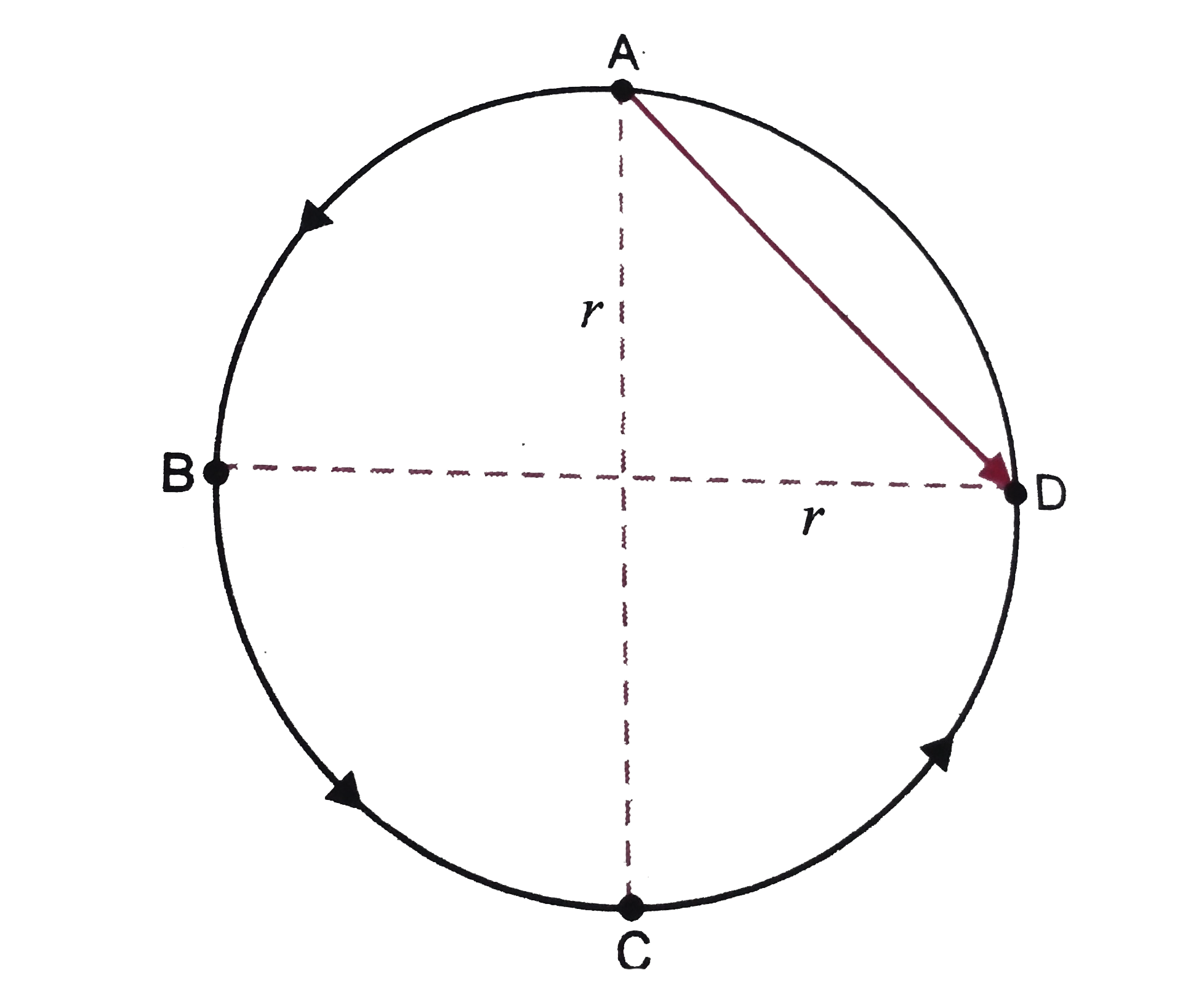
A particle moves over three quarters of a circle of radius r. What is the magnitude of its displacement ?
View SolutionA ball of mass m and radius r rolls inside a hemispherical shell of radius R. It is released from rest from point A as shown in figure. The angular velocity of centre of the ball in position B about the centre of the shell is.
 .
.
View SolutionA block of mass M with a semi - circular track of radius R rests on a smooth floor. A sphere of mass m and radius r is released from rest from A. Find the velocity of sphere and track , when the sphere reaches B.

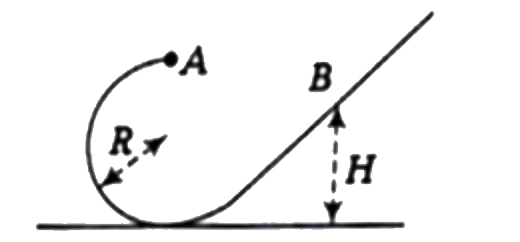
View SolutionA small bead of mass M slides on a smooth wire that is bent in a circle of radius R. It is released at the top of the circular part of the wire (point A in the figure) with a negligibly small velocity. Find the height H where the bead will reverse direction
View SolutionA chain of length l and mass m lies on the surface of a smooth sphere of radius R>l with one end tied to the top of the sphere.
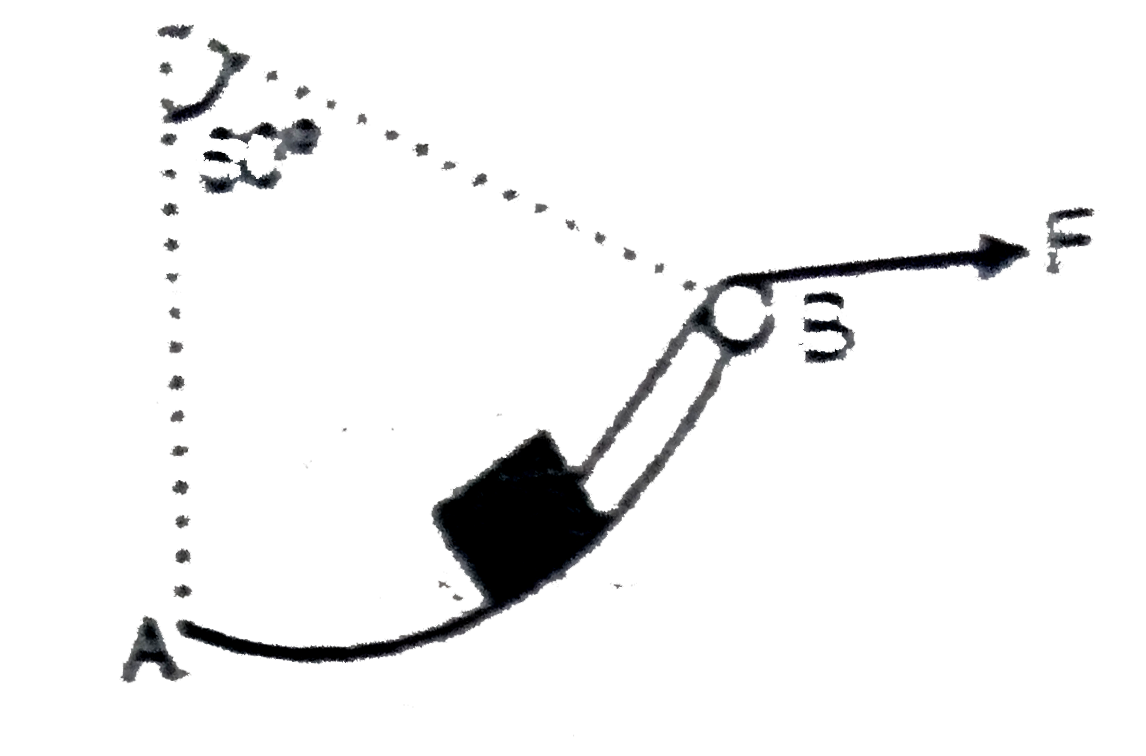
View SolutionA 10 kg block is pulled in the vertical plane along a frictionless surface in the form of an arc of a circle of radius 10m. The applied force is 200N as shown in the figure. If the block started from rest at A, the velocity at B would be:
View SolutionA particle of mass m is rigidly attached at A to a ring of mass 3m and radius r. The system is released from rest and rolls without sliding. The angular acceleration of ring just after release is

View SolutionIf O is the centre of a circle with radius r and AB is a chord of the circle at a distance r2 from O, then ∠BAO=
View SolutionThe radius of a planet is R. A satellite revolves around it in a circle of radius r with angular velocity ω0. The acceleration due to the gravity on planet's surface is
View SolutionA block of mass m is suspended from a pulley in form of a circular disc of mass m & radius R. The system is released from rest, find the angular velocity of disc when block has dropped by height h. (there is no slipping between string & pulley)
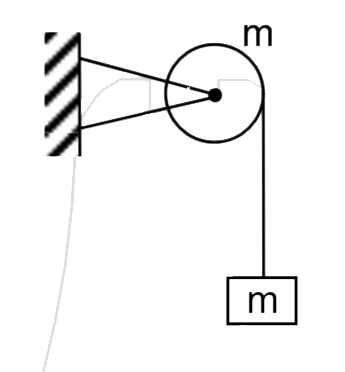
View Solution
