A rod of length 1.0m and mass 0.5kg fixed at ond is initially hanging vertical. The other end is now raised until it makes an angle 60∘ with the vertical. How much work is required?
The correct Answer is:A, B
To solve the problem of how much work is required to raise a rod of length 1.0 m and mass 0.5 kg from a vertical position to an angle of 60° with the vertical, we can follow these steps:
Step 1: Understand the Initial and Final Positions
- The rod is initially hanging vertically, which means its center of mass is at a height of L2 from the pivot point (the fixed end).
- When the rod is raised to an angle of 60° with the vertical, we need to determine the new height of the center of mass.
Step 2: Calculate the Height Change (ΔH)
- The center of mass of the rod is located at a distance of L2=1.02=0.5 m from the pivot.
- When the rod is raised to an angle of 60°, the vertical height of the center of mass can be found using trigonometry:
New height=L2cos(60°)=0.5⋅12=0.25 m
- The change in height (ΔH) is then:
ΔH=Initial height−New height=0.5 m−0.25 m=0.25 m
Step 3: Calculate the Work Done (W)
- The work done in raising the rod is equal to the change in potential energy, which can be calculated using the formula:
W=mgΔH
- Here, m=0.5 kg, g=10 m/s² (approximating the acceleration due to gravity), and ΔH=0.25 m.
- Substituting the values:
W=0.5⋅10⋅0.25=1.25 joules
Final Answer
The work required to raise the rod is 1.25 joules.
---
- The rod is initially hanging vertically, which means its center of mass is at a height of L2 from the pivot point (the fixed end).
- When the rod is raised to an angle of 60° with the vertical, we need to determine the new height of the center of mass.
- The center of mass of the rod is located at a distance of L2=1.02=0.5 m from the pivot.
- When the rod is raised to an angle of 60°, the vertical height of the center of mass can be found using trigonometry:
New height=L2cos(60°)=0.5⋅12=0.25 m
- The change in height (ΔH) is then:
ΔH=Initial height−New height=0.5 m−0.25 m=0.25 m
- The work done in raising the rod is equal to the change in potential energy, which can be calculated using the formula:
W=mgΔH
- Here, m=0.5 kg, g=10 m/s² (approximating the acceleration due to gravity), and ΔH=0.25 m.
- Substituting the values:
W=0.5⋅10⋅0.25=1.25 joules
The work required to raise the rod is 1.25 joules.
Similar Questions
A uniform rod of length L and mass M is pivoted freely at one end and placed in vertical position.
a. What is angular acceleration of the rod when it is at ann angle θ with the vertical?
b. What is the tangential linear acceleration of the free end when the rod is horizontal?
View SolutionA particle of mass 200 g , is whirled into a vertical circle of radius 80 cm uisig a massless string The speed of the particle when the string makes an angle of 60∘ with the vertical line is 1.5ms−1. The tension in the string at this position is
View Solution
Knowledge Check
A stone of mass m is tied to one end of a wire of length L. The diameter of the wire is D and it is suspended vertically. The stone is now rotated in a horizontal plane and makes an angle θ with the vertical. If Young's modulus of the wire is Y, Then the increase in the length of the wire is
A4mglπD2YB4mglπD2YsinθC4mglπD2YcosθD4mglπD2Ytanθ
A mass of M kg is suspended by a weightless string. The horizontal force required to displace it until string makes an angle of 45∘ with the initial vertical direction is:
View SolutionA uniform ladder of length 10.0 m and mass 16.0 kg is resting against a vertical smooth wall making an angle of 37∘ with it. An electrian weighing 60.0 kg climbs up the ladder. If the stays on the ladder at a point 8.00 m from the lower end, what will be normal force and the force of friction on the ladder by the ground? What should be the minimum coefficient of friction for the electrician to work safely?
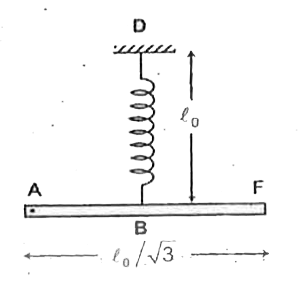
View SolutionIn the figure shown one end of a light spring of natural length l0=√58m(≈0.8m) is fixed at point D and other end is attached to the centre B of a uniform rod AF of length l0/√3 and mass 10kg. The rod is free to rotate in a vertical plane about a fixed horizontal axis passing through the end A of the rod. The rod is held at rest in horizontal position and the spring is in relaxed state. It is found that, when the rod is released to move it makes an angle of 60∘ with the horizontal when it comes to rest for the first time. Find the
(a) the maximum elogation in the spring . (Approximately)
(b) the spring constant. (Approximately)
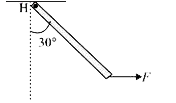
View SolutionA rod of mass m and length L is hinged at its top end. If the rod is in equilibrium making an angle of 30∘ with the vertical when a horizontal force F is applied as shown in figure, then the value of F is:
View SolutionA thin uniform rod of length l and mass m is freely pivoted about its end. The rod is initially held horizontally and released from rest. When the rod is vertical, an impulse J is applied to bring it to rest (this is in addition to any impulse provided by the pivot)

What is the angular velocity of the rod at the moment it reaches the vertical position ?
View SolutionAn object of mass 10kg is connected to the lower end of a massless string of length 4m hanging from the ceiling. If a force F is applied horizontally at the mid-point of the string, the top half of the string makes an angle of 45∘ with the vertical , then the magnitude of F is
View SolutionA mass of 10 kg is suspended from a spring balance. It is pulled aside by a horizontal string so that it makes an angle of 60∘ with the vertical. The new rading of the balance is
View Solution

