A lift a mass 1200kg is raised from rest by a cable with a tension 1350kgf . After same time the tension drops to 1000kgf and the lift comes to rest at a height of 25m above its intial point (1kg−f=9.8N)
What is the greatest speed of lift?
9.8ms−1
7.5ms−1
5.92ms−1
None of these
The correct Answer is:C
To solve the problem step by step, we will analyze the motion of the lift in two phases: the acceleration phase and the deceleration phase.
Step 1: Calculate the acceleration when the tension is 1350 kgf
1. Convert the tension from kgf to Newtons:
T1=1350kgf×9.8N/kgf=13230N
2. Calculate the weight of the lift:
W=m⋅g=1200kg×9.8N/kg=11760N
3. Determine the net force acting on the lift:
Fnet=T1−W=13230N−11760N=1470N
4. Calculate the acceleration using Newton's second law:
a1=Fnetm=1470N1200kg=1.225m/s2
Step 2: Calculate the distance traveled during acceleration
1. Use the kinematic equation to find the distance (h1) during acceleration:
Since the lift starts from rest, we can use the formula:
h1=12a1t2
We will need to find the time (t) later.
Step 3: Calculate the deceleration when the tension drops to 1000 kgf
1. Convert the tension from kgf to Newtons:
T2=1000kgf×9.8N/kgf=9800N
2. Determine the net force during deceleration:
Fnet=T2−W=9800N−11760N=−1960N
3. Calculate the deceleration:
a2=Fnetm=−1960N1200kg=−1.6333m/s2
Step 4: Calculate the distance traveled during deceleration (h2)
1. The total height the lift travels is 25 m:
h1+h2=25m
2. Using the kinematic equation for deceleration:
v2=u2+2a2h2
where u is the maximum speed reached at the end of the acceleration phase.
Step 5: Relate the maximum speed to the distances and accelerations
1. Using the relationship:
v2=2a1h1=−2a2h2
2. From the previous steps, we can express h2 in terms of h1:
h2=25−h1
Step 6: Solve for maximum speed (v)
1. Substituting the values:
v2=2⋅1.225⋅h1=−2⋅(−1.6333)⋅(25−h1)
2. Solving the equations simultaneously will give us the maximum speed:
After calculations, we find:
v=5.92m/s
Final Answer
The greatest speed of the lift is 5.92m/s.
---
T1=1350kgf×9.8N/kgf=13230N
W=m⋅g=1200kg×9.8N/kg=11760N
Fnet=T1−W=13230N−11760N=1470N
a1=Fnetm=1470N1200kg=1.225m/s2
Since the lift starts from rest, we can use the formula:
h1=12a1t2
We will need to find the time (t) later.
T2=1000kgf×9.8N/kgf=9800N
Fnet=T2−W=9800N−11760N=−1960N
a2=Fnetm=−1960N1200kg=−1.6333m/s2
h1+h2=25m
v2=u2+2a2h2
where u is the maximum speed reached at the end of the acceleration phase.
v2=2a1h1=−2a2h2
h2=25−h1
v2=2⋅1.225⋅h1=−2⋅(−1.6333)⋅(25−h1)
After calculations, we find:
v=5.92m/s
The greatest speed of the lift is 5.92m/s.
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Subjective Question
27 Videos
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Check point 5.1
20 Videos
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Objective Question
32 Videos
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
- LAWS OF THERMODYNAMICSBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Subjective
18 Videos
Similar Questions
A lift a mass 1200kg is raised from rest by a cable with a tension 1350kgf . After same time the tension drops to 1000kgf and the lift comes to rest at a height of 25m above its intial point (1kg−f=9.8N)
What is the height at which the tension changes ?
View SolutionA lift starts from rest. Its acceleration is plotted against time. When it comes to rest its height above its starting point is
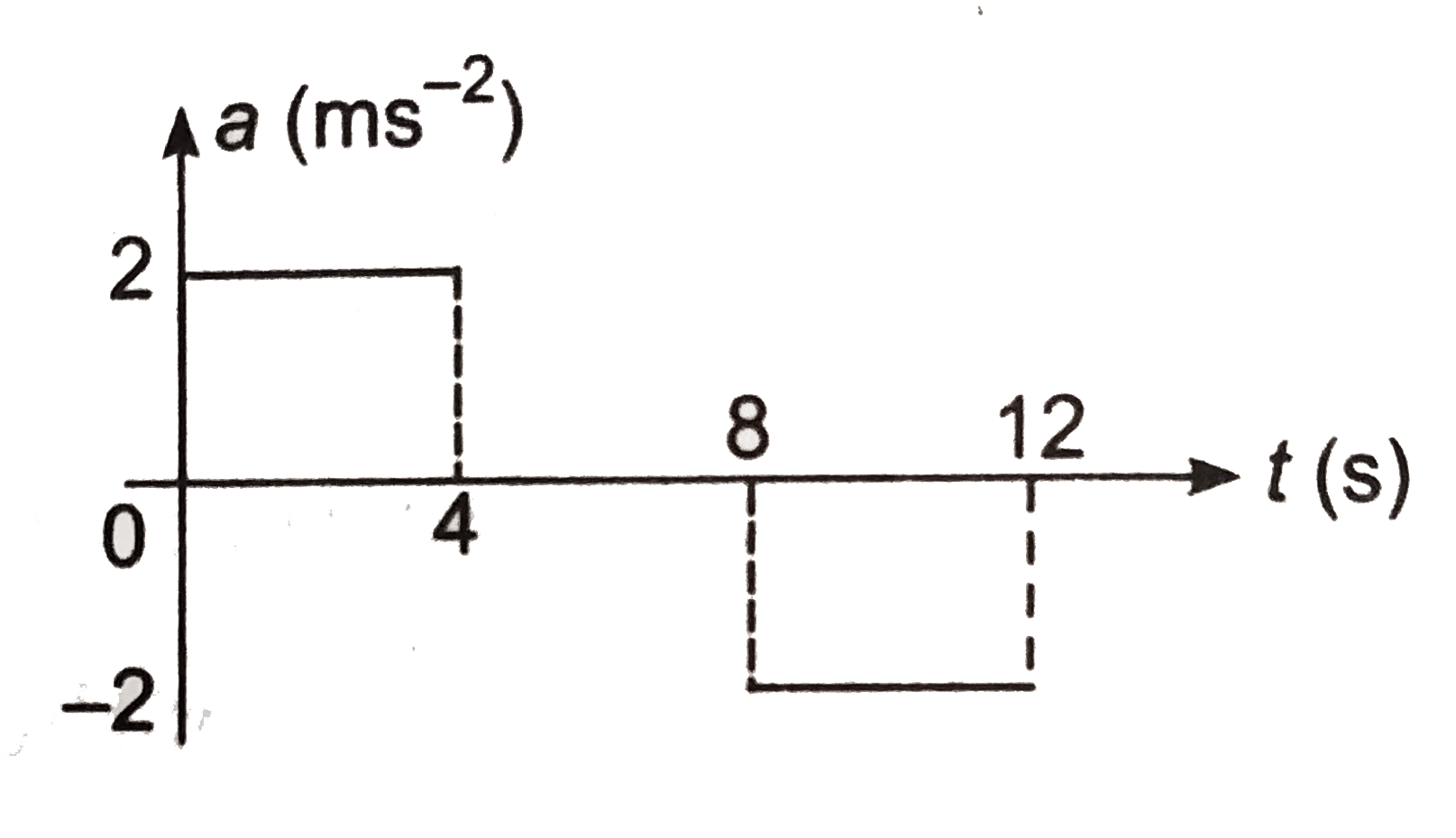
View Solution
Knowledge Check
If a body of mass 5 kg is lifted from the ground level to a height of 5m then ratio of its inertia is …………..
A1:1BsameCconstantDnot defined
A particle of mass 1 kg is released from rest at a point where gravitational potential is 5 J/kg. After some time, it passes through a point B with a speed of 1 m/s. What is the gravitational potential at B ?
View SolutionA lift of mass 100 kg is moving upwards with an acceleration of 1 m/s2. The tension developed in the string, which is connected to lift is (g=9.8m/s2)
View SolutionA block of mass √2 kg is released from the top of an inclined smooth surface as shown in fighre. If spring constant of spring is 100 N/m and block comes to rest after compressing the spring by 1 m, then the distance travelled by block befor it comes to rest is

View SolutionA block of mass √2 kg is released from the top of an inclined smooth surface as shown in fighre. If spring constant of spring is 100 N/m and block comes to rest after compressing the spring by 1 m, then the distance travelled by block befor it comes to rest is

View SolutionA lift of mass 1000kg is moving with an acceleration of 1m/s2 in upward direction. Tension developed in the string, which is connected to the lift, is.
View SolutionA lift of mass 1000kg is moving with an acceleration of 1m/s2 in upward direction. Tension developed in the string, which is connected to the lift, is.
View SolutionA 1000 kg lift is supported by a cable that can support 2000 kg. The shortest distance in which the lift can be stopped when it is descending with a speed of 2.5m/s is (g=10m/s2)
View Solution
