In the above example, if two blocks have masses 1kg and 2kg respectively then find their acceleration and tension in different string.
To solve the problem of finding the acceleration and tension in the strings for two blocks with masses of 1 kg and 2 kg, we will follow these steps:
1. Identify the Forces Acting on Each Block:
- For Block 1 (mass = 1 kg):
- Weight (downward force) = W1=m1⋅g=1⋅10=10N
- Tension in the strings acting upward = T1=4T (from the video)
- For Block 2 (mass = 2 kg):
- Weight (downward force) = W2=m2⋅g=2⋅10=20N
- Tension in the strings acting upward = T2=T
2. Write the Equations of Motion:
- For Block 1 (upward direction is positive):
4T−10=1⋅a(Equation 1)
- For Block 2 (downward direction is positive):
20−T=2⋅(7a)(Equation 2)
3. Simplify the Equations:
- From Equation 1:
4T−10=a⇒a=4T−10(1)
- From Equation 2:
20−T=14a⇒T=20−14a(2)
4. Substitute Equation (1) into Equation (2):
- Substitute a=4T−10 into T=20−14a:
T=20−14(4T−10)
T=20−56T+140
57T=160⇒T=16057≈2.81N
5. Calculate the Acceleration a:
- Substitute T back into Equation (1):
a=4T−10=4⋅16057−10
a=64057−10=64057−57057=7057≈1.23m/s2
6. Calculate the Tensions in Each String:
- Tension in String 1:
T1=4T=4⋅16057≈11.24N
- Tension in String 2:
T2=2T=2⋅16057≈5.62N
- Tension in String 3:
T3=T≈2.81N
Final Answers:
- Acceleration of Block 1: a≈1.23m/s2 (upward)
- Tension in String 1: T1≈11.24N
- Tension in String 2: T2≈5.62N
- Tension in String 3: T3≈2.81N
- For Block 1 (mass = 1 kg):
- Weight (downward force) = W1=m1⋅g=1⋅10=10N
- Tension in the strings acting upward = T1=4T (from the video)
- For Block 2 (mass = 2 kg):
- Weight (downward force) = W2=m2⋅g=2⋅10=20N
- Tension in the strings acting upward = T2=T
- For Block 1 (upward direction is positive):
4T−10=1⋅a(Equation 1)
- For Block 2 (downward direction is positive):
20−T=2⋅(7a)(Equation 2)
- From Equation 1:
4T−10=a⇒a=4T−10(1)
- From Equation 2:
20−T=14a⇒T=20−14a(2)
- Substitute a=4T−10 into T=20−14a:
T=20−14(4T−10)
T=20−56T+140
57T=160⇒T=16057≈2.81N
- Substitute T back into Equation (1):
a=4T−10=4⋅16057−10
a=64057−10=64057−57057=7057≈1.23m/s2
- Tension in String 1:
T1=4T=4⋅16057≈11.24N
- Tension in String 2:
T2=2T=2⋅16057≈5.62N
- Tension in String 3:
T3=T≈2.81N
- Acceleration of Block 1: a≈1.23m/s2 (upward)
- Tension in String 1: T1≈11.24N
- Tension in String 2: T2≈5.62N
- Tension in String 3: T3≈2.81N
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Solved Examples15videos
LAWS OF MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Miscellaneous Examples9videos
LAWS OF MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE15videos
KINEMATICS 1
- BOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Subjective18videos
LAWS OF THERMODYNAMICS
Similar Questions

Find out the acceleration of the blocks and tensions in the strings.View SolutionIn the adjacent figure, masses of A,B and C are 1kg,3kg and 2kg respectively. Find
(a) the acceleration of the system and
(b) tension in the strings.
Neglect friction.(g=10m/s2)
 View Solution
View SolutionTwo masses 2 kg and 4 kg are connected at the two ends of light inextensible string passing over a frictionless pulley. If the masses are released, then find the acceleration of the masses and the tension in the string.
View SolutionIn the adjacent figure, mass of A, B and C are 1 kg , 3 kg and 2 kg, respectively. Find

(a) the acceleration of the system, and
(b) tensions in the string .
Neglect friction. (g=10ms−2)View SolutionIn the adjacent figure, mass of A, B and C are 1 kg , 3 kg and 2 kg, respectively. Find

(a) the acceleration of the system, and
(b) tensions in the string .
Neglect friction. (g=10ms−2)View SolutionIn the adjacent figure, mass of A, B and C are 1 kg , 3 kg and 2 kg, respectively. Find

(a) the acceleration of the system, and
(b) tensions in the string .
Neglect friction. (g=10ms−2)View SolutionTwo masses 2 kg and 4 kg are connected at two ends of light inextensible string passing over a frictionless pulley . If the masses are released , then find the accelaration of the masses and the tension in the string .
View SolutionIn Fig if f1,f2 and T are the friction forces on 2kg block 3kg block and tension in the string respectively the find their value initially before applying the forces tension in string was zero
 View Solution
View SolutionIn an atwood machine the two blocks have massess 1kg and 3kg. The pulley is massless and frictionless and string is light. The acceleration of the centre of mass (in m/s2) of this system is 0.5x. Find the value of x.
View SolutionIf coeffiecient of friction between the block of mass 2kg and table is 0.4 then out acceleration of the system and tension in the string. (g=10m/s2)
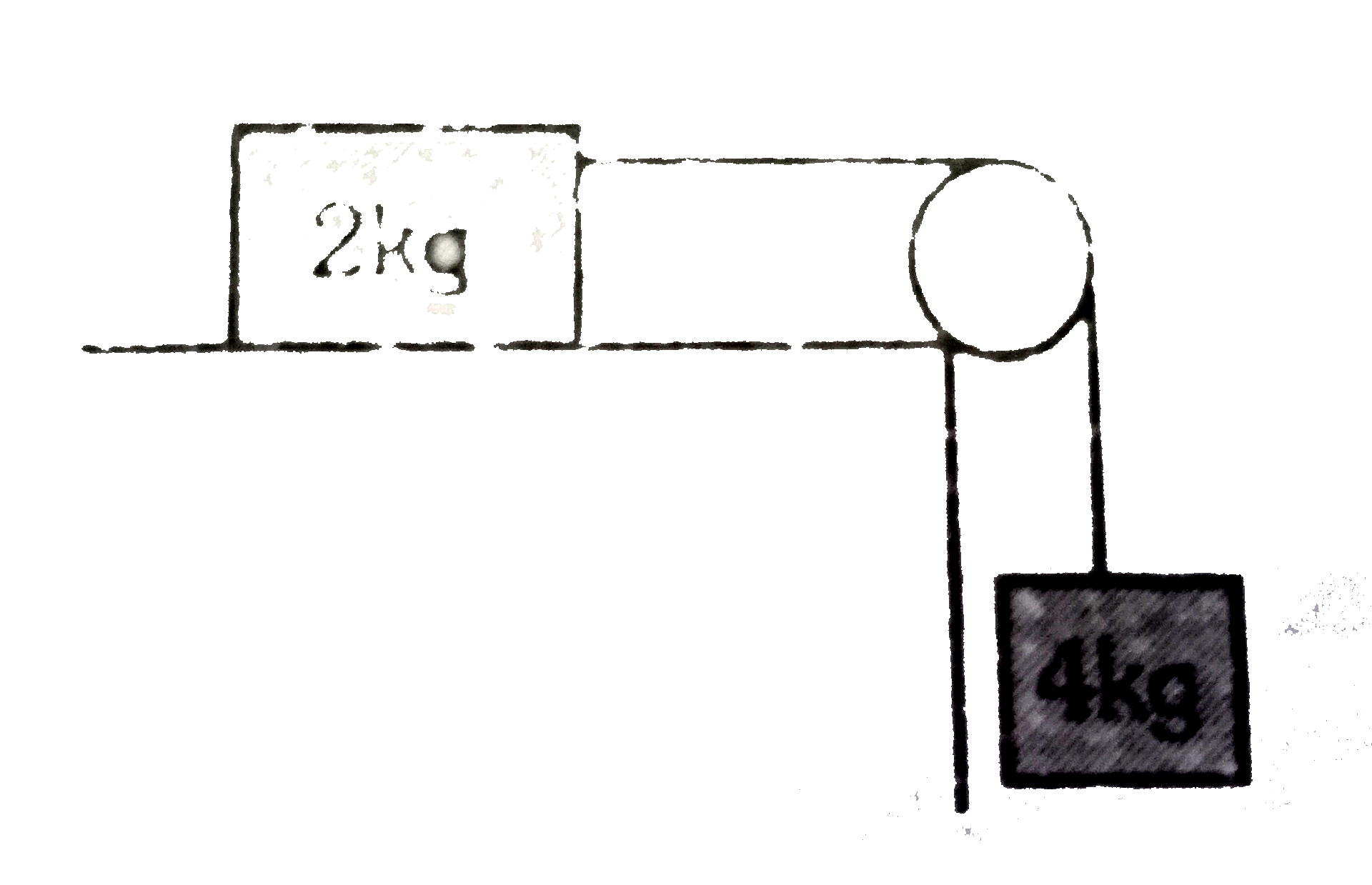 View Solution
View Solution
