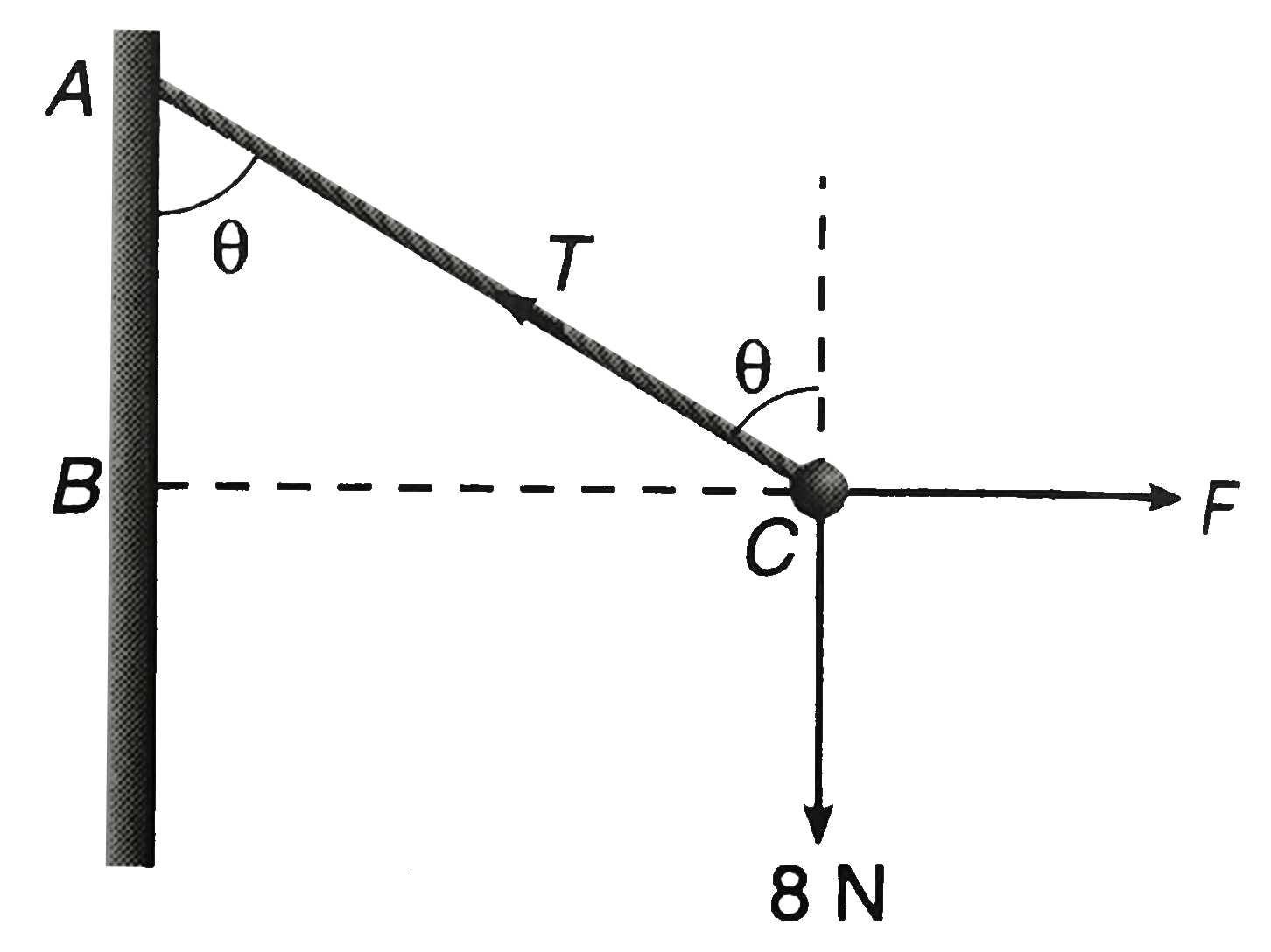
One end of a string $0.5 m$ long is fixed to a point $A$ and the other end is fastened to a small object of weight $8 N$ . The object is pulled aside by a horizontal force F, until it is $0.3 m$ from the vertical through $A$ .Find the magnitudes of the tension $T$ in the string and force $F$ .

Video Solution

Text Solution

Verified by Experts

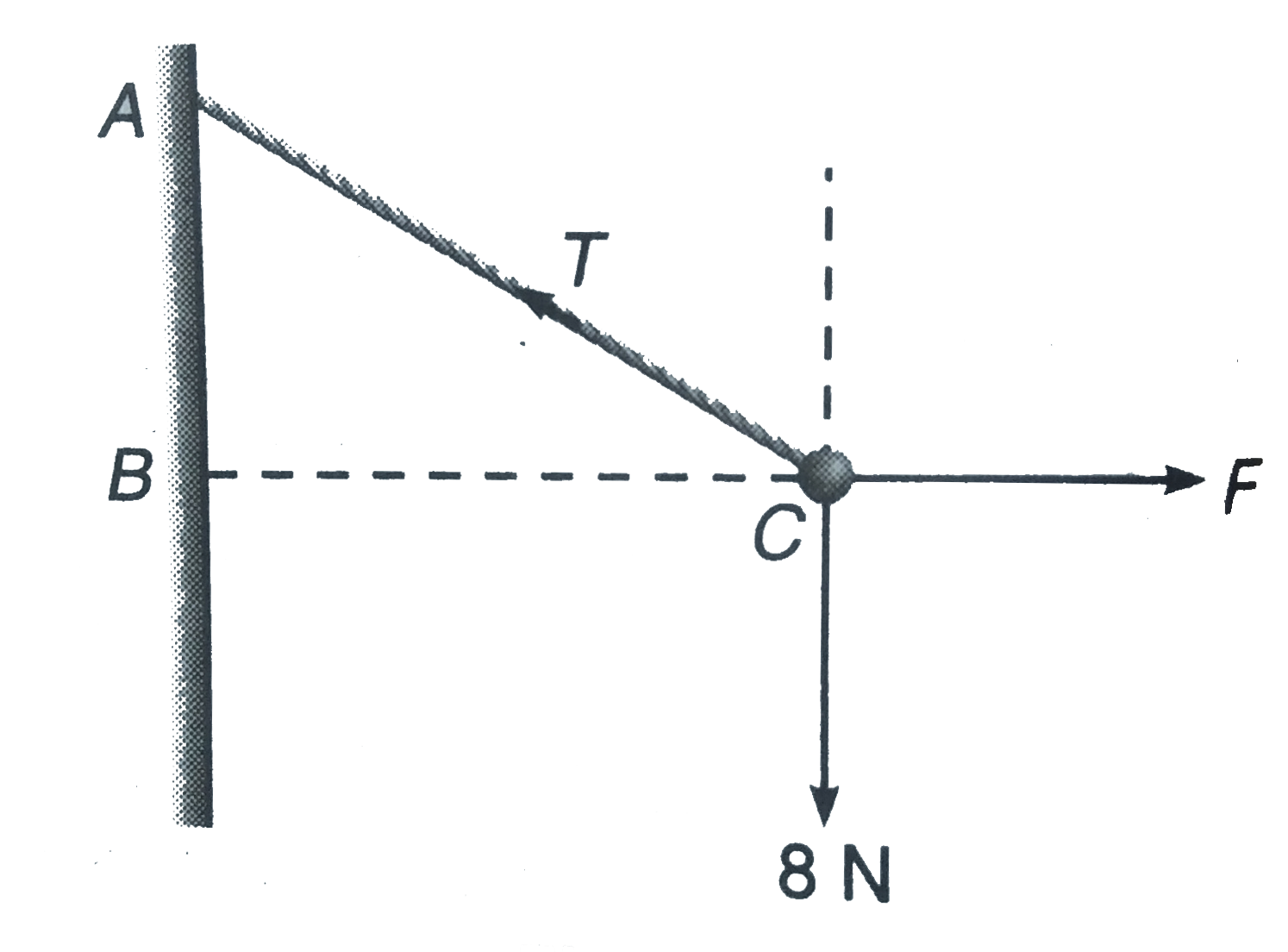
$A C = 0.5 m, B C = 0.3 m$
:. $A B = 0.4 m$
and it $∠ B A C = θ .$
Then $cos θ = \frac{A B}{A C} = \frac{0.4}{0.5} = \frac{4}{5}$
and $sin θ = \frac{B C}{A C} = \frac{0.3}{0.5} = \frac{3}{5}$
Here , the object is in equilibrium under three concurrent forces. So we can apply Lami's theorem.
or $\frac{F}{sin (180^{\circ} - θ)} = \frac{8}{sin (90^{\circ} + θ)} = \frac{T}{{sin 90}^{\circ}}$
or $\frac{F}{sin θ} = \frac{8}{cos θ} = T$
and $F = \frac{8 sin θ}{cos θ} = \frac{(8) (3 / 5)}{(4 / 5)} = 6 N$

Updated on:21/07/2023

One end of string of length $l$ is connected to a particle on mass $m$ and the other end is connected to a small peg on a smooth horizontal table. If the particle moves in circle with speed $v$ the net force on the particle (directed toward centre) will be ( $T$ reprents the tension in the string):
AT
B $T - \frac{{(m v)}^{2}}{l}$
C $T + \frac{m v^{2}}{l}$
D0