An elevator without a ceiling is ascending up with an acceleration of 5ms−2. A boy on the elevator shoots a ball in vertical upward direction from a height of 2 m above the floor of elevator. At this instant the elevator is moving up with a velocity of 10ms−1 and floor of the elevator is at a height of 50 m from the ground. The initial speed of the ball is 15ms−1 with respect to the elevator. Consider the duration for which the ball strikes the floor of elevator in answering following questions. (g=10ms−2)
3. Displacement of ball with respect to ground during its night would be
16.25 m
8.76 m
20.24 m
30.56 m
The correct Answer is:D
To solve the problem step by step, we need to calculate the displacement of the ball with respect to the ground during its flight.
Step 1: Understand the Initial Conditions
- The elevator is moving upwards with an acceleration of a=5m/s2.
- The initial velocity of the elevator ue=10m/s.
- The height of the floor of the elevator from the ground he=50m.
- The height from which the ball is shot above the floor of the elevator hb=2m.
- The initial speed of the ball with respect to the elevator ub=15m/s.
- The acceleration due to gravity g=10m/s2.
Step 2: Calculate the Initial Velocity of the Ball with Respect to the Ground
The initial velocity of the ball with respect to the ground u is the sum of the initial velocity of the elevator and the initial velocity of the ball with respect to the elevator:
u=ue+ub=10m/s+15m/s=25m/s
Step 3: Determine the Effective Acceleration Acting on the Ball
Since the elevator is accelerating upwards, the effective acceleration acting on the ball when it is shot upwards will be:
a=−g−ae=−10m/s2−5m/s2=−15m/s2
(Note: The negative sign indicates that the acceleration is acting downwards).
Step 4: Calculate the Time of Flight
To find the time of flight t until the ball strikes the floor of the elevator, we can use the kinematic equation:
s=ut+12at2
where s is the displacement of the ball with respect to the elevator. Since the ball is shot from a height of 2 m above the floor of the elevator and will fall back to that floor, we can set s=−2m (the ball moves downwards).
Substituting the known values:
−2=25t−12(15)t2
This simplifies to:
−2=25t−7.5t2
Rearranging gives us:
7.5t2−25t−2=0
Step 5: Solve the Quadratic Equation
Using the quadratic formula t=−b±√b2−4ac2a where a=7.5,b=−25,c=−2:
t=25±√(−25)2−4⋅7.5⋅(−2)2⋅7.5
Calculating the discriminant:
625+60=685
Thus,
t=25±√68515
Calculating the value gives approximately t≈2.13s (taking the positive root).
Step 6: Calculate the Displacement of the Ball with Respect to the Ground
Now, we can find the displacement of the ball with respect to the ground during its flight:
sg=ut+12(−g−ae)t2
Substituting the values:
sg=25⋅2.13+12(−15)(2.13)2
Calculating:
sg=25⋅2.13−7.5⋅(4.5369)≈53.25−34.02=19.23m
Step 7: Total Displacement from the Ground
Finally, we need to add the height of the elevator floor from the ground:
Total Displacement=he+sg=50+19.23=69.23m
Final Answer
The displacement of the ball with respect to the ground during its flight would be approximately 69.23m.
- The elevator is moving upwards with an acceleration of a=5m/s2.
- The initial velocity of the elevator ue=10m/s.
- The height of the floor of the elevator from the ground he=50m.
- The height from which the ball is shot above the floor of the elevator hb=2m.
- The initial speed of the ball with respect to the elevator ub=15m/s.
- The acceleration due to gravity g=10m/s2.
The initial velocity of the ball with respect to the ground u is the sum of the initial velocity of the elevator and the initial velocity of the ball with respect to the elevator:
u=ue+ub=10m/s+15m/s=25m/s
Since the elevator is accelerating upwards, the effective acceleration acting on the ball when it is shot upwards will be:
a=−g−ae=−10m/s2−5m/s2=−15m/s2
(Note: The negative sign indicates that the acceleration is acting downwards).
To find the time of flight t until the ball strikes the floor of the elevator, we can use the kinematic equation:
s=ut+12at2
where s is the displacement of the ball with respect to the elevator. Since the ball is shot from a height of 2 m above the floor of the elevator and will fall back to that floor, we can set s=−2m (the ball moves downwards).
−2=25t−12(15)t2
This simplifies to:
−2=25t−7.5t2
Rearranging gives us:
7.5t2−25t−2=0
Using the quadratic formula t=−b±√b2−4ac2a where a=7.5,b=−25,c=−2:
t=25±√(−25)2−4⋅7.5⋅(−2)2⋅7.5
Calculating the discriminant:
625+60=685
Thus,
t=25±√68515
Calculating the value gives approximately t≈2.13s (taking the positive root).
Now, we can find the displacement of the ball with respect to the ground during its flight:
sg=ut+12(−g−ae)t2
Substituting the values:
sg=25⋅2.13+12(−15)(2.13)2
Calculating:
sg=25⋅2.13−7.5⋅(4.5369)≈53.25−34.02=19.23m
Finally, we need to add the height of the elevator floor from the ground:
Total Displacement=he+sg=50+19.23=69.23m
The displacement of the ball with respect to the ground during its flight would be approximately 69.23m.
Topper's Solved these Questions
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - Subjective Questions
24 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - SCQ_TYPE
39 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - More Than One Correct
6 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises
45 Videos
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
Similar Questions
An elevator without a ceiling is ascending up with an acceleration of 5ms−2. A boy on the elevator shoots a ball in vertical upward direction from a height of 2 m above the floor of elevator. At this instant the elevator is moving up with a velocity of 10ms−1 and floor of the elevator is at a height of 50 m from the ground. The initial speed of the ball is 15ms−1 with respect to the elevator. Consider the duration for which the ball strikes the floor of elevator in answering following questions. (g=10ms−2)
1. The time in which the ball strikes the floor of elevator is given by
View SolutionAn elevator without a ceiling is ascending up with an acceleration of 5ms−2. A boy on the elevator shoots a ball in vertical upward direction from a height of 2 m above the floor of elevator. At this instant the elevator is moving up with a velocity of 10ms−1 and floor of the elevator is at a height of 50 m from the ground. The initial speed of the ball is 15ms−1 with respect to the elevator. Consider the duration for which the ball strikes the floor of elevator in answering following questions. (g=10ms−2)
2. The maximum height reached by ball, as measured from the ground would be
View SolutionAn elevator without a ceiling is ascending up with an acceleration of 5ms−2. A boy on the elevator shoots a ball in vertical upward direction from a height of 2 m above the floor of elevator. At this instant the elevator is moving up with a velocity of 10ms−1 and floor of the elevator is at a height of 50 m from the ground. The initial speed of the ball is 15ms−1 with respect to the elevator. Consider the duration for which the ball strikes the floor of elevator in answering following questions. (g=10ms−2)
4. The maximum separation between the floor of elevator and the ball during its flight would be
View SolutionAn elevator without a ceiling is ascending with a constant speed of 10 m//s. A boy on the elevator shoots a ball directly upward, from a height of 2.0 m above the elevator floor. At this time the elevator floor is 28 m above the ground. The initial speed of the ball with respect to the elevator is 20 m//s. (Take g=9.8m/s2)
(a) What maximum height above the ground does the ball reach?
(b) How long does the ball take to return to the elevator floor?
View Solution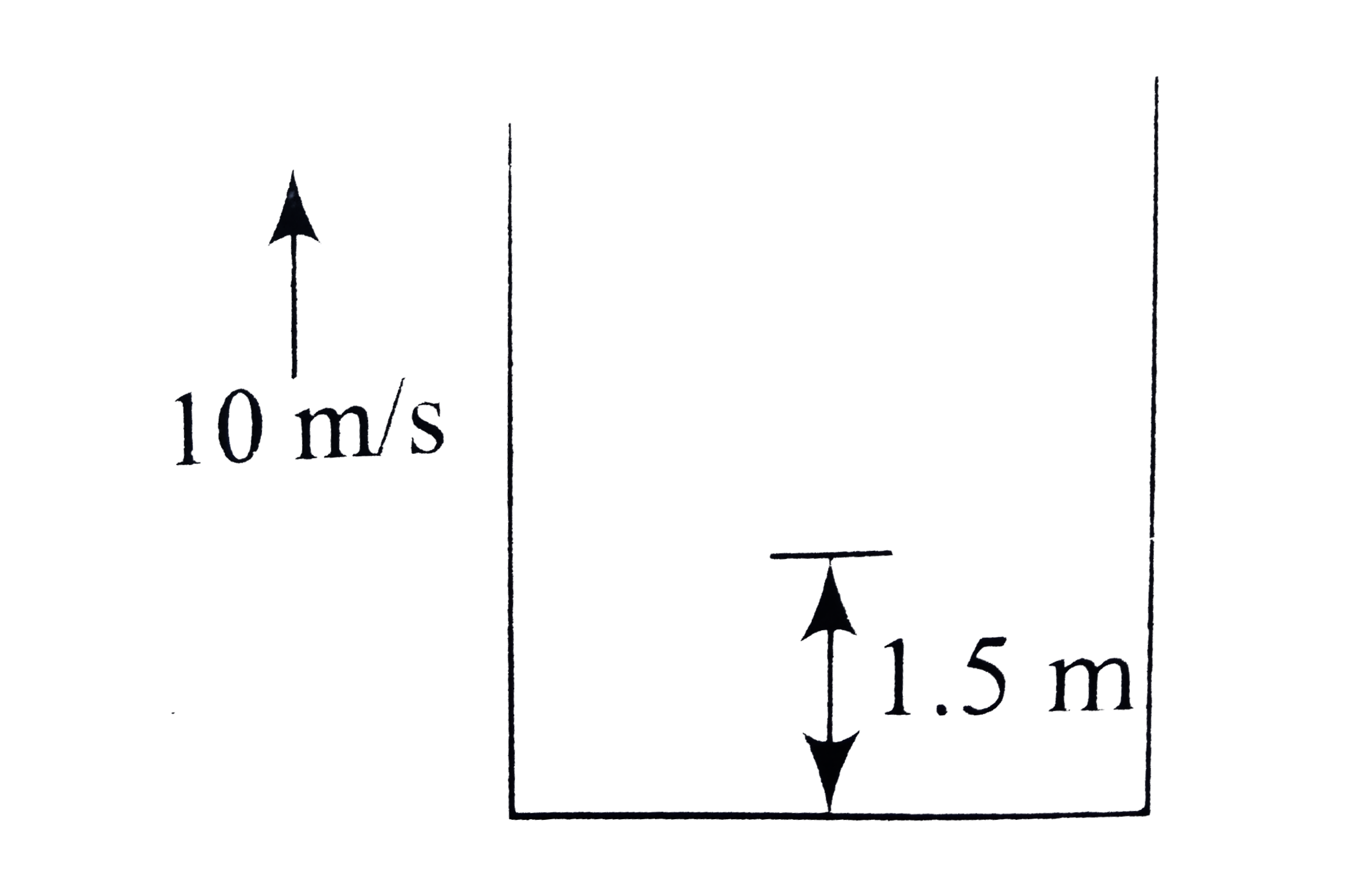
A boy in the elevator shoots a bullet in a vertical upward direction from a height of 1.5 m above the floor of the elevator. There is no roof in the elevator. The floor of the elevator is at 50 m from ground at the instant when velocity of the elevator is 10 m/s in upward direction. The bullet strikes the floor of the elevator in 2 seconds. The initial speed of the bullet is 15 m/s relative to the elevator.
Q. Find the displacement of the bullet relative to ground during its flight:
View Solution
A boy in the elevator shoots a bullet in a vertical upward direction from a height of 1.5 m above the floor of the elevator. There is no roof in the elevator. The floor of the elevator is at 50 m from ground at the instant when velocity of the elevator is 10 m/s in upward direction. The bullet strikes the floor of the elevator in 2 seconds. The initial speed of the bullet is 15 m/s relative to the elevator.
Q. Find the acceleration of the elevator in upward direction, (mss2):
View Solution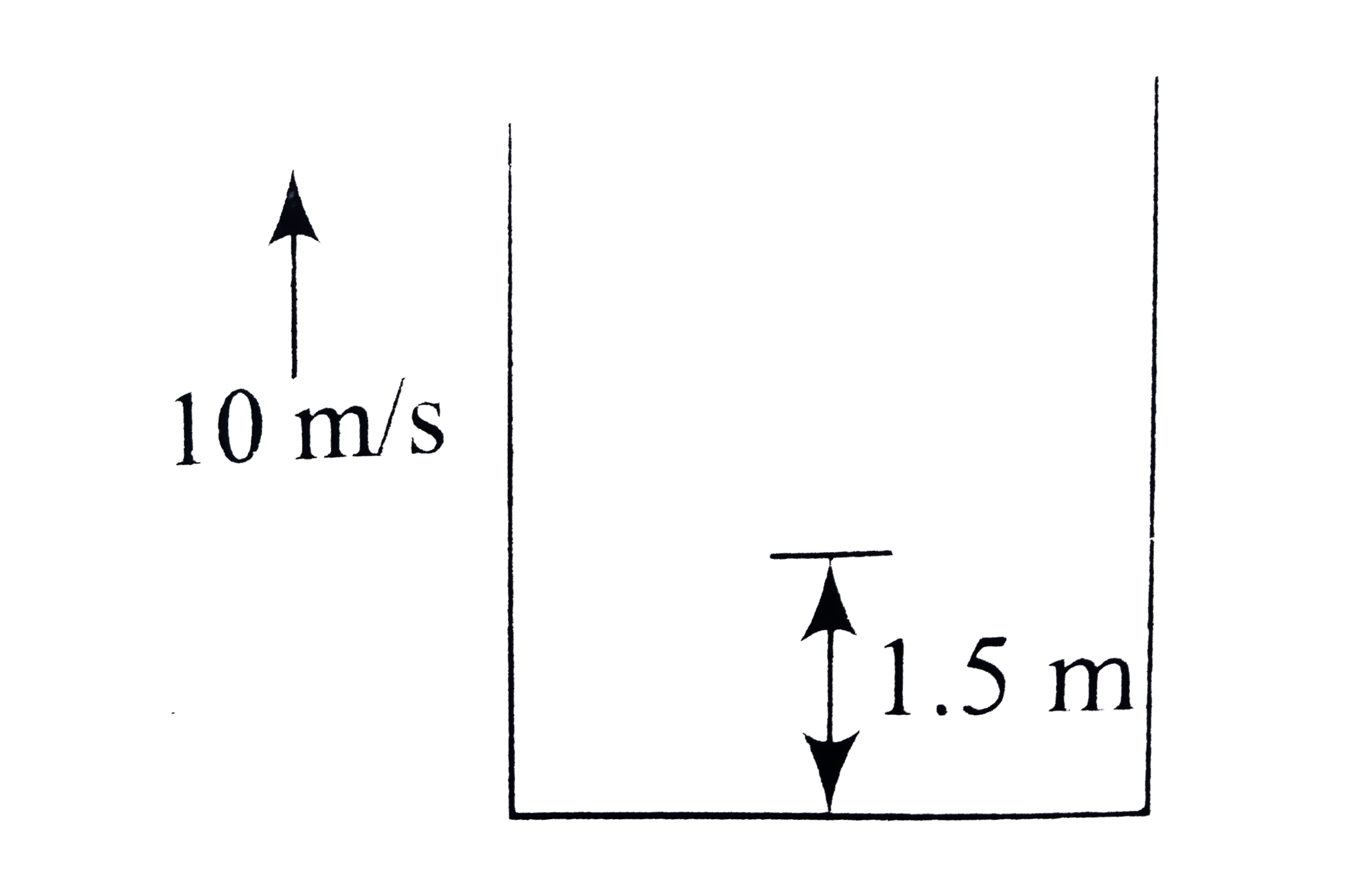
A boy in the elevator shoots a bullet in a vertical upward direction from a height of 1.5 m above the floor of the elevator. There is no roof in the elevator. The floor of the elevator is at 50 m from ground at the instant when velocity of the elevator is 10 m/s in upward direction. The bullet strikes the floor of the elevator in 2 seconds. The initial speed of the bullet is 15 m/s relative to the elevator.
Q. Find the maximum height reached by the bullet relative to the ground :
View SolutionAn elevator whose floor-to-ceiling destance is 2.50m starts ascending with a constant acceleration of 1.25ms−2 On second after the start, a bolt begins falling from the elevator. Calculate the free fall time of the bolt
View SolutionSuppose the ceiling in the previous problem is that the elevator which is going up with an acceleration of 2.0ms2. Find the elongations.
View SolutionStarting from rest, A lift moves up with an acceleration of 2ms−2. In this lift , a ball is dropped from a height of 1.5m (with respect to floor of lift). The time taken by the ball to reach the floor of the lift is (g=10ms−2)
View Solution
