The contripetal force F acting on a particle moving uniformly in a circle may depend upon mass (m), velocity (v) and redio ( r) of the circle . Derive the formula for F using the method of dimensions.
To derive the formula for centripetal force F using the method of dimensions, we will follow these steps:
Step 1: Identify the variables
The centripetal force F may depend on mass m, velocity v, and radius r. We can express this relationship as:
F=k⋅ma⋅vb⋅rc
where k is a dimensionless constant, and a,b,c are the powers to be determined.
Step 2: Write the dimensions of each variable
- The dimension of force F is:
(F)=(M1L1T−2)
- The dimension of mass m is:
(m)=(M1)
- The dimension of velocity v is:
(v)=(L1T−1)
- The dimension of radius r is:
(r)=(L1)
Step 3: Substitute the dimensions into the equation
Now, substituting the dimensions into our equation:
(M1L1T−2)=(M1)a⋅(L1)b⋅(L1)c
This simplifies to:
(M1L1T−2)=(MaLb+cT−b)
Step 4: Equate the dimensions
Now we equate the dimensions on both sides:
1. For mass M:
a=1
2. For length L:
b+c=1
3. For time T:
−b=−2⟹b=2
Step 5: Solve for c
Using b=2 in the equation b+c=1:
2+c=1⟹c=1−2=−1
Step 6: Substitute the values back into the equation
Now substituting the values of a,b,c back into the equation for F:
F=k⋅m1⋅v2⋅r−1
This can be rewritten as:
F=k⋅mv2r
Step 7: Finalize the formula
Assuming k=1 for simplicity, we arrive at the formula for centripetal force:
F=mv2r
Summary
Thus, the formula for centripetal force F acting on a particle moving uniformly in a circle is:
F=mv2r
The centripetal force F may depend on mass m, velocity v, and radius r. We can express this relationship as:
F=k⋅ma⋅vb⋅rc
where k is a dimensionless constant, and a,b,c are the powers to be determined.
- The dimension of force F is:
(F)=(M1L1T−2)
- The dimension of mass m is:
(m)=(M1)
- The dimension of velocity v is:
(v)=(L1T−1)
- The dimension of radius r is:
(r)=(L1)
Now, substituting the dimensions into our equation:
(M1L1T−2)=(M1)a⋅(L1)b⋅(L1)c
This simplifies to:
(M1L1T−2)=(MaLb+cT−b)
Now we equate the dimensions on both sides:
1. For mass M:
a=1
2. For length L:
b+c=1
3. For time T:
−b=−2⟹b=2
Using b=2 in the equation b+c=1:
2+c=1⟹c=1−2=−1
Now substituting the values of a,b,c back into the equation for F:
F=k⋅m1⋅v2⋅r−1
This can be rewritten as:
F=k⋅mv2r
Assuming k=1 for simplicity, we arrive at the formula for centripetal force:
F=mv2r
Thus, the formula for centripetal force F acting on a particle moving uniformly in a circle is:
F=mv2r
Topper's Solved these Questions
- UNIT AND DIMENSIONSBOOK - DC PANDEY ENGLISHCHAPTER - UNIT AND DIMENSIONSEXERCISE - Single Correct
20 Videos
- UNIT AND DIMENSIONSBOOK - DC PANDEY ENGLISHCHAPTER - UNIT AND DIMENSIONSEXERCISE - More Than One Correct
5 Videos
- THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESBOOK - DC PANDEY ENGLISHCHAPTER - THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESEXERCISE - Level 2 Subjective
9 Videos
- UNITS, DIMENSIONS & ERROR ANALYSIS BOOK - DC PANDEY ENGLISHCHAPTER - UNITS, DIMENSIONS & ERROR ANALYSIS EXERCISE - Medical entrances gallery
32 Videos
Similar Questions
The centripetal force F acting on a particle moving uniformly in a circle may depend upon mass (m), velocity (v) and radius ( r) of the circle . Derive the formula for F using the method of dimensions.
View SolutionThe kinetic energy K of a particle moving along a circle of radius R depends upon the distance s as K=as2. The force acting on the particle is
View SolutionCentripetal acceleration of a particle of mass m moving in a circle of radius r is 4/r2. What is the angular momentum of the particle ?
View SolutionA body of mass m is moving in a circle of radius angular velocity ω. Find the expression for centripetal force acting on it by the method of dimensions
View SolutionThe buoyant force F acting on a body depends on the density of medium ρ, volume of body immerese V and acceleration due to gravity g. Establish the relation using method of dimensions.
View SolutionA force F1 acts on a particle so as to accelerate it from rest to a velocity v. The force F1 is then replaced by F2 which decelerates it to rest
View SolutionPower of the only force acting on a particle of mass m=1 kg moving in straight line depends on its velocity as P=v2 where v is in m/s and P is in watt. If initial velocity of the particle is 1m/s, then the displacement of the particle in ln2 second will be :
View SolutionThe force F acting on a particle is moving in a straight line as shown in figure. What is the work done by the force on the particle in the 4 m of the trajectory?
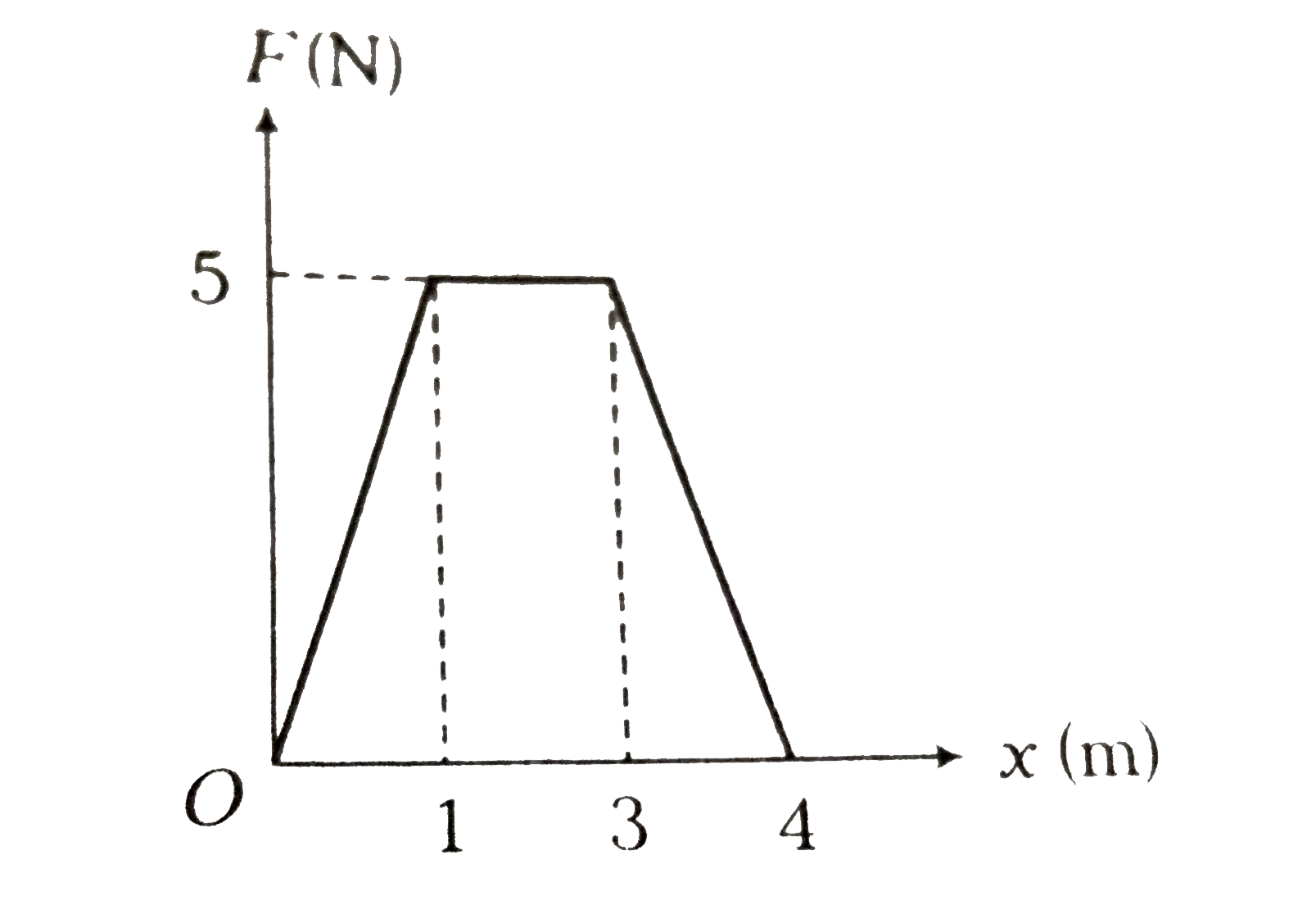
View SolutionA force F1 acts on a particle so as to accelerate it from rest to a velocity v. The force F1 is then replaced by F2 which decelerates it to rest.
View SolutionIf force (F), velocity (V) and time (T) are taken as fundamental units, then the dimensions of mass are
View Solution
