A function f is defined by f(x)=|x|m|x−1|n∀x∈R . The local maximum value of the function is , (m,n∈N)Solution in Telugu
1
mnnm
mmnn(m+n)m+n
(mn)mn(m+n)m+n
The correct Answer is:C
Step by step video, text & image solution for A function f is defined by f(x)=|x|^(m)|x-1|^(n)AAx inR . The local maximum value of the function is , (m,ninN) by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MAXIMA AND MINIMA BOOK - AAKASH SERIESCHAPTER - MAXIMA AND MINIMA EXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - II (LECTURE SHEET )(ADVANCED)) (MORE THAN ONE CORRECT ANSWER TYPE QUESTIONS)
10 Videos
- MAXIMA AND MINIMA BOOK - AAKASH SERIESCHAPTER - MAXIMA AND MINIMA EXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - II (LECTURE SHEET )(ADVANCED)) (MATRIX MATCHING TYPE QUESTIONS)
2 Videos
- MAXIMA AND MINIMA BOOK - AAKASH SERIESCHAPTER - MAXIMA AND MINIMA EXERCISE - PRACTICE SHEET (EXERCISE -II) (LEVEL -II)(INTEGER TYPE QUESTIONS)
4 Videos
- MAXIMA & MINIMABOOK - AAKASH SERIESCHAPTER - MAXIMA & MINIMAEXERCISE - EXERCISE-III
35 Videos
- MEAN VALUE THEOREMSBOOK - AAKASH SERIESCHAPTER - MEAN VALUE THEOREMSEXERCISE - PRACTICE SHEET (EXERCISE-I (LEVEL-II (MORE THAN ONE CORRECT ANSWER TYPE QUESTIONS ) )
2 Videos
Similar Questions
Let f(x)=(x−1)4(x−2)n, n in N.. Then f(x) has
View SolutionThe function f(x)=√(ax3+bx2+cx+d) has its nonzero local minimum an d maximum values at x=-2 andx=2 , repectively . If a is a root of x2−x−x6=0 , then match the following
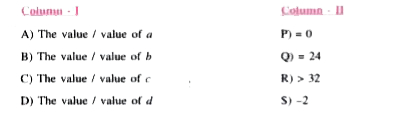
View SolutionA right triangle is drawn in a semicircle of radius 12 with one of its legs along the diameter . If the maximum area of the triangle is M , then the value of 32√3Mc is _______
View SolutionThe maximum slope of the curve y=−x3+3x2+9x−27 is
View SolutionGiven f(x) = 4- ((1)/(2) - x)^(2//3) , g(x) = {:{((tan[x])/(x),","x cancel(=)0),(1,","x=0):}" "h(x)={x}, k (x) = 5^(log_(2)(x+3))
Then in [0,1], Lagrange's mean value theorem is not applicable to (where [.] and {.} represents the greatest integer functions and fractions part functions, respectively )
View SolutionLetf:R→R be a real function. The function f is double differentiable. If there exists n∈N and p∈R such that limx→∞xnf(x)=p and there exists limx→∞xn+1f(x),then
limx→∞xn+1f'(x) is equal to
View SolutionLetf:R→R be a real function. The function f is double differentiable. If there exists n∈N and p∈R such that limx→∞xnf(x)=p and there exists limx→∞xn+1f(x),then
limx→∞xn+2f''(x) is equal to
View SolutionFind the minimum value of the function
f(x)=(1+sinx)(1+cosx),∀x∈R.
View Solutionदिखाइए कि फलन f(x)=c=sinx,∀x∈R के लिये वृद्धिमान फलन है.
View Solutionनिम्नलिखित फलन f और g के लिए f+g का मान ज्ञात कीजिए -
f(x)=x4,∀x∈R और g(x)=x−1,∀x∈R.
View Solutionमान लीजिए कि फलन R→R,f(x)=cosx,∀x∈R, द्वारा परिभाषित है । सिद्ध कीजिए कि f न तो एकैकी है और न आच्छादक (आच्छदि) है ।
View SolutionIf M and m are the maximum and minimum values respectively of the function f(x)=x+1x , then the value of M - m is-
View SolutionFind the minimum value of the function
f(x)=(1+sinx)(1+cosx),∀x∈R.
View Solutionसिद्ध कीजिए कि f(x)=xx2+1,∀x∈R, द्वारा परिभाषित फलन f:R→R न तो एकेकी है और न आच्छादि है।
View SolutionLet f(x)=(x−1)m(x−2)n,x∈R then each critical point of f(x) is either local maximum or local minimum where
View Solution
