The fuel charges for running a train are proportional to the square of the speed generated in km/h, and the cost is Rs . 48 at 16 km/h . It the fixed charges amount to Rs. 300/h , the most economical speed is Solution in Telugu
60km/h
40km/h
48km/h
36km/h
The correct Answer is:B
Step by step video, text & image solution for The fuel charges for running a train are proportional to the square of the speed generated in km/h, and the cost is Rs . 48 at 16 km/h . It the fixed charges amount to Rs. 300/h , the most economical speed is by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MAXIMA AND MINIMA Book:AAKASH SERIESChapter:MAXIMA AND MINIMA Exercise:ADDITIONAL PRACTICE EXERCISE (LEVEL - II (LECTURE SHEET )(ADVANCED)) (MORE THAN ONE CORRECT ANSWER TYPE QUESTIONS)
Explore 10 Videos
- MAXIMA AND MINIMA Book:AAKASH SERIESChapter:MAXIMA AND MINIMA Exercise:ADDITIONAL PRACTICE EXERCISE (LEVEL - II (LECTURE SHEET )(ADVANCED)) (MATRIX MATCHING TYPE QUESTIONS)
Explore 2 Videos
- MAXIMA AND MINIMA Book:AAKASH SERIESChapter:MAXIMA AND MINIMA Exercise:PRACTICE SHEET (EXERCISE -II) (LEVEL -II)(INTEGER TYPE QUESTIONS)
Explore 4 Videos
- MAXIMA & MINIMABook:AAKASH SERIESChapter:MAXIMA & MINIMAExercise:EXERCISE-III
Explore 35 Videos
- MEAN VALUE THEOREMSBook:AAKASH SERIESChapter:MEAN VALUE THEOREMSExercise:PRACTICE SHEET (EXERCISE-I (LEVEL-II (MORE THAN ONE CORRECT ANSWER TYPE QUESTIONS ) )
Explore 2 Videos
Similar Questions
Let f(x)=(x−1)4(x−2)n, n in N.. Then f(x) has
View SolutionThe function f(x)=√(ax3+bx2+cx+d) has its nonzero local minimum an d maximum values at x=-2 andx=2 , repectively . If a is a root of x2−x−x6=0 , then match the following
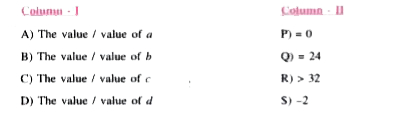
View SolutionA right triangle is drawn in a semicircle of radius 12 with one of its legs along the diameter . If the maximum area of the triangle is M , then the value of 32√3Mc is _______
View SolutionThe maximum slope of the curve y=−x3+3x2+9x−27 is
View SolutionGiven f(x) = 4- ((1)/(2) - x)^(2//3) , g(x) = {:{((tan[x])/(x),","x cancel(=)0),(1,","x=0):}" "h(x)={x}, k (x) = 5^(log_(2)(x+3))
Then in [0,1], Lagrange's mean value theorem is not applicable to (where [.] and {.} represents the greatest integer functions and fractions part functions, respectively )
View SolutionThe fuel charges for running a train are proportional to the square of the speed generated in km/h, and the cost is Rs. 48 at 16 km/h. If the fixed charges amount to Rs. 300/h, the most economical speed is (a) 60 km/h (b) 40 km/h 48 km/h (d) 36 km/h
View SolutionThe cost of running a bus from A to B, is Rs. (av + b/v), where v km/h is the average speed of the bus. When the bus travels at 30 km/h, the cost comes out to be Rs. 75 while at 40 km/h, it is Rs. 65.Then the most economical speed (in km/h) of the bus is :
View SolutionThe expenditure on fuels in running a train varies as the square of its speed measured in km/hr and it is Rs. 48 per hour at the speed of 16 km/hr. If the constant expenditure is Rs. 300 per hour find the best speed of the train economically.
View Solutionएक रेलगाड़ी को चलने में ईंधन का खर्च उसकी किमी प्रति घण्टा कि इकाइयों में नापी गति के वर्ग के अनुक्रमानुपाती है तथा 16 किमी प्रति घण्टा के वेग पर रु 48 प्रति घण्टा है। यदि स्थित व्यय रु 300 प्रति घण्टा है, तो आर्थिक दृष्टि से सबसे अच्छा वेग क्या होगा ?
View SolutionThe fuel charges for running a train are proportional to the square of the speed generated in km per hour and cost Rs 100 per hour at 20km/hr. If the fixed charge amount to Rs. 10,000 per hour, the most economical speed in km per hour is equal to K, then k/50=
View SolutionThe fuel charges for running a train are proportional to the square of the speed generated in km/h, and the cost is Rs. 48 at 16 km/h. If the fixed charges amount to Rs. 300/h, the most economical speed is (a) 60 km/h (b) 40 km/h 48 km/h (d) 36 km/h
View Solution40 किमी/घण्टा की चाल से चलती रेलगाड़ी अपने समान्तर 25 किमी/घण्टा की चाल से चलते हुए एक व्यक्ति को 48 सेकण्ड में पार करती है। गाड़ी की लम्बाई होगी
View SolutionThe fuel charges for running a train are proportional to the square of the speed generated in km/h, and the cost is Rs. 48 at 16 km/h. If the fixed charges amount to Rs. 300/h, the most economical speed is (a) 60 km/h (b) 40 km/h 48 km/h (d) 36 km/h
View SolutionThe fuel charges for running a train are proportional to the square of the speed generated in km/h, and the cost is Rs. 48 at 16 km/h. If the fixed charges amount to Rs. 300/h, the most economical speed is 60 km/h (b) 40 km/h 48 km/h (d) 36 km/h
View SolutionThe fuel charges for running a train are proportional to the square of the speed generated in km/h, and the cost is Rs. 48 at 16 km/h. If the fixed charges amount to Rs. 300/h, the most economical speed is (a) 60 km/h (b) 40 km/h 48 km/h (d) 36 km/h
View Solution

