If f(x)=xsinxandg(x)=xtanx, where 0<x≤1 , then in this intervalSolution in Telugu
both f(x) and g(x) are increasing functions
both f(x) and g(x) are decreasing functions
f(x) is an increasing function
g(x) is an increasing funtion
The correct Answer is:C
Step by step video & text solution for If f(x)=(x)/(sinx)andg(x)=(x)/(tanx), where 0ltxle1 , then in this interval by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - MAXIMA AND MINIMA EXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - II (LECTURE SHEET )(ADVANCED)) (MORE THAN ONE CORRECT ANSWER TYPE QUESTIONS)10videos
MAXIMA AND MINIMA
- BOOK - AAKASH SERIESCHAPTER - MAXIMA AND MINIMA EXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - II (LECTURE SHEET )(ADVANCED)) (MATRIX MATCHING TYPE QUESTIONS)2videos
MAXIMA AND MINIMA
- BOOK - AAKASH SERIESCHAPTER - MAXIMA AND MINIMA EXERCISE - PRACTICE SHEET (EXERCISE -II) (LEVEL -II)(INTEGER TYPE QUESTIONS)4videos
MAXIMA AND MINIMA
- BOOK - AAKASH SERIESCHAPTER - MAXIMA & MINIMAEXERCISE - EXERCISE-III35videos
MAXIMA & MINIMA
- BOOK - AAKASH SERIESCHAPTER - MEAN VALUE THEOREMSEXERCISE - PRACTICE SHEET (EXERCISE-I (LEVEL-II (MORE THAN ONE CORRECT ANSWER TYPE QUESTIONS ) )2videos
MEAN VALUE THEOREMS
Similar Questions
Let f(x)=(x−1)4(x−2)n, n in N.. Then f(x) has
View SolutionThe function f(x)=√(ax3+bx2+cx+d) has its nonzero local minimum an d maximum values at x=-2 andx=2 , repectively . If a is a root of x2−x−x6=0 , then match the following
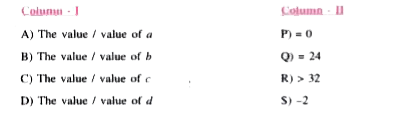 07:25View Solution
07:25View SolutionA right triangle is drawn in a semicircle of radius 12 with one of its legs along the diameter . If the maximum area of the triangle is M , then the value of 32√3Mc is _______
03:42View SolutionThe maximum slope of the curve y=−x3+3x2+9x−27 is
05:28View SolutionGiven f(x) = 4- ((1)/(2) - x)^(2//3) , g(x) = {:{((tan[x])/(x),","x cancel(=)0),(1,","x=0):}" "h(x)={x}, k (x) = 5^(log_(2)(x+3))
Then in [0,1], Lagrange's mean value theorem is not applicable to (where [.] and {.} represents the greatest integer functions and fractions part functions, respectively )01:38View SolutionIf f(x)=sinx+|sinx|andg(x)=f(x−π)+f(x+2π), then value of 5πf−2πg(x)dx is
04:08View Solutionf(x)=xsinxandg(x)=xtanx , where 0<x≤1 then in the interval
05:26View SolutionFor x∈R,f(x)=|log2−sinx|andg(x)=f(f(x)), then
06:04View Solutionयदि f(x)=xsinx और g(x)=xtanx, जहाँ 0<x≤1, तब इस अंतराल में
05:28View SolutionLet f(x)=x2andg(x)=sinx for all x∈R. Then the set of all x satisfying :
(fogogof)(x)=(gogof)(x), where (fog)(x)=f(g(x)), is :06:15View SolutionThe function f(x)=sinxx is decreasing in the interval
04:53View SolutionProve that the function are increasing for the given intervals: f(x)=sinx+tanx−2x,x∈(0,π2)
02:22View SolutionIf f(x)=(x(sinx+tanx))/([(x+pi)/(pi)]1/2) Where [] denotes the greatest integer function
02:04View SolutionIf f(x)=(x)/(sinx) And g(x)=(x)/(tanx) , Where 0ltxle1 , Then in this interval
05:45View SolutionIf f(x)=(x)/(sinx) And g(x)=(x)/(tanx) , Where 0ltxle1 , Then in this interval
02:31View Solution
