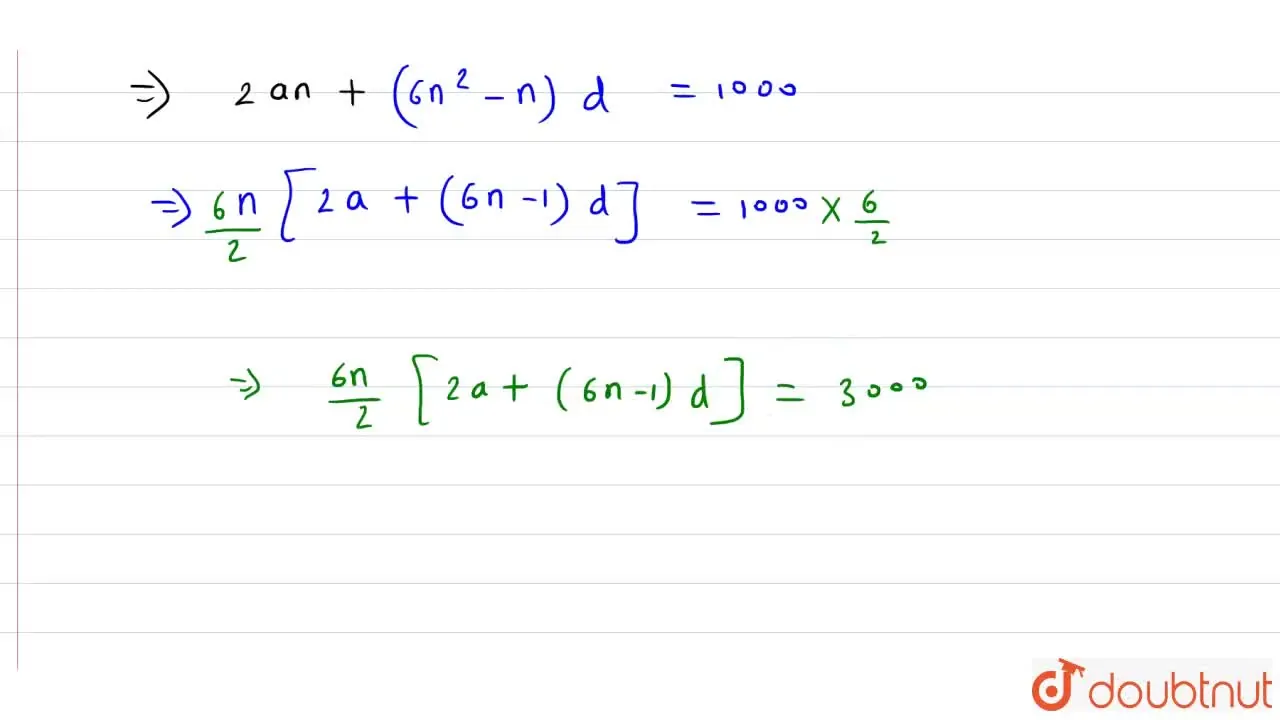If S1is the sum of first 2n terms and S2 is the sum of first 4n term and S2−S1 is equal to 1000 then S3 sum of first 6n terms of same A.P
3000
5000
7000
9000
The correct Answer is:A
Step by step video, text & image solution for If S_1is the sum of first 2n terms and S_2 is the sum of first 4n term and S_2-S_1 is equal to 1000 then S_3 sum of first 6n terms of same A.P by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
If the sum of first n terms of a G.P. is S and the sum of its first 2n terms is 5S, then show that the sum of its first 3n terms is 21S.
View SolutionIf the sum of first n terms of a G.P. is s and the sum of its first 2n terms is 5S, then show that the sum of its first 3n terms is 21S .
View SolutionIf the sum of the first 2n terms of the A.P.2,5,8,…, is equal to the sum of the first n terms of the A.P.57,59,61,…, then n equals
View SolutionIn an A.P, the sum of first 2n terms is equal to the sum of next n terms. Then the ratio of the sum of first 3n terms to the next n terms is
View SolutionIf s is the sum to infnity of a G.P, whose first term is a, then the sum of the first n terms of the G.P. is
View SolutionLet S1 be the sum of first 2n terms of an arithmetic progression. Let S2 be the sum first 4n terms of the same arithmeti progression. If (S2−S1) is 1000, then the sum of the first 6n term of the arithmetic progression is equal to :
View SolutionIf Sn the sum of first n terms of an AP is given by 2n2+n, then find its nth term.
View SolutionIf the sum of the first n terms of an A.P. is 4n−n2, what is the first term (that is S1) ? What is the sum of first two terms? What is the second term ? Similarly, find the 3rd, the 10th and ten nth terms.
View SolutionLet Sn denote the sum of the first n terms of an AP
S2n=3Sn Then the ratio S3nSn is equal toView SolutionIf S is the sum to infinite terms of a G.P whose first term is 'a', then the sum of the first n terms is
View Solution