Find out the ratio CpCv of polyatomic gas for 2 vibrational degree of freedom
The correct Answer is:1.25
To find the ratio CpCv for a polyatomic gas with 2 vibrational degrees of freedom, we can follow these steps:
Step 1: Identify the degrees of freedom for a polyatomic gas
For a polyatomic gas, the degrees of freedom can be categorized as:
- Translational degrees of freedom: 3 (movement in x, y, and z directions)
- Rotational degrees of freedom: 3 (rotation about three axes)
- Vibrational degrees of freedom: Given as 2 in this case
Step 2: Calculate the total degrees of freedom (F)
The total degrees of freedom F for the gas can be calculated as:
F=Translational+Rotational+Vibrational=3+3+2=8
Step 3: Use the formula for the ratio CpCv
The ratio CpCv (denoted as γ) can be calculated using the formula:
γ=CpCv=1+2F
Step 4: Substitute the value of F into the formula
Substituting F=8 into the formula gives:
γ=1+28=1+14=1+0.25=1.25
Step 5: Conclusion
Thus, the ratio CpCv for the polyatomic gas with 2 vibrational degrees of freedom is:
1.25
For a polyatomic gas, the degrees of freedom can be categorized as:
- Translational degrees of freedom: 3 (movement in x, y, and z directions)
- Rotational degrees of freedom: 3 (rotation about three axes)
- Vibrational degrees of freedom: Given as 2 in this case
The total degrees of freedom F for the gas can be calculated as:
F=Translational+Rotational+Vibrational=3+3+2=8
The ratio CpCv (denoted as γ) can be calculated using the formula:
γ=CpCv=1+2F
Substituting F=8 into the formula gives:
γ=1+28=1+14=1+0.25=1.25
Thus, the ratio CpCv for the polyatomic gas with 2 vibrational degrees of freedom is:
1.25
Topper's Solved these Questions
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - SECTION-A
80 Videos
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - SECTION-B
40 Videos
- JEE MAINBOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINEXERCISE - All Questions
473 Videos
- JEE MAIN 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2022EXERCISE - Question
492 Videos
Similar Questions
For a polyatomic ideal gas, vibrational degree are 24. CpCv is
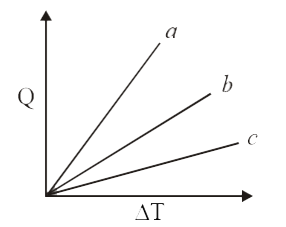
View SolutionFigure shows the variation in temperature (DT) with the amount of heat supplied (Q) in an isobaric process corresponding to a monoatomic (M), diatomic (D) and a polyatomic (P) gas. The initial state of all the gases are the same and the scales for the two axes coincide. Ignoring vibrational degrees of freedom, the lines a, b and c respectively correspond to
View Solution
Knowledge Check
A gas that has 3 degrees of freedom is
AmonoatomicBdiatomicCtriatomicDpolyatomicThe ratio of the number of moles of a monoatomic to a polyatomic gas in a mixture of the two, behaving as an diatomic gas is : (vibrational modes of freedom is to be ignored)
A2:1B1:2C2:3D3:2Assertion : Vibrational degree of freedom of a di-atomic gas molecule appears at every high temperature
Reason : Di-atomic gas has two vibrational degree of freedom in one direction.AIf both assertion and reason are true and reason is the correct explanation of assertion.BIf both assertion and reason are true but reason is the currect explanation of assertion.CIf assertion is true but reason is false.DIf both assertion and reason are false.
Find CpCv for monatomic ideal gas.
View Solution1 mole of an ideal gas undergo adiabatic process which increases temperature from 270C→370C . Gas is polyatomic has 4 vibrational mode of freedom. Find net work
View SolutionThe ratio (CpCv) for a gas is 1.29 . What is the degree of freedom of the molecules of this gas?
View SolutionMolecules of an ideal gas are known to have three translational degrees of freedom and two rotational degrees of freedom . The gas is maintained at a temperature of T. The total internal energy , U of a mole of this gas, and the value of γ(=CPCv) are given, respectively , by :
View SolutionFor an ideal diatomic gas, during any process T=KV, find out the molar heat capacity of the gas during process (neglecting vibrational degree of freedom)
View Solution
