A car accelerates from rest at a constant rate α for sometime , after which it decelerates at a constant rate β and comes to rest. If T is the total time elapsed, the maximum velocity acquired by the car is
(αβα+β)T
((α+βαβ)T
(α2+β2αβ)T
12αTβ
The correct Answer is:A
To solve the problem step by step, we will analyze the motion of the car during its acceleration and deceleration phases.
Step 1: Understand the Motion Phases
The car accelerates from rest at a constant rate α for a time t1, reaches a maximum velocity Vmax, and then decelerates at a constant rate β for a time t2 until it comes to rest.
Step 2: Apply the First Equation of Motion for Acceleration
Using the first equation of motion:
\( V = U + at \)
Where:
- \( V \) is the final velocity (which is Vmax),
- \( U \) is the initial velocity (which is 0 since the car starts from rest),
- \( a \) is the acceleration (α),
- \( t \) is the time of acceleration (t1).
Substituting the known values:
\( Vmax = 0 + α \cdot t1 \)
This simplifies to:
\( Vmax = α \cdot t1 \)
From this, we can express t1 as:
\( t1 = \frac{Vmax}{α} \)
Step 3: Apply the First Equation of Motion for Deceleration
Now, during the deceleration phase, we again use the first equation of motion:
\( V = U + at \)
Where:
- \( V \) is the final velocity (which is 0 since the car comes to rest),
- \( U \) is the initial velocity (which is Vmax),
- \( a \) is the deceleration (which is −β),
- \( t \) is the time of deceleration (t2).
Substituting the known values:
\( 0 = Vmax - β \cdot t2 \)
Rearranging gives:
\( β \cdot t2 = Vmax \)
From this, we can express t2 as:
\( t2 = \frac{Vmax}{β} \)
Step 4: Relate Total Time to Acceleration and Deceleration Times
The total time T is the sum of the acceleration time t1 and the deceleration time t2:
\( T = t1 + t2 \)
Substituting the expressions for t1 and t2:
\( T = \frac{Vmax}{α} + \frac{Vmax}{β} \)
Step 5: Factor Out Vmax
Factoring out Vmax from the equation:
\( T = Vmax \left( \frac{1}{α} + \frac{1}{β} \right) \)
This can be rewritten as:
\( T = Vmax \cdot \frac{α + β}{αβ} \)
Step 6: Solve for Vmax
Now, we can solve for Vmax:
\( Vmax = \frac{T \cdot αβ}{α + β} \)
Final Expression for Maximum Velocity
Thus, the maximum velocity acquired by the car is:
\( Vmax = \frac{αβ}{α + β} \cdot T \)
The car accelerates from rest at a constant rate α for a time t1, reaches a maximum velocity Vmax, and then decelerates at a constant rate β for a time t2 until it comes to rest.
Using the first equation of motion:
\( V = U + at \)
Where:
- \( V \) is the final velocity (which is Vmax),
- \( U \) is the initial velocity (which is 0 since the car starts from rest),
- \( a \) is the acceleration (α),
- \( t \) is the time of acceleration (t1).
\( Vmax = 0 + α \cdot t1 \)
This simplifies to:
\( Vmax = α \cdot t1 \)
From this, we can express t1 as:
\( t1 = \frac{Vmax}{α} \)
Now, during the deceleration phase, we again use the first equation of motion:
\( V = U + at \)
Where:
- \( V \) is the final velocity (which is 0 since the car comes to rest),
- \( U \) is the initial velocity (which is Vmax),
- \( a \) is the deceleration (which is −β),
- \( t \) is the time of deceleration (t2).
\( 0 = Vmax - β \cdot t2 \)
Rearranging gives:
\( β \cdot t2 = Vmax \)
From this, we can express t2 as:
\( t2 = \frac{Vmax}{β} \)
The total time T is the sum of the acceleration time t1 and the deceleration time t2:
\( T = t1 + t2 \)
Substituting the expressions for t1 and t2:
\( T = \frac{Vmax}{α} + \frac{Vmax}{β} \)
Factoring out Vmax from the equation:
\( T = Vmax \left( \frac{1}{α} + \frac{1}{β} \right) \)
This can be rewritten as:
\( T = Vmax \cdot \frac{α + β}{αβ} \)
Now, we can solve for Vmax:
\( Vmax = \frac{T \cdot αβ}{α + β} \)
Thus, the maximum velocity acquired by the car is:
\( Vmax = \frac{αβ}{α + β} \cdot T \)
Topper's Solved these Questions
- MOTIONBOOK - MCGROW HILL PUBLICATIONCHAPTER - MOTIONEXERCISE - HIGHER ORDER THINKING QUESTIONS
48 Videos
- MISCELLANEOUS QUESTIONSBOOK - MCGROW HILL PUBLICATIONCHAPTER - MISCELLANEOUS QUESTIONSEXERCISE - PART-B
99 Videos
- REFLECTION OF LIGHT BOOK - MCGROW HILL PUBLICATIONCHAPTER - REFLECTION OF LIGHT EXERCISE - HIGHER ORDER THINKING QUESTIONS
10 Videos
Similar Questions
A car acceleration form rest at a constant rate α for some time, after which it decelerates at a constant rate β, to come to rest. If the total time elapsed is t evaluate (a) the maximum velocity attained and (b) the total distance travelled.
View SolutionA car accelerates from rest at a constant rate α for some time, after which it decelerates at a constant rate β, to come to rest. If the total time elapsed is t seconds. Then evalute (a) the maximum velocity reached and (b) the total distance travelled.
View Solution
Knowledge Check
A car accelerates from rest at a constant rate for some time after which it decelerates at a constant rate β to come to rest. If the total time elapsed is t, the maximum velocity acquired by the car is given by :
Aαβα+βtBα+βαβtCα2+β2βαDα+β2βαA car accelerates from rest at a constant rate for some time after which it decelerates at a constant rate β to come to rest. If the total time elapsed is t, the maximum velocity acquired by the car is given by :
Aab(a+b)tBab(a−b)tCat2(a+b)Dtb2(a+b)A car accelerates from rest at a constant rate of 2ms−2 for some time. The it retatds at a constant rate of 4ms−2 and comes to rest. It remains in motion for 6s.
AIts maximum speed is 8ms−1BIts maximum speed is 6ms−1CIt travelled a total distance of 24mDIt travelled a total distance of 18m
A car accelerates from rest at a constant rate α for some time, after which it decelerates at a constant rate β and ultimately comes to rest.If the total time-lapse is t, what is the total distance described and maximum velocity reached ?
View Solution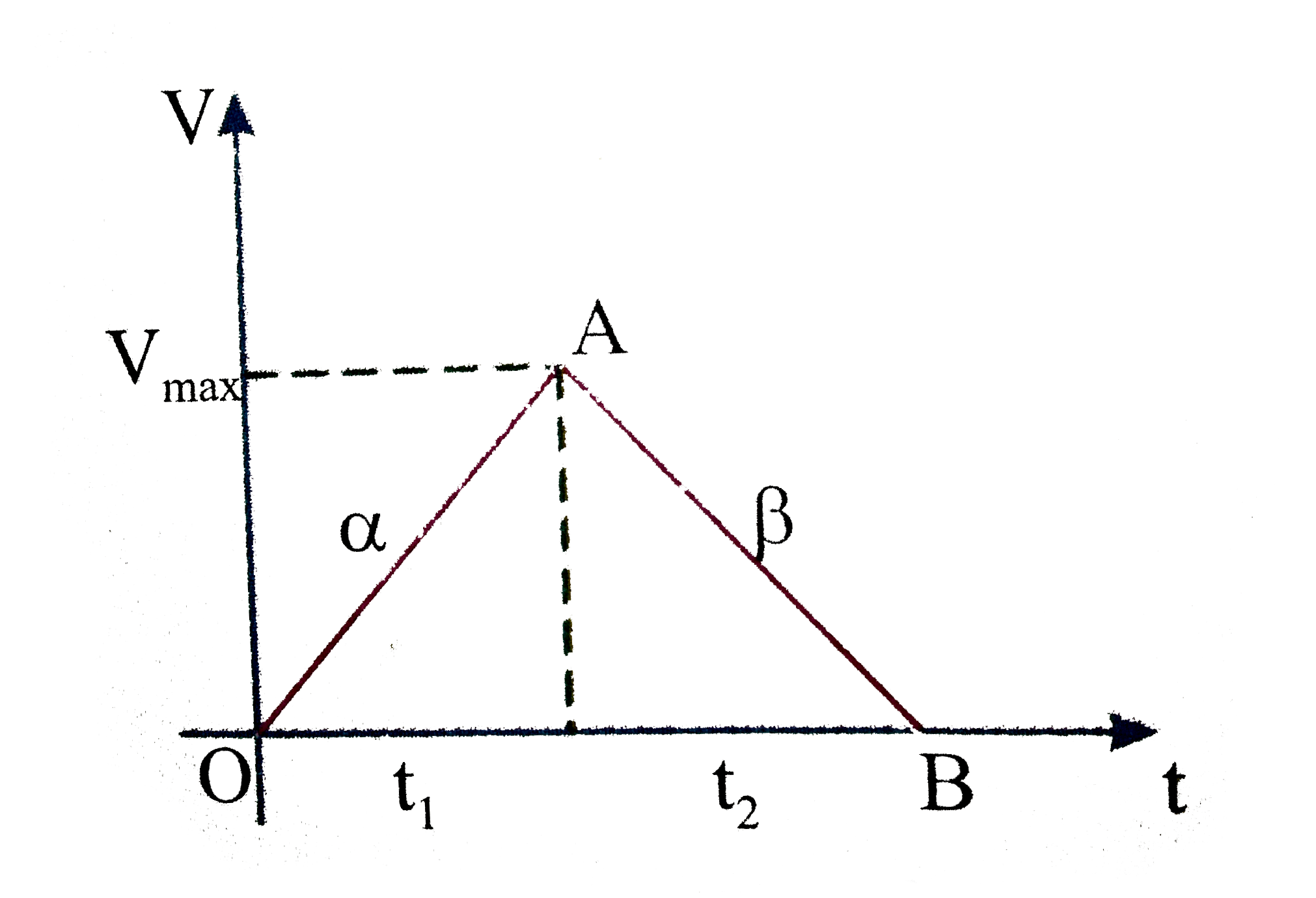
A bus accelerated from rest at a constant rate α for some time, after which it decelerates at a constant rate β to come to rest. If the total time elapsed is t seconds. Then evaluate following parameters from the given graph
(a) the maximum velocity achieved.
(b) the total distance travelled graphically and
(c) Average velocity.
View SolutionA particle accelerates from rest at a constant rate for some time and attains a velocity of 8 m/sec. Afterwards it decelerates with the constant rate and comes to rest. If the total time taken is 4 sec, the distance travelled is
View SolutionA car acceleration from rest at a constant rate 2m/s2 for some time. Then, it retards at a constant rate of 4m/s2 and comes to rest. If it remains motion for 3 second, then the maximum speed attained by the car is:-
View SolutionA car accelerates from rest at constant rate of 2ms−2 for some time. Then it retards at a constant rate of 4ms−2 and comes to rest. It remains in motion for 3 seconds
View Solution
