A car accelerates from rest at a constant rate α for some time, after which it decelerates at a constant rate β, to come to rest. If the total time elapsed is t seconds. Then evalute (a) the maximum velocity reached and (b) the total distance travelled.
The correct Answer is:A, B, C, D
To solve the problem step by step, we will evaluate both the maximum velocity reached by the car and the total distance traveled during the acceleration and deceleration phases.
Step 1: Understanding the Motion
The car accelerates from rest at a constant rate α for a time t1 and then decelerates at a constant rate β for a time t2 until it comes to rest. The total time of the journey is given as t=t1+t2.
Step 2: Finding Maximum Velocity
1. From A to B (Acceleration Phase):
- Initial velocity u=0
- Final velocity v=vmax
- Acceleration a=α
- Time t1
Using the first equation of motion:
vmax=u+αt1⟹vmax=0+αt1⟹vmax=αt1
2. From B to C (Deceleration Phase):
- Initial velocity u=vmax
- Final velocity v=0
- Deceleration a=−β
- Time t2
Using the first equation of motion:
0=vmax−βt2⟹vmax=βt2
3. Equating the Two Expressions for vmax:
From the two equations we derived:
αt1=βt2
4. Using Total Time:
Since t=t1+t2, we can express t2 in terms of t1:
t2=t−t1
5. Substituting for t2:
Substitute t2 into the equation αt1=βt2:
αt1=β(t−t1)
Rearranging gives:
αt1+βt1=βt⟹t1(α+β)=βt⟹t1=βtα+β
6. Finding t2:
Substitute t1 back to find t2:
t2=t−t1=t−βtα+β=αtα+β
7. Substituting Back to Find vmax:
Now substitute t1 into vmax:
vmax=αt1=α(βtα+β)=αβtα+β
Step 3: Finding Total Distance
1. Distance from A to B:
Using the equation of motion:
s1=ut+12at21=0+12αt21=12α(βtα+β)2
Simplifying gives:
s1=12αβ2t2(α+β)2
2. Distance from B to C:
Using the equation of motion:
s2=vmaxt2−12βt22
Substituting vmax and t2:
s2=αβtα+β⋅αtα+β−12β(αtα+β)2
Simplifying gives:
s2=αβt2(α+β)2−12βα2t2(α+β)2=(αβ−12α2)t2(α+β)2
3. Total Distance:
The total distance s is:
s=s1+s2=12αβ2t2(α+β)2+(αβ−12α2)t2(α+β)2
Combining gives:
s=t22(α+β)⎛⎝αβ+αβ−12α2(α+β)⎞⎠=t22(α+β)⎛⎝2αβ−12α2(α+β)⎞⎠
Final Answers
(a) The maximum velocity reached is:
vmax=αβtα+β
(b) The total distance traveled is:
s=t22(α+β)
The car accelerates from rest at a constant rate α for a time t1 and then decelerates at a constant rate β for a time t2 until it comes to rest. The total time of the journey is given as t=t1+t2.
1. From A to B (Acceleration Phase):
- Initial velocity u=0
- Final velocity v=vmax
- Acceleration a=α
- Time t1
Using the first equation of motion:
vmax=u+αt1⟹vmax=0+αt1⟹vmax=αt1
- Initial velocity u=vmax
- Final velocity v=0
- Deceleration a=−β
- Time t2
Using the first equation of motion:
0=vmax−βt2⟹vmax=βt2
From the two equations we derived:
αt1=βt2
Since t=t1+t2, we can express t2 in terms of t1:
t2=t−t1
Substitute t2 into the equation αt1=βt2:
αt1=β(t−t1)
Rearranging gives:
αt1+βt1=βt⟹t1(α+β)=βt⟹t1=βtα+β
Substitute t1 back to find t2:
t2=t−t1=t−βtα+β=αtα+β
Now substitute t1 into vmax:
vmax=αt1=α(βtα+β)=αβtα+β
1. Distance from A to B:
Using the equation of motion:
s1=ut+12at21=0+12αt21=12α(βtα+β)2
Simplifying gives:
s1=12αβ2t2(α+β)2
Using the equation of motion:
s2=vmaxt2−12βt22
Substituting vmax and t2:
s2=αβtα+β⋅αtα+β−12β(αtα+β)2
Simplifying gives:
s2=αβt2(α+β)2−12βα2t2(α+β)2=(αβ−12α2)t2(α+β)2
The total distance s is:
s=s1+s2=12αβ2t2(α+β)2+(αβ−12α2)t2(α+β)2
Combining gives:
s=t22(α+β)⎛⎝αβ+αβ−12α2(α+β)⎞⎠=t22(α+β)⎛⎝2αβ−12α2(α+β)⎞⎠
(a) The maximum velocity reached is:
vmax=αβtα+β
s=t22(α+β)
Topper's Solved these Questions
- KINEMATICSBOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - Example Type 1
1 Video
- KINEMATICSBOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - Example Type 2
1 Video
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises
45 Videos
- KINEMATICS 1BOOK - DC PANDEYCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
Similar Questions
A car acceleration form rest at a constant rate α for some time, after which it decelerates at a constant rate β, to come to rest. If the total time elapsed is t evaluate (a) the maximum velocity attained and (b) the total distance travelled.
View Solution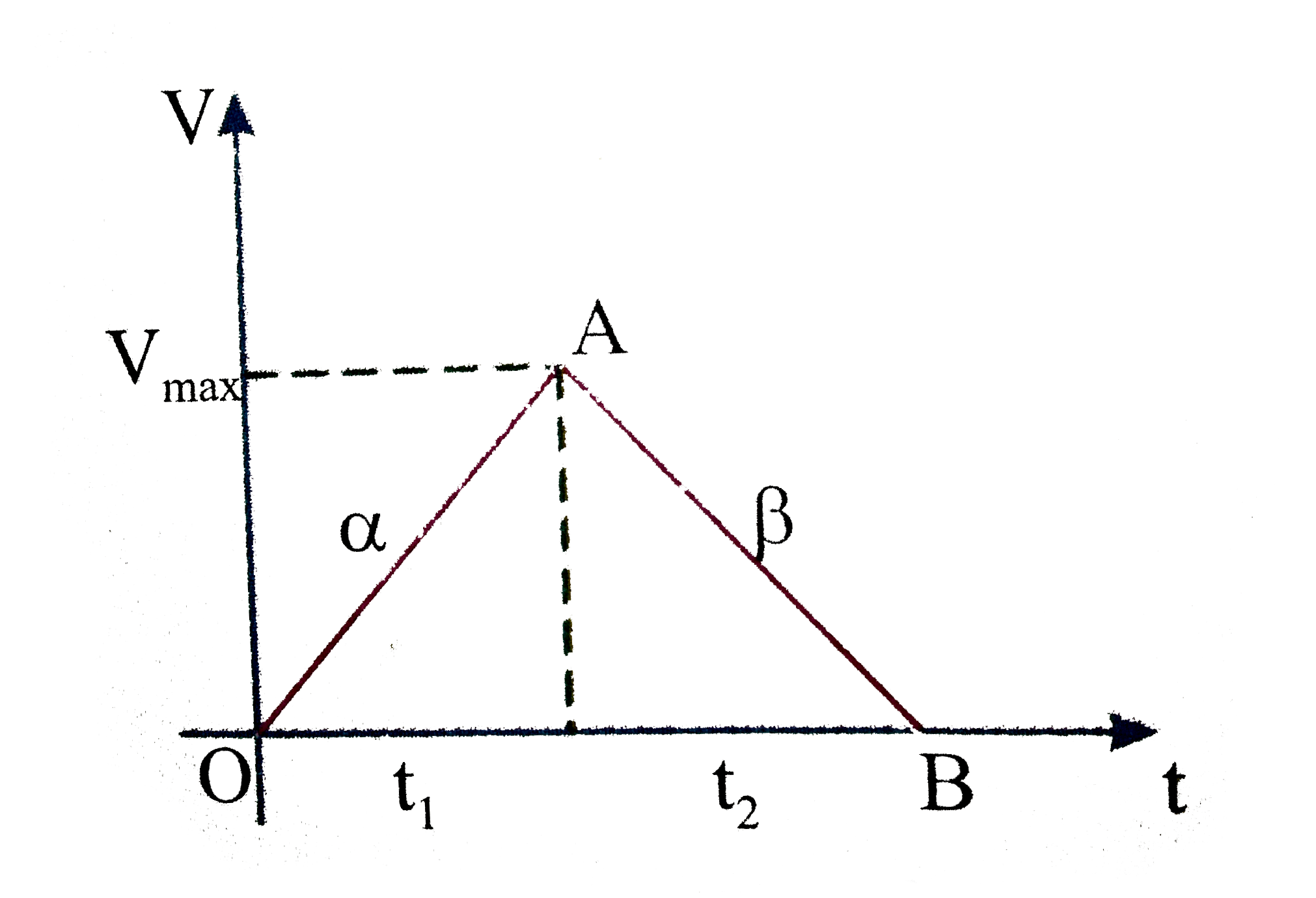
A bus accelerated from rest at a constant rate α for some time, after which it decelerates at a constant rate β to come to rest. If the total time elapsed is t seconds. Then evaluate following parameters from the given graph
(a) the maximum velocity achieved.
(b) the total distance travelled graphically and
(c) Average velocity.
View Solution
Knowledge Check
A car accelerates from rest at a constant rate for some time after which it decelerates at a constant rate β to come to rest. If the total time elapsed is t, the maximum velocity acquired by the car is given by :
Aab(a+b)tBab(a−b)tCat2(a+b)Dtb2(a+b)A car accelerates from rest at a constant rate for some time after which it decelerates at a constant rate β to come to rest. If the total time elapsed is t, the maximum velocity acquired by the car is given by :
Aαβα+βtBα+βαβtCα2+β2βαDα+β2βαA car accelerates from rest at a constant rate α for sometime , after which it decelerates at a constant rate β and comes to rest. If T is the total time elapsed, the maximum velocity acquired by the car is
A(αβα+β)TB((α+βαβ)TC(α2+β2αβ)TD12αTβ
A car accelerates from rest at a constant rate α for some time, after which it decelerates at a constant rate β and ultimately comes to rest.If the total time-lapse is t, what is the total distance described and maximum velocity reached ?
View SolutionA car accelerates from rest at acionstant rate 36kmh∘ to comet to rest. If the total time elapsed id 1 hour, calculate (i) the maximum velocity attained by the car and (ii) the total distance travelled by car.
View SolutionA particle accelerates from rest at a constant rate for some time and attains a velocity of 8 m/sec. Afterwards it decelerates with the constant rate and comes to rest. If the total time taken is 4 sec, the distance travelled is
View SolutionA car accelerates from rest at a constant rate of 2ms−2 for some time. The it retatds at a constant rate of 4ms−2 and comes to rest. It remains in motion for 6s.
View SolutionA car accelerates from rest at constant rate of 2ms−2 for some time. Then it retards at a constant rate of 4ms−2 and comes to rest. It remains in motion for 3 seconds
View Solution