Consider the points lying on a straight line joining two fixed opposite charges. Between the charges there is

No point where electric field is zero

Only one point where electric field is zero

No point where potential is zero

Only one point where potential is zero

Video Solution

Text Solution

Generated By DoubtnutGPT

To solve the problem regarding the electric field and electric potential between two fixed opposite charges, let's break it down step by step.
1. Understanding the Setup:
- We have two fixed charges: one positive charge $Q_{1}$ and one negative charge $Q_{2}$ (where $Q_{2} = - Q$ ).
- They are separated by a distance $d$ .
2. Electric Field Between the Charges:
- The electric field $E$ due to a point charge is given by the formula:
$E = \frac{k | Q |}{r^{2}}$
where $k$ is Coulomb's constant, $Q$ is the charge, and $r$ is the distance from the charge.
- In the region between the two charges, the electric field due to $Q_{1}$ (positive) points away from $Q_{1}$ and the electric field due to $Q_{2}$ (negative) points towards $Q_{2}$ .
3. Direction of Electric Fields:
- Since both electric fields are in the same direction (from the positive charge to the negative charge), they will add up.
- Therefore, the resultant electric field $E_{n e t}$ at any point between the charges is not zero:
$E_{n e t} = E_{Q_{1}} + E_{Q_{2}} > 0$
- This means there is no point between the charges where the electric field is zero.
4. Electric Potential Between the Charges:
- The electric potential $V$ at a point due to a charge is given by:
$V = \frac{k Q}{r}$
- The total potential $V_{n e t}$ at any point between the charges can be expressed as:
$V_{n e t} = V_{Q_{1}} + V_{Q_{2}} = \frac{k Q_{1}}{r_{1}} + \frac{k Q_{2}}{r_{2}}$
- Here, $r_{1}$ is the distance from $Q_{1}$ to the point and $r_{2}$ is the distance from $Q_{2}$ to the point.
5. Finding the Point Where Potential is Zero:
- Set the total potential to zero:
$V_{n e t} = \frac{k Q_{1}}{r_{1}} + \frac{k Q_{2}}{r_{2}} = 0$
- This leads to:
$\frac{Q_{1}}{r_{1}} + \frac{Q_{2}}{r_{2}} = 0$
- Rearranging gives:
$\frac{Q_{1}}{r_{1}} = - \frac{Q_{2}}{r_{2}}$
- This indicates that there is only one point between the charges where the potential is zero, which occurs when the magnitudes of the potentials due to each charge are equal.
6. Conclusion:
- Therefore, we conclude that:
- There is no point where the electric field is zero between the charges.
- There is only one point where the electric potential is zero.
Final Answer:
- No point where electric field is zero and only one point where potential is zero.

Updated on:18/9/2024

At any point on the right bisector of line joining two equal and opposite charges
Athe electric field is zero
Bthe electric potential is zero
Cthe electric potential decreases with increasing distance from centre
Dthe electric field is perpendicular to the line joining the charges
Two point charges are kept at a certain distance from one another. The graph represents the variartion of the potential along the straight line connecting the two charges. At what point is the electric field zero ?

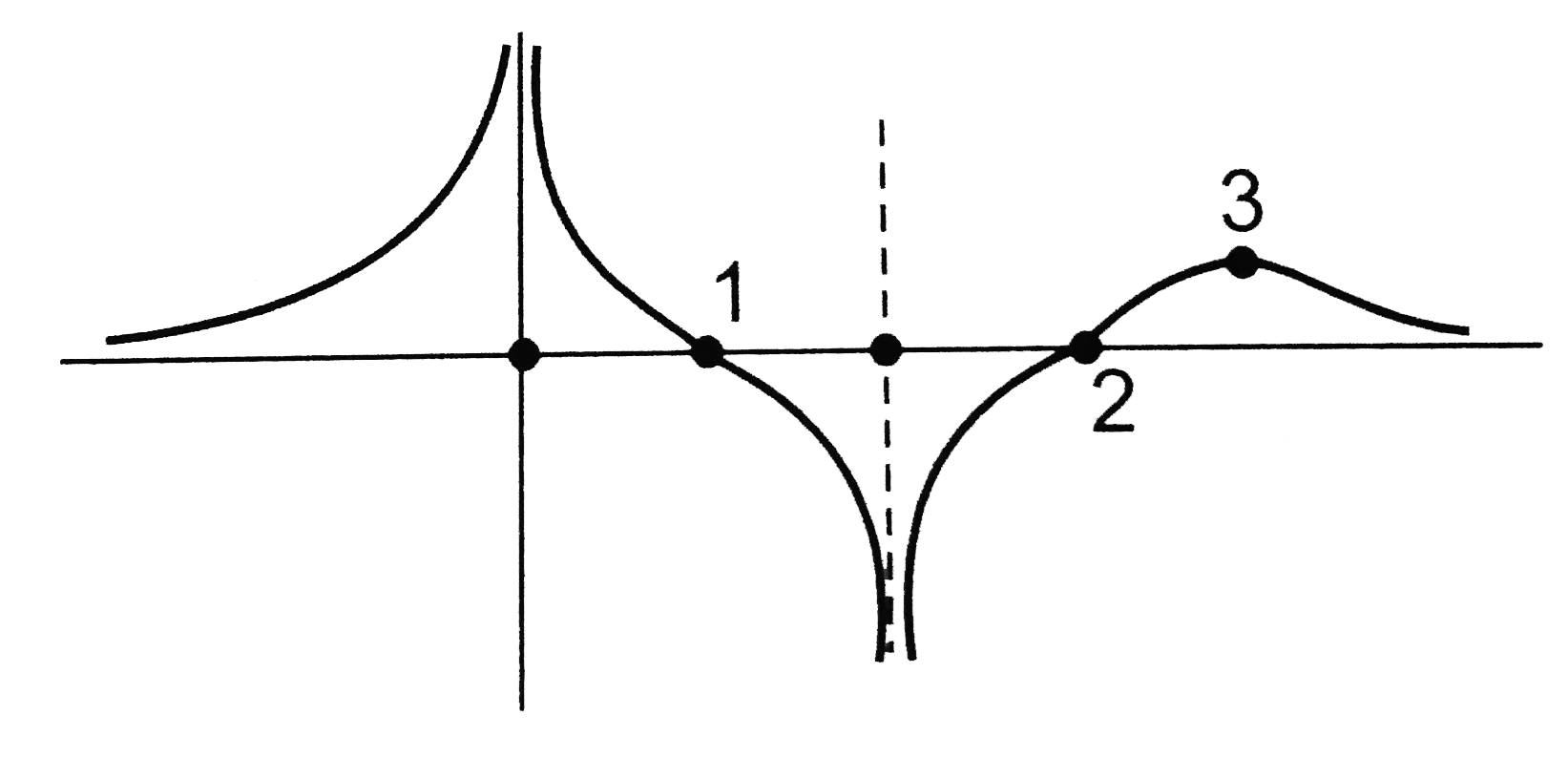A $1$
B $2$
C $3$
Dnone of these
A charge q is placed at the centre of the line joining two equal charges Q. The system of the three charges will be in equilibrium , if q is equal to
A $- \frac{Q}{2}$
B $- \frac{Q}{4}$
C $+ \frac{Q}{4}$
D $+ \frac{Q}{2}$