Verify mean value theorem for the function f(x)=x+1x in the interval [1,3] .Solution in Malayalam
Step by step video & image solution for Verify mean value theorem for the function f(x)=x+frac1x in the interval [1,3] . by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
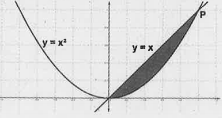
Consider the following figure
find the point of intersection (P) of the parabola and the line.
View SolutionUsing properties of determinants prove
∣∣ ∣ ∣∣xyx+yyx+yxx+yxy∣∣ ∣ ∣∣=−2(x3+y3)
View SolutionVerify Lagrange's Mean Value theorem for the following functions in the given intervals
f(x) = ex in the interval [0,1].
View SolutionVerify Lagrange's Mean Value theorem for the following functions in the given intervals
f(x) = tan−1x in the interval [0,1]
View Solutionअंतराल [2,4] में फलनf(x)=x2 के लिए माध्य्मान प्रमेय को सत्यापित कीजिए ।
View Solutionफलन f(x)=x−1x के लिए अंतराल [1,3] में लाग्रांज माध्य मान प्रमेय का सत्यापन कीजिए एव दिए गये अंतराल में c का मान ज्ञात कीजिए ।
View Solutionनिम्नलिखित फलनों व अंतरालों के लिए लैग्रांज के मध्यमान प्रमेय का सत्यापन कीजिएः
f(x)=x(x−2), अंतराल [1,3]
View Solutionनिम्नलिखित फलनों व अंतरालों के लिए लैग्रांज के मध्यमान प्रमेय का सत्यापन कीजिएः
f(x)=x+1x, अंतराल [1,3]
View Solutionनिम्नलिखित फलनों व अंतरालों के लिए लैग्रांज के मध्यमान प्रमेय का सत्यापन कीजिएः
f(x)=x−1x, अंतराल [1,3]
View SolutionA value of c for which the conclusion of Mean value Theorem holds for the function f(x)=logex on the interval [1,3] is
View SolutionA value of c for which the conclusion of Mean Value Theorem holds for the function f(x)=logex on the interval [1, 3] is
View SolutionConsider the function
f(x)=x(x−2) , x∈[1,3]
Verify mean value theorem for the function in [1,3] .
View SolutionC A value of f(x)=log_e x, Interval [1,3] The conclusion of the mean theorem is verified in
View SolutionVerify Lagrange's mean value theorem for the following functions: f(x)=x+(1x) on the interval (1,3)
View SolutionVerify Mean Value Theorem if f(x)=x3−5x2−3x in the interval [1,3].
View Solution
