Verify Rolle's theorem for the function
f(x)=x2+2 in the interval [-2,2]Solution in Malayalam
Step by step video & image solution for Verify Rolle's theorem for the function f(x)=x^2+2 in the interval [-2,2] by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
Similar Questions
Consider the following figure
find the point of intersection (P) of the parabola and the line.
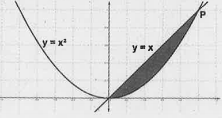 02:18View Solution
02:18View SolutionUsing properties of determinants prove
∣∣ ∣ ∣∣xyx+yyx+yxx+yxy∣∣ ∣ ∣∣=−2(x3+y3)01:47View SolutionVerify Rolle's theorem for the function f(x) = x2 in the interval [−1,1].
01:37View SolutionVerify Rolle's theorem for the following functions in the given intervals.
f(x) = x2 in the interval [−2,2].01:20View SolutionVerify Rolle's theorem for the following functions in the given intervals.
f(x) = x2−5x−6 in the interval [−1,6] .02:34View SolutionVerify Rolle's theorem for the following functions in the given intervals.
f(x) = x2−6x+8 in the interval [2,4].03:14View SolutionVerify Rolle's theorem for the following functions in the given intervals.
f(x) = x(x−4)2 in the interval [0,4].02:32View SolutionVerify Rolle's theorem for the following functions in the given intervals.
f(x) = sinx + cos x in the interval [0,π/2].04:56View SolutionVerify Rolle's theorem for the function f(x)=x2+2,x∈[−2,2]
06:35View SolutionVerify the truth of Rolle's Theorem for the following functions :
f(x)=(x−1)(x−2)2 in the interval [1, 2]04:52View SolutionVerify the truth of Rolle's Theorem for the following functions :
f(x)=(x−2)(x−4)2 in the interval [2, 4].02:42View SolutionVerify Rolle's theorem for the function f(x) = x2 in the interval [−1,1].
03:25View SolutionVerify Rolle's theorem for the following functions in the given intervals.
f(x) = x2 in the interval [−2,2].04:29View SolutionVerify Rolle's theorem for the following functions in the given intervals.
f(x) = x2−6x+8 in the interval [2,4].04:14View SolutionVerify Rolle's theorem for the following functions in the given intervals.
f(x) = x(x−4)2 in the interval [0,4].04:57View Solution

