If y=log(1x) , show that dydx+ey=0Solution in Malayalam
Step by step video & image solution for If y=log(1/x) , show that dy/dx+e^y=0 by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
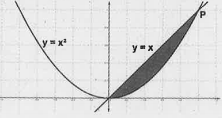
Consider the following figure
find the point of intersection (P) of the parabola and the line.
View SolutionUsing properties of determinants prove
∣∣ ∣ ∣∣xyx+yyx+yxx+yxy∣∣ ∣ ∣∣=−2(x3+y3)
View SolutionIf xy=ex−y, show that dydx=logx{log(xe)}2
View SolutionIf x^(y)=e^(x-y), then show that (dy)/(dx)=(log x)/((1+log x)^(2))
View SolutionIf yx=ey−x , prove that dydx=(1+logy)2logy
View SolutionIf y=eax Show that xdydx=ylogy.
View SolutionIf y= elog(logx),thendydx =
View SolutionIf x log xdydx+y=logx2 and y(e)=0 , then
y(e2)=
View SolutionIf xlogxdydx+y=logx2andy(e)=0, then y(e2)=
View SolutionIf y=exex...∞,show that,dydx=y2logyx(1−ylogxlogy).
View SolutionIf y=e[log(x+1)−logx]. Finddydx
View SolutionIf xy=ex−y, show that dydx=logx{log(xe)}2
View SolutionFind dydx:
x=ecos2tandy=esin2t show that, dydx=−ylogxxlogy
View SolutionIf y=elogx, show that dydx=1
View SolutionIf xy=ex−y, then show that dydx=logx(1+logx)2
View Solution

