Let f(x)=
Find the value of c if is continuous on .Solution in Malayalam
Step by step video & image solution for Let f(x)={(cosx,0lexlec),(sinx,c<xlepi)} Find the value of c if f is continuous on [0,pi] . by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Consider the following figure
find the point of intersection (P) of the parabola and the line.
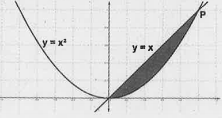
View SolutionUsing properties of determinants prove
∣∣ ∣ ∣∣xyx+yyx+yxx+yxy∣∣ ∣ ∣∣=−2(x3+y3)
View SolutionThe function f(x)=1−sinx+cosx1+sinx+cosx is not defined at x=π.
The value of f(π) so that f(x) is continuous at x=π is
View SolutionThe function f(x)=1−sinx+cosx1+sinx+cosx is not defined at x=π. The value of f(π), so that f(x) is continuous at x=π, is
View Solutionनिम्नलिखित फलनों के सांतत्य पर विचार कीजिए :
(a) f(x)=sinx+cosx
(b) f(x)=sinx−cosx
(c) f(x)=sinx.cosx
View SolutionFind the value of k for which the function
f(x)={kx+4when x≤πcosx when x>π,
is continuous at x=π .
View SolutionFind the value of k for which the function
f(x)={kx+2when x≤πcosx when x>π,
is continuous at x=π .
View SolutionIf the function f(x)={kx+1, if x≤πcosx, if x>π is continuous at x=π, then the value of 'k' is :
View SolutionIf f(x)=1+sinx−cosx1−sinx−cosx,x≠0 . The value of f(0) so that f is a continuous function is
View SolutionIf f(x)=√1−sin2x , then f′(x) is equal to
(a)−(cosx+sinx),for x∈(π4,π2)
(b)cosx+sinx ,for x∈(0,π4)
(c)−(cosx+sinx),for x∈(0,π4)
(d)cosx−sinx ,for x∈(π4,π2)
View SolutionLet F(x)=[cosx -sinx 0 sinx cosx 0 0 0 1].Show that F(x) F(y)=F(x+y)
View SolutionFind the value of k.
If f(x) = {kx+1, if x≤πcosx, if x>π is continuous at x=π.
View SolutionIf f(x)=∣∣ ∣∣sinxcosxsinxcosx−sinxcosxx11∣∣ ∣∣ find the value of 2[f'(0)]+[f'(1)]2
View SolutionThe function f(x)={sinxx+cosx,x≠0 and f(x) =k at x=0 is continuous at x=0 then find the value of k
View SolutionFind the value of k, so that the function defined by f(x)={kx+1, if x≤πcosx, if x>π is continuous at x=π.
View Solution

