A body of mass 'm' is placed on a rough inclined plane having coefficient of friction μs . The inclination of plane is given as 'θ'. Find how much force is required to pull the body along the plane. 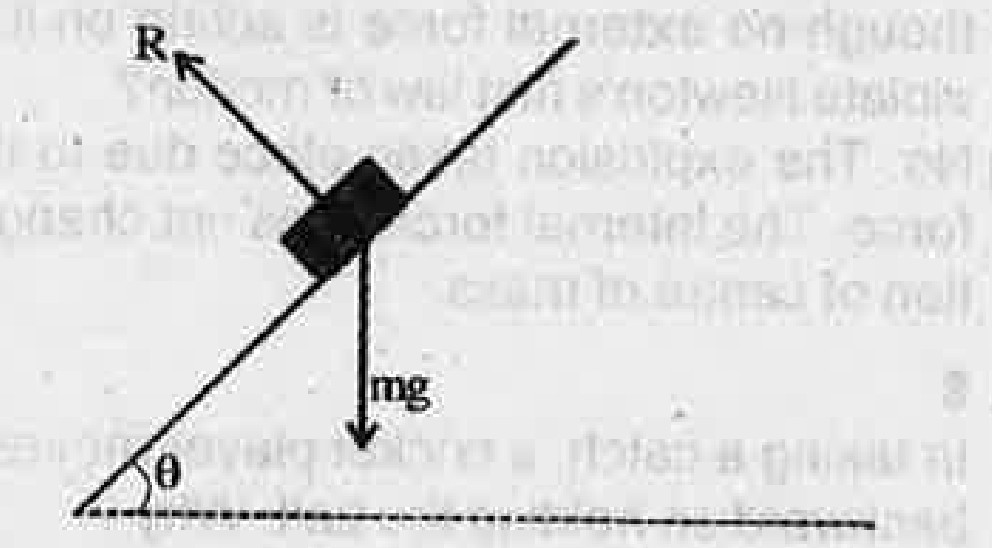 Solution in Malayalam
Solution in Malayalam
Step by step video & image solution for A body of mass 'm' is placed on a rough inclined plane having coefficient of friction mu_s . The inclination of plane is given as 'theta'. Find how much force is required to pull the body along the plane. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Why theoretical value does not agree with experimental value?
View SolutionWhen a surface is immersed in a liquid, what is the direction of pressure on the surface?
View SolutionA body of mass M is placed on a rough inclined plane of inclination theta and coefficient of friction mu_(k) A force of ( mg sin theta +mu_(k) mg cos theta ) is applied in the upward direction the acceleration of the body is .
View SolutionA body of mass 10 kg is lying on a rough inclined plane of inclination 37^(@) and mu = 1//2 , the minimum force required to pull the body up the plane is
View SolutionAn inclined plane is inclined at an angle theta with the horizontal. A body of mass m rests on it, if the coefficient of friction is mu , then the minimum force that has to be applied to the inclined plane to make the body just move up the inclined plane is
View SolutionA block of mass m is at rest on a rough inclined plane of angle of inclination θ. If coefficient of friction between the block and the inclined plane is μ, then the minimum value of force along the plane required to move the block on the plane is
View SolutionTo initiate an upward motion of a body along an inclined plane the minimum force required is twice the force required to keep the body at rest on the same incline . If the coefficient of friction is mu prove that the inclination of the plane is theta = tan^(-1) (3mu) .
View SolutionA body of mass M is placed on a rough inclined plane of inclination θ and coefficient of friction μk. A force of (mgsinθ+μkmgcosθ) is applied in the upward direction, the acceleration of the body is
View SolutionA body of mass 10kg is on a rough inclined plane having an inclination of 30° with the horizontal. If coefficient of friction between the surfaces of contact of the body and the plane is 0.5. Find the least force required to pull the body up the plane.
View SolutionA body of mass 10kg is on a rough inclined plane having an inclination of 30∘ with the horizontal. If coefficient of friction between the surfaces of contact of the body and the plane is 0.5. The least force required to pull the body up the plane is
View SolutionA body of mass 10kg is on a rough inclined plane having an inclination of 30∘ with the horizontal. If co-efficient of friciton between the surface of contact of the body and the plane is 0.25. Find the least force required to pull the body up.
View SolutionA body is placed on a rough inclined plane of inclination θ. As the angle θ to 90∘ the contact force between the block and the plane
View SolutionThe force required to move a body up a rough inclined plane is double the force required to prevent the body from sliding down the plane. The coefficient of friction when the angle of inclination of the plane is 60∘ is
View SolutionThe force required just to move a body up an inclined plane of angle of inclination θ is double the force required just to prevent the body sliding down. Find the coefficient of friction between the body and the plane.
View SolutionThe force required just to move a body up an inclined plane of angle of inclination theta is double the force required just to prevent the body sliding down. Find the coefficient of friction between the body and the plane.
View SolutionA body of mass 10kg is on a rough inclined plane having an inclination of 30∘ with the horizontal. If coefficient of friction between the surfaces of contact of the body and the plane is 0.5. The least force required to pull the body up the plane is
View Solution
