A solid sphere is thrown on a horizontal rough surface with initial velocity of centre of mass V0 without rolling. Velocity of its centre of mass when its starts pure rolling is
2V07
2V05
5V03
5V07
To solve the problem of finding the velocity of the center of mass of a solid sphere when it starts pure rolling after being thrown on a rough surface, we can follow these steps:
Step 1: Understand the Initial Conditions
The solid sphere is thrown with an initial velocity V0 and does not roll initially. Hence, the initial angular velocity ω0=0.
Step 2: Identify the Forces Acting on the Sphere
When the sphere is on the rough surface, the forces acting on it are:
- The gravitational force mg acting downwards.
- The normal force N acting upwards.
- The frictional force f acting in the direction opposite to the motion of the center of mass.
Step 3: Apply the Conservation of Angular Momentum
Since there is no net external torque acting about the point of contact (let's denote this point as point O), we can apply the conservation of angular momentum about point O.
The initial angular momentum Li about point O is given by:
Li=MV0r
where M is the mass of the sphere and r is its radius.
The final angular momentum Lf when the sphere starts rolling is given by:
Lf=MVr+Iω
where I is the moment of inertia of the sphere, and ω is its angular velocity. For a solid sphere, I=25Mr2.
Step 4: Relate Linear and Angular Velocities
When the sphere starts pure rolling, the relationship between linear velocity V and angular velocity ω is:
V=rω
Step 5: Set Up the Equation Using Conservation of Angular Momentum
Equating the initial and final angular momentum:
MV0r=MVr+25Mr2⋅Vr
This simplifies to:
MV0r=MVr+25MVr
Factoring out MVr:
MV0r=MVr(1+25)
MV0r=MVr⋅75
Step 6: Solve for the Final Velocity V
Cancelling M and r from both sides (assuming M≠0 and r≠0):
V0=V⋅75
Thus,
V=57V0
Final Answer
The velocity of the center of mass when the sphere starts pure rolling is:
V=57V0
---
The solid sphere is thrown with an initial velocity V0 and does not roll initially. Hence, the initial angular velocity ω0=0.
When the sphere is on the rough surface, the forces acting on it are:
- The gravitational force mg acting downwards.
- The normal force N acting upwards.
- The frictional force f acting in the direction opposite to the motion of the center of mass.
Since there is no net external torque acting about the point of contact (let's denote this point as point O), we can apply the conservation of angular momentum about point O.
Li=MV0r
where M is the mass of the sphere and r is its radius.
Lf=MVr+Iω
where I is the moment of inertia of the sphere, and ω is its angular velocity. For a solid sphere, I=25Mr2.
When the sphere starts pure rolling, the relationship between linear velocity V and angular velocity ω is:
V=rω
Equating the initial and final angular momentum:
MV0r=MVr+25Mr2⋅Vr
This simplifies to:
MV0r=MVr+25MVr
Factoring out MVr:
MV0r=MVr(1+25)
MV0r=MVr⋅75
Cancelling M and r from both sides (assuming M≠0 and r≠0):
V0=V⋅75
Thus,
V=57V0
The velocity of the center of mass when the sphere starts pure rolling is:
V=57V0
Topper's Solved these Questions
Similar Questions
A disc rolls without slipping on a horizontal surface such that its velocity of center of the mass is v. Find the velocity of points A,B,C and D.
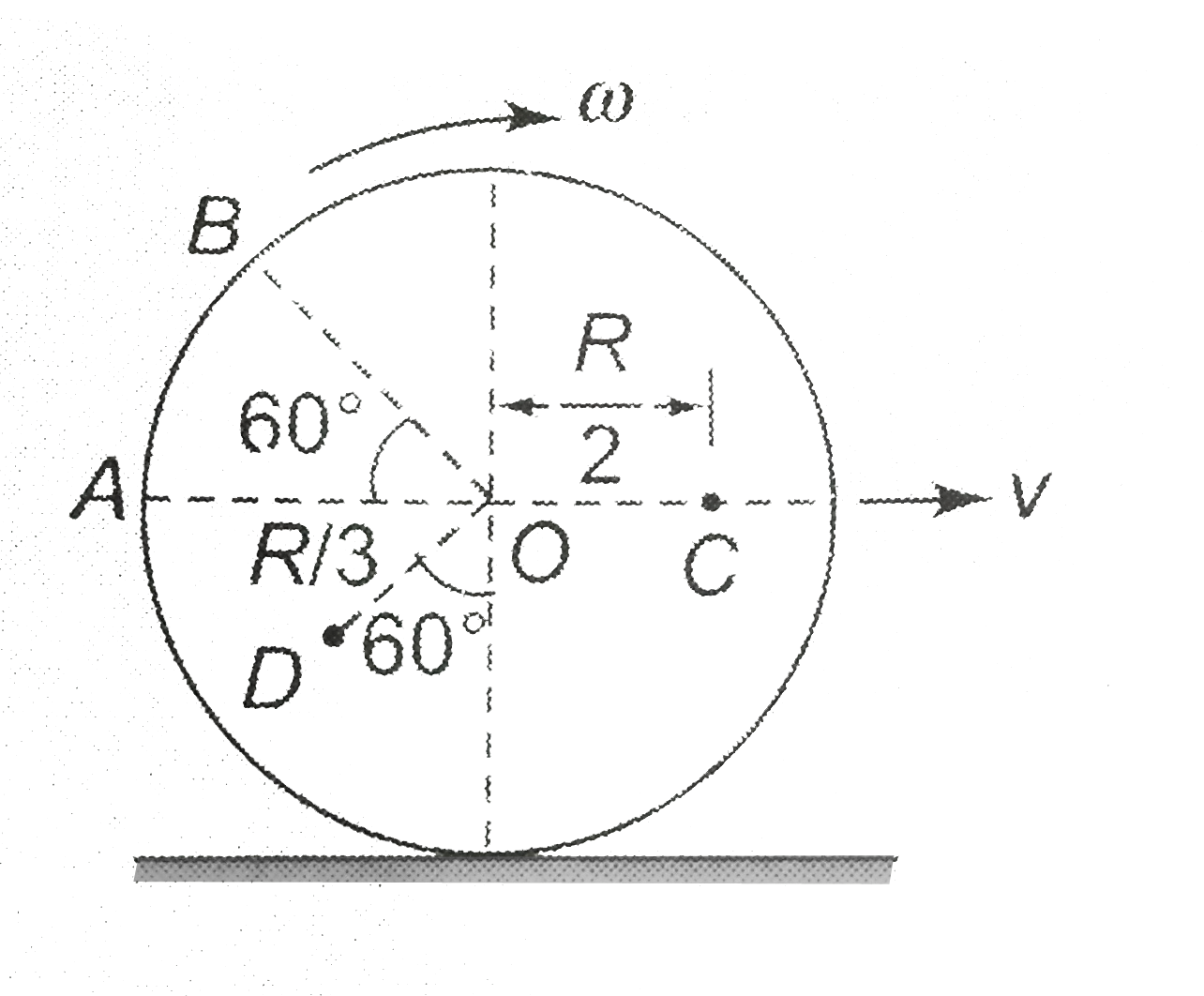
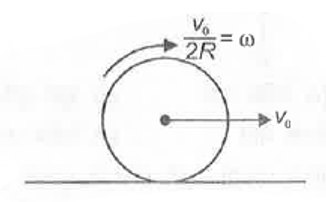
View SolutionA solid sphere has combined linear and rotation motion as shown in figure. The velocity of its centre of mass when it starts pure rolling is (R = radius of sphere)
View Solution
Knowledge Check
A uniform ring of radius R is given a back spin of angular velocity V0/2R and thrown on a horizontal rough surface with velocity of centre to be V0. The velocity of the centre of the ring when it starts pure rolling will be
AV02BV04C3V04D0A heavy solid sphere is thrown on a horizontal rough surface with initial velocity u without rolling. What will be its speed, when it starts pure rolling motion ?
A3u5B2u5C5u7D2u7If the velocity of centre of mass of a rolling body is V then velocity of highest point of that body is
A√2VBVC2VDV√2
If V is velocity of centre of mass of a rolling body then velocity of lowest point of that body is
View SolutionA hoop of radius r mass m rotating with an angular velocity ω0 is placed on a rough horizontal surface. The initial velocity of the centre of the hoop is zero. What will be the velocity of the centre of the hoop when it cases to slip ?
View SolutionA hoop of radius r and mass m rotating with an angular velocity ω0 is placed on a rough horizontal surface. The initial velocity of the centre of the hoop is zero. What will be the velocity of the centre of the hoop when it ceases ot slip?
View SolutionA wheel rolls without slipping on a horizontal surface such that its velocity of center of mass is v. The velocity of a particle at the highest point of the rim is
View SolutionA solid sphere of mass m= 500gm is rolling without slipping on a horizontal surface. Find kinetic energy of a sphere if velocity of centre of mass is 5 cm/sec
View Solution

