In the above problem the angular velocity of the system after the particle sticks to it will be?
0.3 rad/s
5.3 rad/s
10.3 rad/s
89.3 rad/s
The correct Answer is:C
Initial angular momentum of bullet + initial angular momentum of cylinder = Final angular momentum of (bullet+ cylinder) system
rad/sec.
Topper's Solved these Questions
- ROTATIONAL MOTIONBook:ERRORLESS Chapter:ROTATIONAL MOTIONExercise:Practice Problems (Problems based on centre of mass)
Explore 12 Videos
- ROTATIONAL MOTIONBook:ERRORLESS Chapter:ROTATIONAL MOTIONExercise:Practice Problems (Problems based on angular displacement, velocity and acceleration)
Explore 16 Videos
- NEWTONS LAWS OF MOTIONBook:ERRORLESS Chapter:NEWTONS LAWS OF MOTIONExercise:Self Evaluation Test
Explore 16 Videos
- SIMPLE HARMONIC MOTIONBook:ERRORLESS Chapter:SIMPLE HARMONIC MOTIONExercise:simple Harmonic Motion
Explore 21 Videos
Similar Questions
Knowledge Check
In the above problem the final angular velocity of the small cylinder is
Aω04Bω0Cω02Dω08In the above problem the root mean square velocity is
A4 m/sB3.01 m/sC3 m/sD5 m/sIn the above problem the velocity of the centre of mass after 1sec will be :
A203m/s vertically downB203m/s vertically upC703m/s vertically downD703m/s vertically up.
A uniform disc of mass m and radius R rotates about a fixed vertical axis passing through its centre with angular velocity ω. A particle of same angular velocity mass m and moving horizontally with velocity 2ωR towards centre of the disc collides and sticks to its rim.
The angular velocity of the disc after the particle sticks to it is
View SolutionIn the above question, the angular velocity will:
View Solution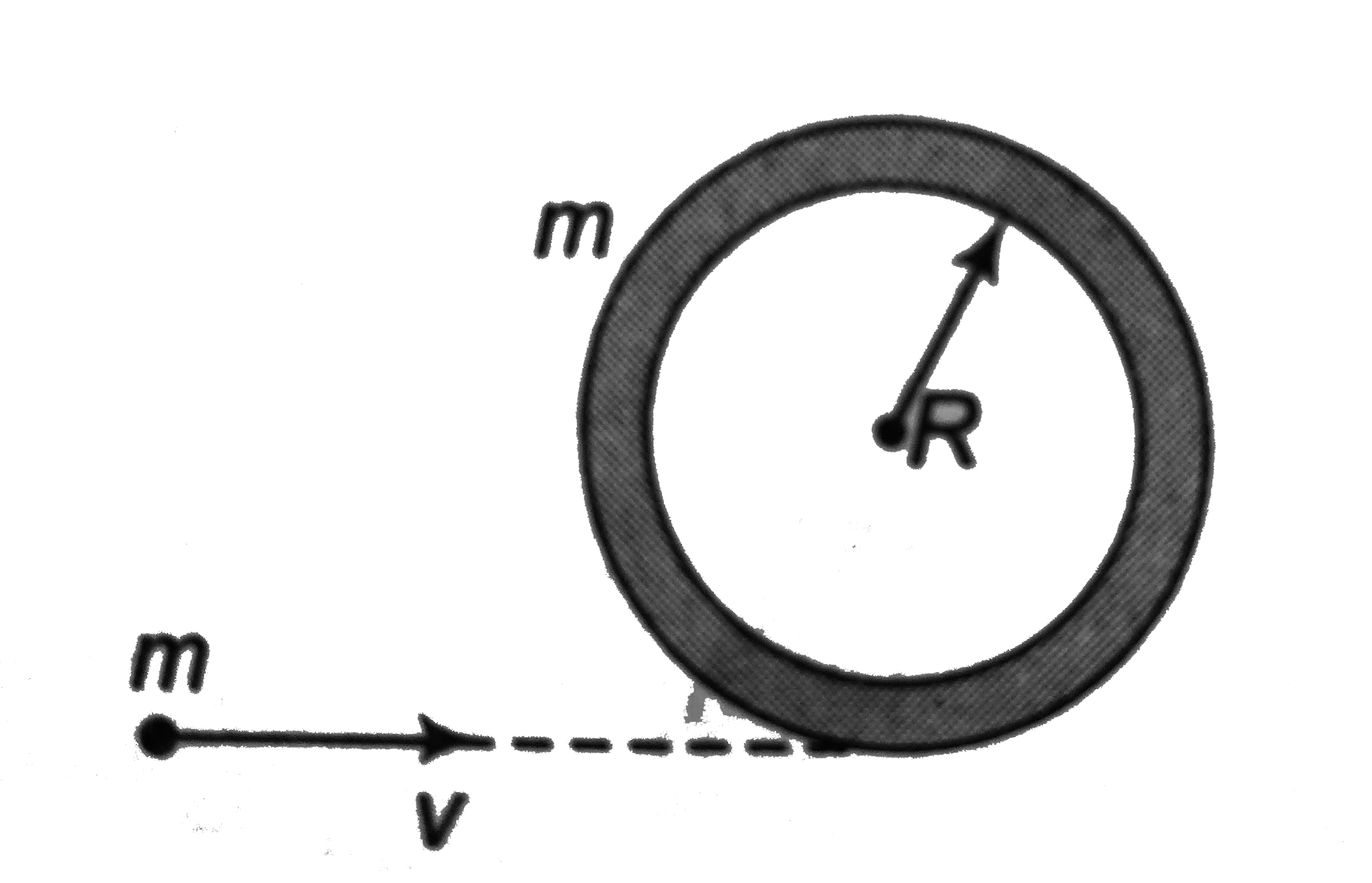
A circular ring of mass m and radius R rests flat on a horizontal smooth surface as shown in figure. A particle of mass m, and moving with a velocity v. Collides inelastically (e=0) with the ring the angular velocity with which the system rotates after the particle strikes the ring is
View SolutionA bar of mass 'm' length 'l' is in pure translatory motion with its centre velocity 'v' It collides with another identical bar which is in rest and sticks to it.
Assume that after the collision it becomes one system, then the angular velocity of the system after the collision is.
 .
.
View SolutionA bar of mass 'm' length 'l' is in pure translatory motion with its centre velocity 'v' It collides with another identical bar which is in rest and sticks to it.
Assume that after the collision it becomes one system, then the angular velocity of the system after the collision is.
 .
.
View Solution
