SI/MKSA मात्रक प्रणालियों के अतिरिक्त मात्रको की एक अन्य उपयोगी मात्रक प्रणाली है जिसे cgs (सेंटीमीटर-ग्राम-सेकण्ड) प्रणाली कहते है। इस प्रणाली के अनुसार कूलॉम-नियम इस प्रकार व्यक्त किया जाता है:
F=Qqr2ˆr
यहाँ दूरी r को cm(=10−2m)F, को डाइन (=10−5N) तथा आवेशों को स्थिर वैद्युत मात्रको (es मात्रको), यहां आवेश का मात्रक les है। =1[3]×10−9C समीकरण में संख्या [3] वास्तव में प्रकाश की चाल, के कारण जिसका यथार्थ मान अब C=2.99792458×108m/s लिया जाता है, आई है।
(i) यह दर्शाइए कि cgs में कूलॉम-नियम के अनुसार
1 esu आवेश = 1 (डाइन)1/2 सेन्टीमीटर
द्रव्यमान M, लम्बाई L तथा समय T के पदों में आवेश की विमाएँ प्राप्त कीजिए। यह दर्शाइए कि इसे M तथा L की भिन्नात्मक घातो के पदों में व्यक्त किया जाता है।
(ii) 1 esu आवेश = x C लिखिय, यहाँ x कोई विमाहीन संख्या है। यह दर्शाइए कि इससे यह प्राप्त होता है कि
14π∈0=10−9x2N.m2C2
जिसमे x=1[3]×10−9
अथवा 14π∈0=[3]2×109Nm2C2
14π∈0=(2.99792458)2×109Nm2C2 (यथार्थ)
(i) F=Qqr2=1 डाइन =[1 esu आवेश]2[1cm]2
अथवा
1 esu आवेश = 1 (डाइन)1/2(cm)
अतः [1 esu आवेश] =[F]1/2L=[MLT−2]1/2L=M1/2L3/2T−1
[1 esu आवेश] =M1/2L3/2T−1
इस प्रकार cgs मात्रको में आवेश को M की 1/2 तथा L की 3/2 की भिन्नात्मक घातो में व्यक्त किया जाता है।
(ii) दो आवेशों, जिनमे प्रत्येक का परिमाण 1 esu आवेश तथा जिनके बीच पृथकन 1 cm के बीच बल पर विचार कीजिए।
तब बल 1 डाइन =10−5N.
यह स्थिति 10−2m पृथकन वाले xC परिणाम के दो आवेशों के तुल्य है।
इससे प्राप्त होता है:
F=14π∈0.x210−4
जो होना चाहिए 1 डाइन =10−5N
इस प्रकार 14πε0.x210−4=10−5⇒14πε0=10−9x2Nm2C2
जिसके साथ x=1[3]×109, इससे प्राप्त होता है
14πε0=10−9×[3]2×1018=[3]2×109Nm2C2
जिसके साथ [3]→2.99792458, हमे प्राप्त होता है
14πε0=8.98755...×109Nm2C2 तथ्यतः
Topper's Solved these Questions
- वैद्युत आवेश तथा क्षेत्र BOOK - NCERT EXEMPLAR HINDICHAPTER - वैद्युत आवेश तथा क्षेत्र EXERCISE - लघुउत्तरीय (SA)
6 Videos
- विद्युतचुम्बकीय प्रेरणBOOK - NCERT EXEMPLAR HINDICHAPTER - विद्युतचुम्बकीय प्रेरणEXERCISE - दीर्घउत्तरीय (LA)
10 Videos
- संचार व्यवस्थाBOOK - NCERT EXEMPLAR HINDICHAPTER - संचार व्यवस्थाEXERCISE - दीर्घउत्तरीय (LA)
11 Videos
Similar Questions
कोई सिक्का Al−Mg मिश्रातु का बना है और इसका भार 0.75g है। यह वर्गाकार है तथा इसके विकरणों की माप 17 mm है। यह वैद्युत उदासीन है तथा इसमें धन और ऋण आवेश समान मात्रा में है।
यह मानते हुए कि पैसे के सिक्के केवल Al के बने है, धन तथा ऋण आवेशों की समान संख्याओं के परिमाण ज्ञात कीजिए। इस परिमाण से आप क्या निष्कर्ष निकालते है?
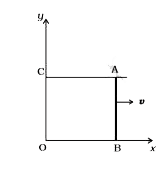
View Solutionकोई चुम्बकीय क्षेत्र B=B0sin(ωt)ˆk किसी विशाल प्रदेश पर आच्छादित है जिसमें तार AB ऐसे दो समांतर चालकों पर निर्बाध सरकता है जो एक दूसरे से d दूरी द्वारा पृथक्कृत है। ये तार x-y तल में है । तार AB (लम्बाई d की) का प्रतिरोध R है तथा समांतर चालकों (तारों) का प्रतिरोध उपेक्षणीय है। यदि AB v वेग से गमन करता है तो परिपथ में कितनी धारा है? तार को नियत वेग से गमन करने के लिए कितने बल की आवश्यकता है?
View Solutionकिसी संचार चैनल के अनुदिश गतिशील प्रकाश स्पन्द की तीव्रता, दूरी के साथ चरघातांकी रूप से, निम्न संबंध के अनुसार घटती है, I=I0e−αx जहाँ I0.x=0 पर तीव्रता है तथा α क्षीणन नियतांक है। दिखाइये कि (In4α) दूरी तय करने के पश्चात् तीव्रता में 75% की कमी आ जाती है।
View Solutionएक निर्माणकर्ता का मानना है की पुरुष और महिला मजदूरों की दक्षता समान होती है| अतएव वह उन्हें एक ही दर से मजदूरी देता है| उसके पास 30 मात्रक (units ) मजदूर और 17 मात्रक पूंजी है| जिसका वह A और B दो प्रकार के माल के उत्पादन में प्रयोग करते है|A के एक मात्रक उत्पादन में 2 मजदूर और 3 मात्रक पूंजी आवश्यकता है, जबकि B के एक मात्रक उत्पादन में 3 मजदूर और 1 मात्रक पूंजी आवश्यक है| A के एक मात्रक का मूल्य रु 100 तथा B के एक मात्रक का मूल्य रु 120 है | वह अपने साधनो का उपयोग किस प्रकार करें ताकि अधिकतम आय हो? क्या आप निर्माणकर्ता के इस दृष्टिकोण (विचार) से सहमत है की पुरुष और महिला मजदूरों की क्षमता समान होती है अतएव उन्हें एक ही दर से मजदूरी देनी चाहिए?
View Solutionपरवलय y=x2−2x+5 की जीवा दो बिन्दुओं जिनकी कोटि है, x1=1,x2=3 को जोड़ती है, तो इस जीवा के है, को जोड़ती है , तो इस जीवा के समान्तर परवलर की स्पर्श रेखा का समीकरण होगा
View Solutionमात्रको की अन्तराष्ट्रीय प्रणाली |OMR|Summary
View Solutionश्रवण कौशल को विकसित करने के लिए उपयुक्त प्रणाली है
View SolutionIn a certain code system, ‘how are you’ is coded as ‘639’, ‘are you fine today’ is coded as ‘6453’ and ‘stay fine’ is coded as ‘58’. What is the code for ‘ today’ in this system? एक निश्चित कोड प्रणाली में , ‘how are you’ ’को, 639’ के रूप में कोडित किया जाता है, ‘are you fine today’ को ‘6453’ ’के रूप में कोडित किया गया हैऔर ‘stay fine’ को ’58’ के रूप में कोडित किया गया है। इस प्रणाली में ‘ today’ के लिए कोड क्या है?
View SolutionSI पद्धति के मूल मात्रको की परिभाषाए
View Solutionपदार्थ A और B के बीच अभिक्रिया को निम्न प्रकार दर्शाया गया है
A+B−→C इस अभिक्रिया की दर से निम्न प्रेक्षणों को प्राप्त किया जाता है

View Solution2 N HCI के 25 ml, 4 N HNO_3 के 50 ml और 2 M H_2SO_4 के v ml को एक साथ मिलाया जाता है और कुल आयतन को 1 L तक तैयार किया जाता है, तनुकरण के बाद इस अम्ल मिश्रण का 50 ml, 1 N Na_2CO_3 के 25 ml के साथ पूर्णतया अभिक्रिया करता है। v का मान है
View Solutionजब AgNO_(3) के विलयन को आधिक्य में CoCl_(3).XNH_(3) विलयन के 1M में मिलाया जाता है, तो AgCI के एक मोल का निर्माण होता है? 'X' का मान क्या है? (माना लीजिए कि उपसहसंयोजन संख्या 6 है।)
View Solution1M Br_2 के एक 10 मिलीलीटर जलीय विलयन में NaOH का आधिक्य मिलाया जाता है, ताकि सभी Br_2, Br^(-) और BrO_3^(-) में विषमानुपातित हो जाए। निष्कर्षण द्वारा परिणामी विलयन को Br^(-) से मुक्त किया जाता है और विलयन को अम्लीकृत करके OH^(-) के आधिक्य को उदासीन कर दिया जाता है। परिणामी विलयन, अशुद्ध CaC_2O_4 (M = 128 ग्राम/मोल) नमूने के 2 ग्राम के साथ अभिक्रिया करने के लिए पर्याप्त है। निम्नलिखित में से ऑक्सैलेट नमूने की सही % शुद्धता कौनसी है?
View Solutionक्लोरीन मोनोऑक्साइड मूलक का क्लोरीन सिरा +0.167e का आवेश वहन करता है। बंध की लम्बाई 154.6 pm है। डिबाई मात्रक में मूलक के द्विध्रुव आघूर्ण की गणना कीजिए।
View Solutionसंगलित अशुद्ध धातु को लकड़ी के हरे रंग के लट्टे के साथ हिलाकर फफोलेदार तांबा को परिष्कृत किया जाता है, क्योंकि इस प्रकार की लकड़ी, हाइड्रोकार्बन गैसों (जैसे CH_4 ) को मुक्त करती है। इस प्रक्रम X को ________ कहा जाता है और इसका उपयोग धातु में प्रारंभ में उपस्थित Y की अशुद्धियों के शुद्धिकरण के लिए किया जाता है। Y _______ है।
View SolutionA+2BtoC , अभिक्रिया के लिए दर समीकरण इस प्रकार है: दर =k[A][B] यदि A की सांद्रता को समान रखा जाता है, लेकिन B की सांद्रता को दोगुना कर दिया जाता है, तो इसकी दर में क्या परिवर्तन होगा?
View Solution
