प्रश्न 1.20 में वर्णित एक सिक्के पर विचार कीजिए। यह वैद्युत उदासीन है तथा इसमें समान परिमाण, 34.8kc के धन तथा ऋण आवेश है। यदि ये आवेश दो बिन्दु आवेशों में सांद्रित है, जिनका पृथकन (i) 1cm (~12× पैसे के सिक्के का विकर्ण), (ii) 100m (~ किसी बड़े भवन की लम्बाई), तथा (ii) 106m (पृथ्वी की त्रिज्या) हो तो, तीन प्रकरणो में प्रत्येक के लिए इस प्रकार के बिन्दु आवेश पर बल ज्ञात कीजिए। इन परिणामो से आप क्या निष्कर्ष निकालते है?
F1=|q|24πε0r21=(8.99×109Nm2C2)(3.48×104C)10−4m2=1.1×1023N
F2F1=r21r22=(10−2m)2(102m)2=10−8⇒F2=F1×10−8=1.1×1015N
F3F1=r21r23=(10−2m)2(106m)2=10−16
F3=10−16F1=1.1×107N.
Topper's Solved these Questions
- वैद्युत आवेश तथा क्षेत्र Book:NCERT EXEMPLAR HINDIChapter:वैद्युत आवेश तथा क्षेत्र Exercise:दीर्घउत्तरीय (LA)
Explore 6 Videos
- वैद्युत आवेश तथा क्षेत्र Book:NCERT EXEMPLAR HINDIChapter:वैद्युत आवेश तथा क्षेत्र Exercise:अति लघुउत्तरीय (VSA)
Explore 6 Videos
- विद्युतचुम्बकीय प्रेरणBook:NCERT EXEMPLAR HINDIChapter:विद्युतचुम्बकीय प्रेरणExercise:दीर्घउत्तरीय (LA)
Explore 10 Videos
- संचार व्यवस्थाBook:NCERT EXEMPLAR HINDIChapter:संचार व्यवस्थाExercise:दीर्घउत्तरीय (LA)
Explore 11 Videos
Similar Questions
सन 1959 में लाइटलेटन एवं बॉण्डी ने सुझाया कि यदि द्रव्य पर कोई नेट आवेश हो तो विश्व (यूनिवर्स), के प्रसरण की व्याख्या की जा सकती है। जिनका संख्या घनत्व N है और जिसे और जिसे नियत रखा जाता है, मान लीजिए प्रोटॉन पर आवेश ep=−(1+y)e है, यहाँ e इलेक्ट्रॉनिक आवेश है।
(a) y का वह क्रांतिक मान ज्ञात कीजिए, जिस पर प्रसरण आरम्भ हो सके।
(b) यह दर्शाइए कि प्रसरण का वेग केन्द्र से दूरी के वर्ग के अनुक्रमानुपाती है।
View Solutionकिसी यादृच्छिक पृष्ठ में कोई द्विध्रुव परिबद्ध है। इस पृष्ठ से गुजरने वाला विद्युत फ्लक्स कितना है?
View Solutionकोई चुम्बकीय क्षेत्र B=B0sin(ωt)ˆk किसी विशाल प्रदेश पर आच्छादित है जिसमें तार AB ऐसे दो समांतर चालकों पर निर्बाध सरकता है जो एक दूसरे से d दूरी द्वारा पृथक्कृत है। ये तार x-y तल में है । तार AB (लम्बाई d की) का प्रतिरोध R है तथा समांतर चालकों (तारों) का प्रतिरोध उपेक्षणीय है। यदि AB v वेग से गमन करता है तो परिपथ में कितनी धारा है? तार को नियत वेग से गमन करने के लिए कितने बल की आवश्यकता है?
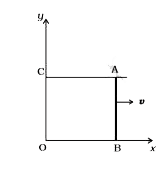
View Solutionकिसी संचार चैनल के अनुदिश गतिशील प्रकाश स्पन्द की तीव्रता, दूरी के साथ चरघातांकी रूप से, निम्न संबंध के अनुसार घटती है, I=I0e−αx जहाँ I0.x=0 पर तीव्रता है तथा α क्षीणन नियतांक है। दिखाइये कि (In4α) दूरी तय करने के पश्चात् तीव्रता में 75% की कमी आ जाती है।
View Solutionएक कम्पनी दो प्रकार के टेलीफ़ोन A व B बनाती है|A प्रकार के टेलीफ़ोन बनाने में 2 घण्टे एवं 300 टेलीफोनों को एक दिन में पैक किया जा सकता है| A प्रकार के टेलीफ़ोन का विक्रय मूल्य रु 300 तथा B प्रकार के टेलीफ़ोन का विक्रय मूल्य रु 400 है| अधिकतम लाभ के लिए कम्पनी A प्रकार के x तथा B प्रकार के y टेलीफ़ोन का निर्माण करती है तो रेखीय प्रतिबन्ध (x≥0,y≥0 के अलावा ) है:
View Solutionएक कम्पनी दो प्रकार के टेलीफोन A व B बनाती है | A प्रकार के टेलीफ़ोन बनाने में 2 घंटे एवं B प्रकार के टेलीफ़ोन बनाने में 4 घंटे लगते हैं |कम्पनी के पास 800 घंटे कार्य उपलब्ध है| 300 टेलीफोनों को एक दिन में पैक किया जाता है | A प्रकार के टेलीफोन का विक्रय मूल्य ₹300 तथा B प्रकार के टेलीफ़ोन का विक्रय मूल्य ₹400 है | अधिकतम लाभ के लिए कम्पनी A प्रकार के x तथा B प्रकार के y टेलीफोन का निर्माण करती है तो रेखीय प्रतिबंध के (x≥0,y≥0 अलावा ) है :
उपयुक्त प्रश्न के रेखीय कार्य योजना का सम्भाव्य क्षेत्र के निम्न प्रकार का है:
View Solutionएक कम्पनी दो प्रकार के टेलीफोन A व B बनाती है | A प्रकार के टेलीफ़ोन बनाने में 2 घंटे एवं B प्रकार के टेलीफ़ोन बनाने में 4 घंटे लगते हैं |कम्पनी के पास 800 घंटे कार्य उपलब्ध है| 300 टेलीफोनों को एक दिन में पैक किया जाता है | A प्रकार के टेलीफोन का विक्रय मूल्य ₹300 तथा B प्रकार के टेलीफ़ोन का विक्रय मूल्य ₹400 है | अधिकतम लाभ के लिए कम्पनी A प्रकार के x तथा B प्रकार के y टेलीफोन का निर्माण करती है तो रेखीय प्रतिबंध के (x≥0,y≥0 अलावा ) है :
उपयुक्त प्रश्न का अनुकूलतम है निम्नलिखित शीर्ष पर है|
View Solutionउन दो सरल रेखाओं के समीकरण ज्ञात कीजिए जो बिन्दु (0,a) से होकर जाती है तथा जिन पर बिन्दु (2a,2a) से खींचे गए लम्बो की माप a है।
View Solutionयदि शब्द PROBABILITY के अक्षर एक पंक्ति में यदृच्छया लिखे जाते है तो दो के साथ आने की प्रायिकता है -
View Solutionएक त्रिभुज का एक शीर्ष (1,2) पर है तथा इससे होकर जाने वाली दो भुजाओं के मध्य - बिन्दु (−1,1) और (2,3) हैं , तो इस त्रिभुज का केन्द्रक है
View Solutionएक अतिपरवलय का केंद्र मूलबिंदु पर है तथा यह बिन्दु (4,2) से होकर जाता है और इसका अनुप्रस्थ (transverse) अक्ष X-अक्ष के अनुदिश है जिसकी लम्बाई 4 है तो इस अतिपरवलय की उत्केन्द्रता (eccentricity) है
View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
View Solutionयदि एक अतिपरवलय के संयुग्मी अक्ष की लम्बाई 5 है तथा इसकी नाभिको के बीच की दुरी 13 है, तो इस अतिपरवलय की उत्केंद्रता है
View Solutionमाना एक दीर्घवृत्त जिसका दीर्घ -अक्ष, X-अक्ष के अनुदिश है तथा केन्द्र मूलबिंदु पर है, के नाभिलम्ब की लम्बाई 8 है । यदि दीर्घवृत्त की नाभियो के बीच की दुरी, इसके लघु-अक्ष की लम्बाई के समान हो, तो निम्न में से कौन-सा बिन्दु इस पर स्थित है?
View Solutionयदि एक अतिपरवलय के शीर्ष (−2,0) तथा (2,0) पर है तथा इसकी एक नाभि (−3,0) पर है, तो निम्न में से कौन-सा बिन्दु इस अतिपरवलय पर स्थित नहीं है
View Solutionयदि एक वक्र बिंदु (1, -2) से होकर जाता है तथा इस पर किसी बिंदु (x, y) पर स्पर्श रेखा का ढाल (slope) x2−2yx है, तो यह वक्र निम्न में से किस बिंदु से होकर जाता है ?
View Solution