A force F=−K(yˆi+xˆj) (where K is a positive constant) acts on a particle moving in the x-y plane. Starting from the origin, the particle is taken along the positive x-axis to the point (a,0), and then parallel to the y-axis to the point (a,a). The total work done by the force F on the particle is
−2Ka2
2Ka2
−Ka2
Ka2
The correct Answer is:C
While moving from (0, 0) to (a, 0)
Along positive x-axis, y=0∴→F=−kxˆj
i.e., force is in negative y-direction while displacement is in positive x-direction.
∴W1=0
Because force is perpendicular to displacement
Then particle moves from (a, 0) to (a, a) along a line parallel to y-axis (x=+a) during this →F=−k(yˆi+aˆJ)
The first component of force, −kyˆi will not contribute any work because this component is along negative x-direction (−ˆi) while displacement is in positive y-direction (a, 0) to (a, a). The second component of force i.e., −kaˆj will perform negative work
∴W2=(−kaˆj)(aˆj)=(−ka)(a)=−ka2
So net work done on the particle W=W1+W2
=0+(−ka2)=−ka2
Topper's Solved these Questions
- WORK , ENERGY , POWER AND COLLISIONBook:ERRORLESS Chapter:WORK , ENERGY , POWER AND COLLISIONExercise:Graphical Questions
Explore 28 Videos
- WORK , ENERGY , POWER AND COLLISIONBook:ERRORLESS Chapter:WORK , ENERGY , POWER AND COLLISIONExercise:Assertion & Reason For AIIMS Aspirants
Explore 30 Videos
- WORK , ENERGY , POWER AND COLLISIONBook:ERRORLESS Chapter:WORK , ENERGY , POWER AND COLLISIONExercise:Ordinary Thinking (Objective Questions) (Perfectly Inelastic Collision)
Explore 30 Videos
- WAVES AND SOUNDBook:ERRORLESS Chapter:WAVES AND SOUNDExercise:SET
Explore 25 Videos
- WORK, ENERGY, POWER & COLLISIONBook:ERRORLESS Chapter:WORK, ENERGY, POWER & COLLISIONExercise:Assertion
Explore 30 Videos
Similar Questions
A force →F(yˆl+xˆJ), where K is a positive constant, acts on a particle moving in the XY-Plane. Starting from the origin, the particle is taken along the positive X-axis to a point (a,0) and then parallel to the y-axis to the point (a,a). Calculate the total work done by the force on the particle.
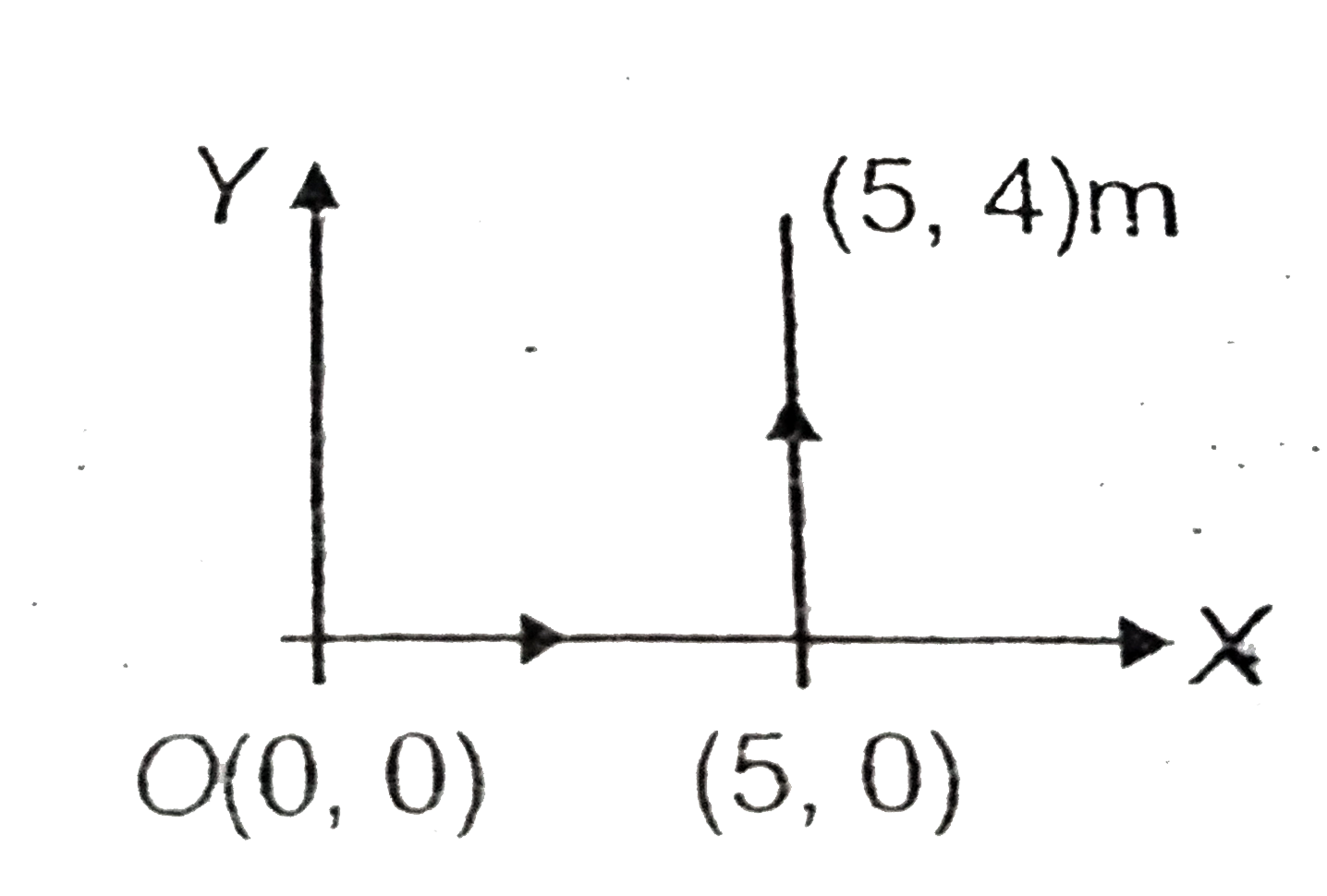
View SolutionA force →F=(4ˆi+5ˆj)N acts on a particle moving in XY plane. Starting from origin, the particle first goes along x-axis to the point (5.0) m and then parallel to the Y-axis to the point (5,4 m. The total work done by the force on the particle is
View Solution
Knowledge Check
A force F=−K(yˆi+xˆj) (where K is a positive constant) acts on a particle moving in the x-y plane. Starting from the origin, the particle is taken along the positive x-axis to the point (a,0), and then parallel to the y-axis to the point (a,a). The total work done by the force F on the particle is
A−2Ka2B2Ka2C−Ka2DKa2A force F=−K(yˆi+xˆj) (where K is a positive constant) acts on a particle moving in the x-y plane. Starting from the origin, the particle is taken along the positive x-axis to the point (a,0), and then parallel to the y-axis to the point (a,a). The total work done by the force F on the particle is
A−2Ka2B2Ka2C−Ka2DKa2A force F=−K(yˆi+xˆj), acts on a particle moving in the x-y plane. Starting from the origin, the particle is taken along the positive x-axis to the point (a,0) and then parallel to the y-axis to the point (a, a). The total work done by the force is
A−2Ka2B2Ka2C−Ka2DKa2
A single force acts on a particle situated on the negative x-axis. The torque about the origin is in the positive z-direction. The force is
View SolutionA force F acting on a particle varies with the position x as shown in figure. Find the work done by this force in displacing the particle from

View SolutionA force F=−K(yˆI+xˆj)(whereKisaposiveconstant)actsonapartic≤mov∈g∈thexypla≠.Start∈gformtheorig∈al,theparticalistakenalong∈thepositivexaξs→thep∮(x,0)andthenpartical→theyaξsthep∮(x,0).The→talworkdo≠bytheforceF on the particls is
View SolutionA force →F=k[yˆi+xˆj] where k is a positive constant acts on a particle moving in x-y plane starting from the point (3, 5), the particle is taken along a straight line to (5, 7). The work done by the force is :
View SolutionA force →F=(3→i+4→j)N, acts on a particle moving in x-y plane. Starting from origin, the particle first goes along x-axis to thepoint (4,0)m and then parallel to the y -axis to the point(4, 3)m. The total work done by the force on the particle is
(##NAR_NEET_PHY_XI_P2_C06_E09_014_Q01.png" width="80%">
View Solution

