A force →F=(3→i+4→j)N, acts on a particle moving in x-y plane. Starting from origin, the particle first goes along x-axis to thepoint (4,0)m and then parallel to the y -axis to the point(4, 3)m. The total work done by the force on the particle is
(##NAR_NEET_PHY_XI_P2_C06_E09_014_Q01.png" width="80%">
+12J
−6J
+24J
−12J
The correct Answer is:(3)
To solve the problem, we need to calculate the total work done by the force →F on the particle as it moves from the origin to the point (4, 3) m. The force is given as →F=3^i+4^j N.
1. Identify the Displacement Vector:
The particle moves from the origin (0, 0) to the point (4, 0) along the x-axis and then from (4, 0) to (4, 3) along the y-axis. The total displacement vector →S can be calculated as:
→S=(4−0)^i+(3−0)^j=4^i+3^j
2. Calculate the Work Done:
The work done W by a constant force is given by the dot product of the force vector →F and the displacement vector →S:
W=→F⋅→S
Substituting the values of →F and →S:
W=(3^i+4^j)⋅(4^i+3^j)
3. Calculate the Dot Product:
The dot product is calculated as follows:
W=(3⋅4)(^i⋅^i)+(4⋅3)(^j⋅^j)+(3⋅3)(^i⋅^j)+(4⋅4)(^j⋅^i)
Since ^i⋅^j=0 (the unit vectors are perpendicular), we have:
W=12+12+0+0=24 Joules
4. Conclusion:
The total work done by the force on the particle as it moves from the origin to the point (4, 3) m is:
W=24 Joules
The particle moves from the origin (0, 0) to the point (4, 0) along the x-axis and then from (4, 0) to (4, 3) along the y-axis. The total displacement vector →S can be calculated as:
→S=(4−0)^i+(3−0)^j=4^i+3^j
The work done W by a constant force is given by the dot product of the force vector →F and the displacement vector →S:
W=→F⋅→S
Substituting the values of →F and →S:
W=(3^i+4^j)⋅(4^i+3^j)
The dot product is calculated as follows:
W=(3⋅4)(^i⋅^i)+(4⋅3)(^j⋅^j)+(3⋅3)(^i⋅^j)+(4⋅4)(^j⋅^i)
Since ^i⋅^j=0 (the unit vectors are perpendicular), we have:
W=12+12+0+0=24 Joules
The total work done by the force on the particle as it moves from the origin to the point (4, 3) m is:
W=24 Joules
Topper's Solved these Questions
- WORK , ENERGY & POWER Book:NARAYNAChapter:WORK , ENERGY & POWER Exercise:EXERCISE -II (H.W)
Explore 75 Videos
- WORK , ENERGY & POWER Book:NARAYNAChapter:WORK , ENERGY & POWER Exercise:EXERCISE -III
Explore 54 Videos
- WORK , ENERGY & POWER Book:NARAYNAChapter:WORK , ENERGY & POWER Exercise:EXERCISE -1 (H.W)
Explore 60 Videos
- WAVESBook:NARAYNAChapter:WAVESExercise:Exercise-IV
Explore 56 Videos
- WORK POWER AND ENERGYBook:NARAYNAChapter:WORK POWER AND ENERGYExercise:Level-VI (Integer)
Explore 12 Videos
Similar Questions
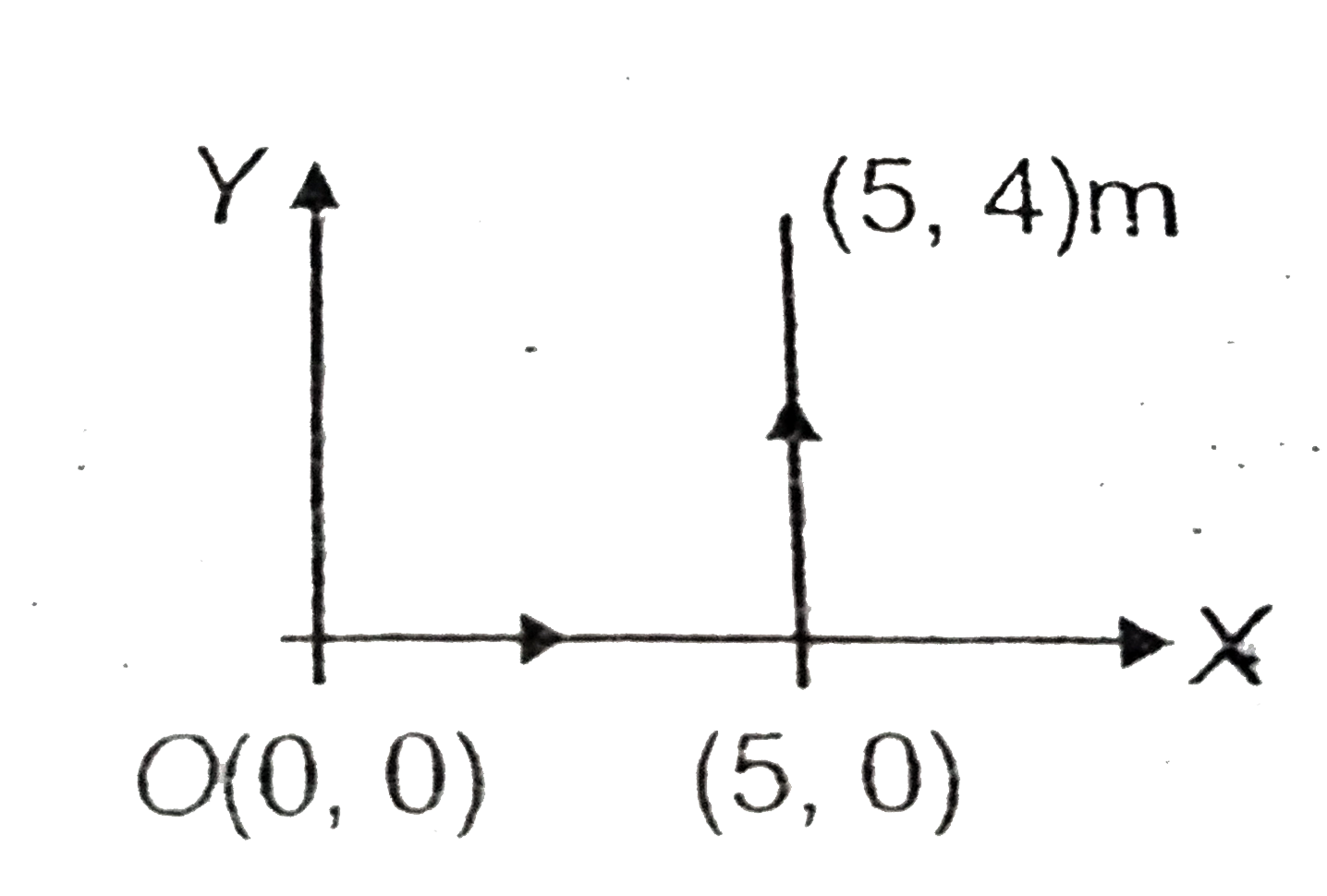
A force →F=(4ˆi+5ˆj)N acts on a particle moving in XY plane. Starting from origin, the particle first goes along x-axis to the point (5.0) m and then parallel to the Y-axis to the point (5,4 m. The total work done by the force on the particle is
View SolutionA force F=−k(^ˆi+xˆj) (where k is a positive constant) acts on a particle moving in the x−y plane. Starting from the origin, the particle is taken along the positive x-axis to the point (a,0) and then parallel to the y-axis to the point (a,a). The total work done by the force F on the particle is
(a) −2ka2 , (b) 2ka2,(c)-ka^(2),(d)ka^(2)
View Solution
Knowledge Check
A force F=−K(yˆi+xˆj), acts on a particle moving in the x-y plane. Starting from the origin, the particle is taken along the positive x-axis to the point (a,0) and then parallel to the y-axis to the point (a, a). The total work done by the force is
A−2Ka2B2Ka2C−Ka2DKa2A force F=−K(yˆi+xˆj) (where K is a positive constant) acts on a particle moving in the x-y plane. Starting from the origin, the particle is taken along the positive x-axis to the point (a,0), and then parallel to the y-axis to the point (a,a). The total work done by the force F on the particle is
A−2Ka2B2Ka2C−Ka2DKa2A force F=−K(yˆi+xˆj) (where K is a positive constant) acts on a particle moving in the x-y plane. Starting from the origin, the particle is taken along the positive x-axis to the point (a,0), and then parallel to the y-axis to the point (a,a). The total work done by the force F on the particle is
A−2Ka2B2Ka2C−Ka2DKa2
A force →F(yˆl+xˆJ), where K is a positive constant, acts on a particle moving in the XY-Plane. Starting from the origin, the particle is taken along the positive X-axis to a point (a,0) and then parallel to the y-axis to the point (a,a). Calculate the total work done by the force on the particle.
View SolutionA force F=−K(yˆI+xˆj)(whereKisaposiveconstant)actsonapartic≤mov∈g∈thexypla≠.Start∈gformtheorig∈al,theparticalistakenalong∈thepositivexaξs→thep∮(x,0)andthenpartical→theyaξsthep∮(x,0).The→talworkdo≠bytheforceF on the particls is
View SolutionA force F=−K(yˆi+xˆj) (where K is a positive constant) acts on a particle moving in the x-y plane. Starting from the origin, the particle is taken along the positive x-axis to the point (a,0), and then parallel to the y-axis to the point (a,a). The total work done by the force F on the particle is
View SolutionFour masses are fixed on a mass less rod as shown in Fig . The moment of inertia about the axis P is about :
(##NAR_NEET_PHY_XI_P2_C05_E06_024_Q01.png" width="80%">
View SolutionA force →F=(5→i+3→j+2→k)N is applied over a particle which displaces it from its origin to the point →r=(2→i−→j)m. The work done on the particle in joules is.
View Solution

