The volume of a gas and the number of gas molecules within that volume for four situations are
(1) 2V0andN0 (2) 3V0and3N0
(3) 8V0and4N0 (4) 3V0and9N0
Which of them has mean free path greatest?
1
2
3
4
The correct Answer is:A, C
To determine which situation has the greatest mean free path, we need to analyze the mean free path formula and the given conditions.
1. Understand the Mean Free Path Formula:
The mean free path (λ) can be expressed as:
λ=1√2πd2n
where:
- d is the diameter of the gas molecules (assumed constant for all cases),
- n is the number of molecules per unit volume.
2. Calculate the Number of Molecules per Unit Volume (n):
For each case, we will calculate n using the formula:
n=NV
where N is the number of molecules and V is the volume.
- Case 1: N=N0, V=2V0
n1=N02V0=12N0V0
- Case 2: N=3N0, V=3V0
n2=3N03V0=N0V0
- Case 3: N=4N0, V=8V0
n3=4N08V0=12N0V0
- Case 4: N=9N0, V=3V0
n4=9N03V0=3N0V0
3. Compare the Values of n:
- n1=12N0V0
- n2=N0V0
- n3=12N0V0
- n4=3N0V0
From this, we can see:
- Cases 1 and 3 have the smallest n values (12N0V0).
- Case 2 has a medium n value (N0V0).
- Case 4 has the largest n value (3N0V0).
4. Determine the Mean Free Path:
Since the mean free path is inversely proportional to n:
- The smaller the value of n, the larger the mean free path.
- Therefore, cases 1 and 3, which have the smallest n, will have the largest mean free path.
5. Conclusion:
The situations with the greatest mean free path are Case 1 and Case 3.
Final Answer:
The situations with the greatest mean free path are Case 1 and Case 3.
The mean free path (λ) can be expressed as:
λ=1√2πd2n
where:
- d is the diameter of the gas molecules (assumed constant for all cases),
- n is the number of molecules per unit volume.
For each case, we will calculate n using the formula:
n=NV
where N is the number of molecules and V is the volume.
n1=N02V0=12N0V0
n2=3N03V0=N0V0
n3=4N08V0=12N0V0
n4=9N03V0=3N0V0
- n1=12N0V0
- n2=N0V0
- n3=12N0V0
- n4=3N0V0
- Cases 1 and 3 have the smallest n values (12N0V0).
- Case 2 has a medium n value (N0V0).
- Case 4 has the largest n value (3N0V0).
Since the mean free path is inversely proportional to n:
- The smaller the value of n, the larger the mean free path.
- Therefore, cases 1 and 3, which have the smallest n, will have the largest mean free path.
The situations with the greatest mean free path are Case 1 and Case 3.
The situations with the greatest mean free path are Case 1 and Case 3.
Topper's Solved these Questions
- BOOK - MTG-WBJEECHAPTER - KINETIC THEORY OF GASES EXERCISE - WB JEE PREVIOUS YEARS QUESTIONS (MCQ)7videos
KINETIC THEORY OF GASES
- BOOK - MTG-WBJEECHAPTER - KINEMATICS EXERCISE - WB JEE Previous Years Questions (CATEGORY 3 : One or More than One Option Correct Type (2 Marks) )1videos
KINEMATICS
- BOOK - MTG-WBJEECHAPTER - LAWS OF MOTION EXERCISE - WB JEE PREVIOUS YEARS QUESTIONS (CATEGORY 3: ONE OR MORE THAN ONE OPTION CORRECT TYPE (2 MARKS))2videos
LAWS OF MOTION
Similar Questions
The volume of a given mass of gas at 273K is x ? The volume of it at 200C is V20 .Then its volume at 250C is
(1) 25x
(2) V20+(25x)/(273)
(3) V20+(5x)/(273)
(4) V20X5xView SolutionIn the following table the number of molecules N1 moving with definite velocity v1 m/s are given vi1.02.03.04.05.0Ni24682
.In the above question, the root mean square speed of particle is –View Solution
Knowledge Check
- Question 1 - Select One
For a gas sample with N0 number of molecules, function N (V) is given by : N(V)=dNdV=(2N0V30)V2 for 0<V<V0andN(V)=0 for V>V0. Where dN is number of molecules in speed range V to V + DV. The rms speed of the molecules is:
A√35V0B√25V0C√2V0D√3V0 - Question 2 - Select One
For a gas sample with N0 number of molecules, function N(V) is given by: N(V)=dNdV=(3N0V30)V2 for 0<V<V0 and N(V)=0 for V>V0. Where dN is number of molecules in speed range V to V+dV. The rms speed of the molecules is:
A√25V0B√35V0C√2V0D√3V0 - Question 3 - Select One
One mole of a mono- atomic ideal gas undergoes a quasi- static process, which is depicted by a straight line joining points (V0T0) and (2V0,3T0) in a V - T diagram . What is the value of the heat capacity of the gas at the point (V0,T0) ?
ARB32RC2RD0
In the following table the number of molecules N1 moving with definite velocity v1 m/s are given vi1.02.03.04.05.0Ni24682
. The mean speed of particle is –View SolutionGiven the set of vectors v1=(1,2,3):v2=(1,0,1) and v3=(0,1,0)
View SolutionFor a gas sample with N0 number of molecules, function N(v) is given by : N(v)=dNdv=(3N0v30)v2 for 0<v<v0andN(v)=0 for v>v0, where dN is number of molecules in speed range v to v+dv. Find the rms speed of the molecules.
View SolutionA monoatomic gas expands following as thermodynamic law P=C1V+C2, where C1,C2 are constants, from state A(V0,3P0) to B(3V0,P0).What will be the volume of the gas upto which it absorbs heat?
View Solutionn moles of gas in a cylinder under a piston is transferred infinintley slowly from a state with a volume of V0 and a pressure 3P0 to a state with a volume of 3V0 and a pressure P0 as shown in Fig. The maximum temperature that gas will reach in this process is
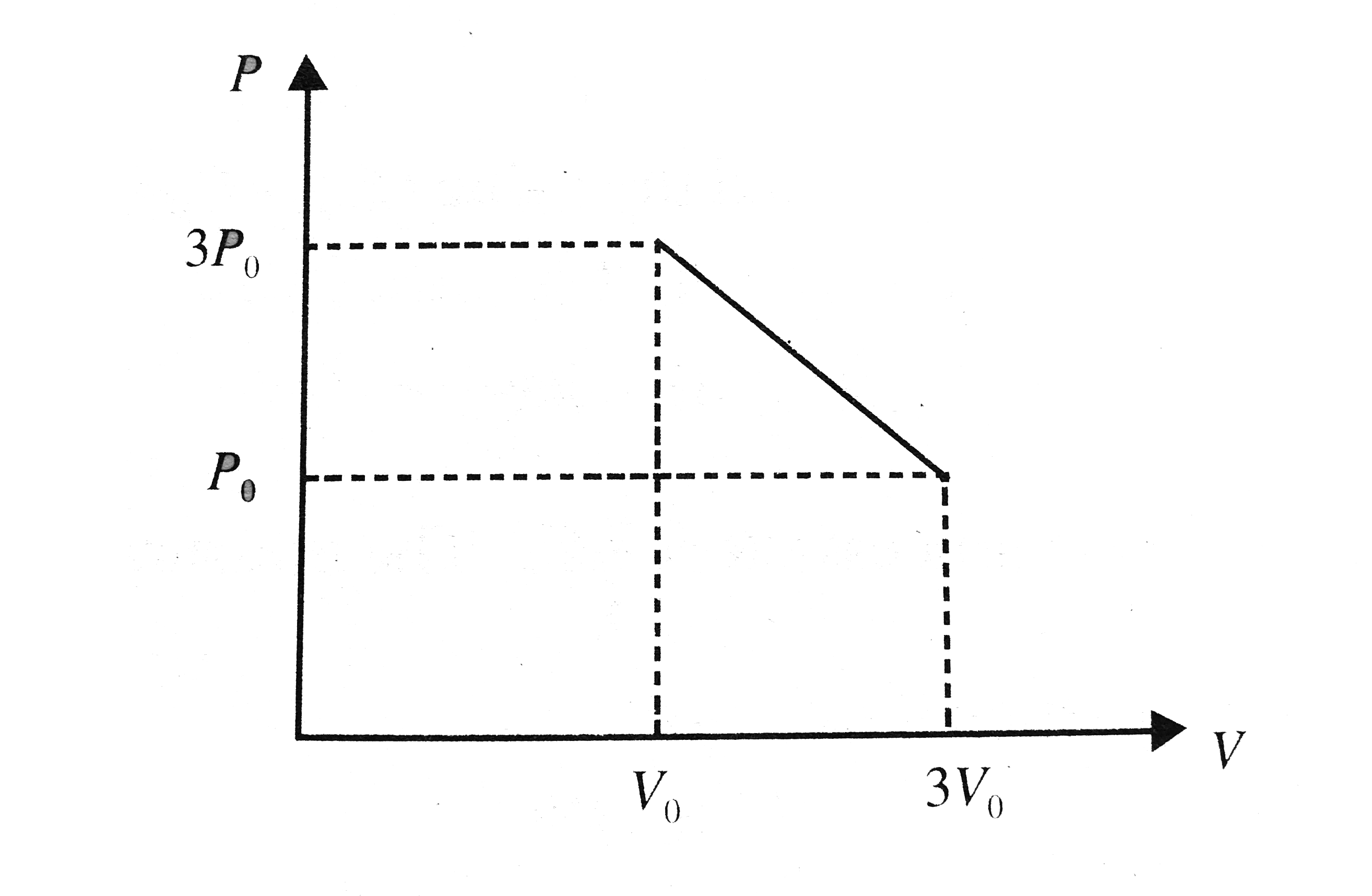 View Solution
View Solution
