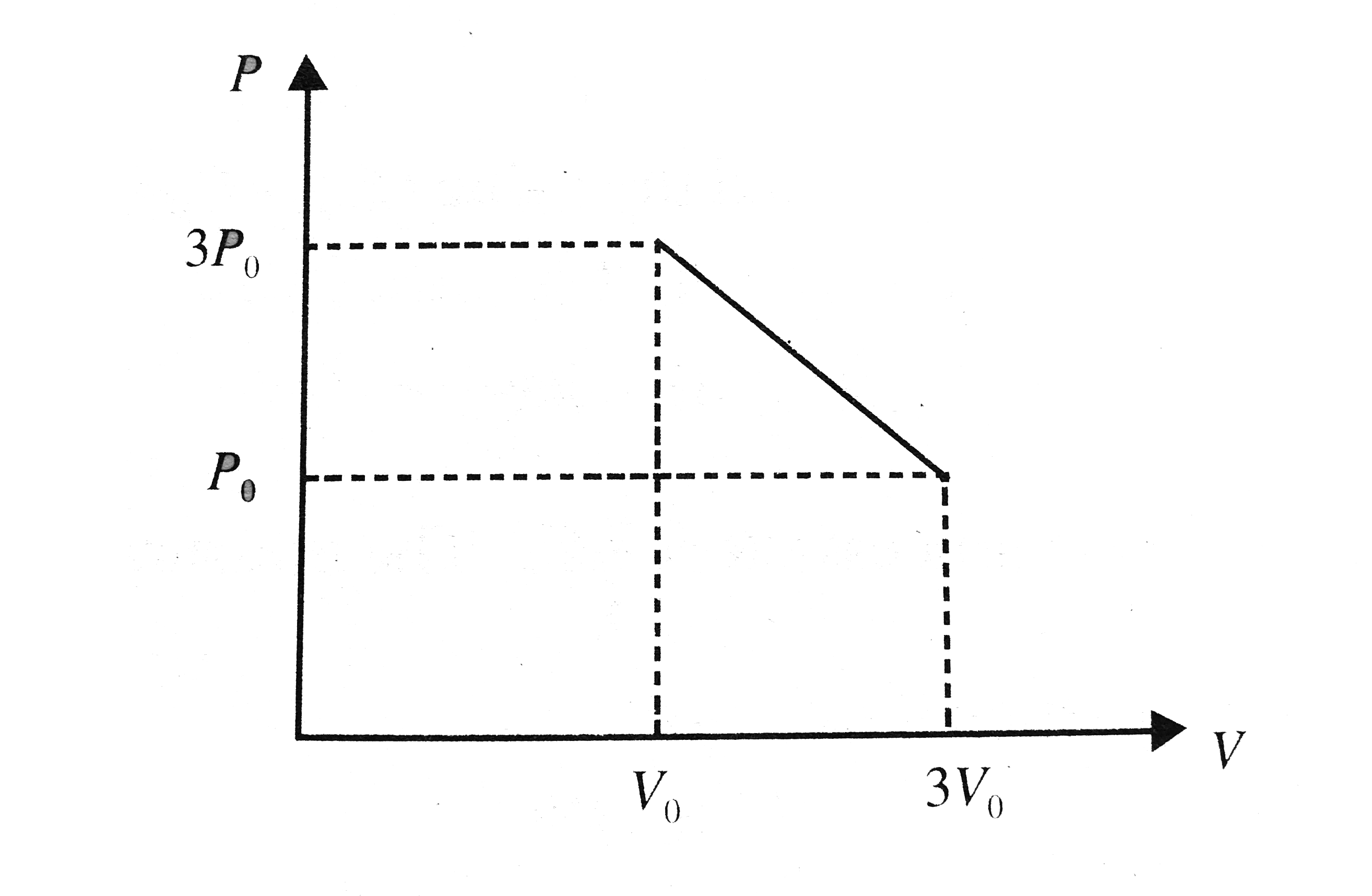
n moles of gas in a cylinder under a piston is transferred infinintley slowly from a state with a volume of V0 and a pressure 3P0 to a state with a volume of 3V0 and a pressure P0 as shown in Fig. The maximum temperature that gas will reach in this process is
P0V0nR
3P0V0nR
4P0V0nR
2P0V0nR
The correct Answer is:C
c. P−P1P1−P2=V−V2V1−V2
(P−P1)(V1−V2)=(V1−V2)=(V−V1)(P1−P2)
(P−3P0)(V0−3V0)=(V−V0)(3P0−P0)
(P−3P0)(−2V0)=(V−V0)(2P0)
−2V0P+6P0V0=2VP0−2P0V0
2VP0+2V0P−8P0V0=0
VP0+V0nRTV−4P0V0=0
V2P0−4P0V0+V0nRT=0
T=P0(V2+4VV0)V0nR
For maximum of minimum value of T,
dTdV=−2V+4V0=0⇒V=2V0
d2TdV2=−2
It is negative so T is maximum at
V=2V0
Tmax=P0(−V20+8V20)V0nR=4P0V0nR
Topper's Solved these Questions
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Multiple Corrects
29 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Assertion-Reasoning
6 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Subjective
22 Videos
- KINETIC THEORY OF GASESBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression
2 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Multiple Correct Answer Type
9 Videos
Similar Questions
20 g of helium ( M = 4) in a cylinder under a piston are transferred infinitely slowly form a state of volume V1=0.032m2 and pressure p1=4.1 atm to a state of volume V2=0.009m3 and p2=15.5 atm. What maximum temperature will the gas reach if the prssure decrease linearly with volume ?
View SolutionIf a gas of a volume V1 at pressure p1 is compressed adiabatically to volume V2 and pressure p2, calculate the work done by the gas.
View Solution
Knowledge Check
If n moles of an ideal gas are expanded is isothermally and reversibly from an initial state in which it has pressure p1 and volume V1 to the final state of volume V2 and pressure P2, then
AΔSsys=−2.303nRlog(P1p2)BΔSsys=2.303Rnlog(P1p2)CΔSsys=−2.303Rnlog(P1p2)DΔSsys=2.303nRlog(P1p2)One mole of an ideal monotomic gas undergoes a linear process from A to B in which its pressure p and its volume V change as shown in figure.

The maximum temperature of the gas during this process isAp0V02RBp0V04RC3p0V04RD3p0V02RIf a gas of a volume V1 at pressure p1 is compressed adiabatically to volume V2 and pressure p2, calculate the work done by the gas.
AzeroBnegativeCpositiveDMay be negative or positive
Draw the P-T and V-T diagrams of an isochoric process of n moles an ideal gas from pressure P0 volume V0 to pressure 4P0, indicating the pressures and temperatures of the gas in the initial and the final states.
View Solutionn' moles of an ideal gas undergoes a process A→B as shown in the figure. The maximum temperature of the gas during the process will is p0v04nR then value of N is:
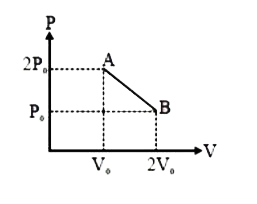
View SolutionThermal coefficient of volume expansion at constant pressure for an ideal gas sample of n moles having pressure P0, volume V0, and temperature T0 is
View SolutionOne mole of an ideal monotomic gas undergoes a linear process from A to B in which its pressure p and its volume V change as shown in figure.
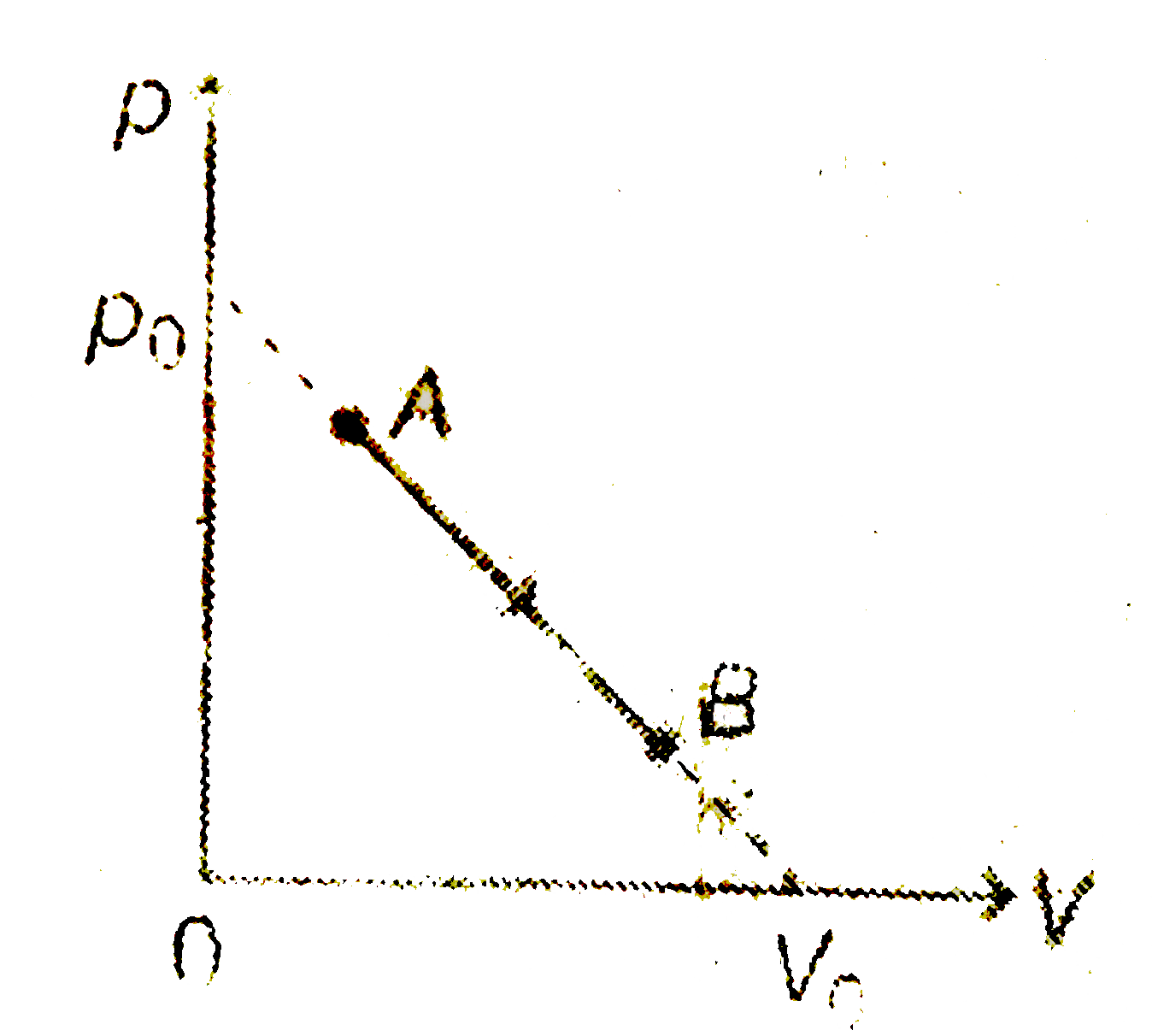
The absolute temperature T versus volume V for the given process is
View SolutionOne mole of an ideal monatomic gas undergoes a linear process from A to B , in which is pressure P and its volume V change as shown in figure .
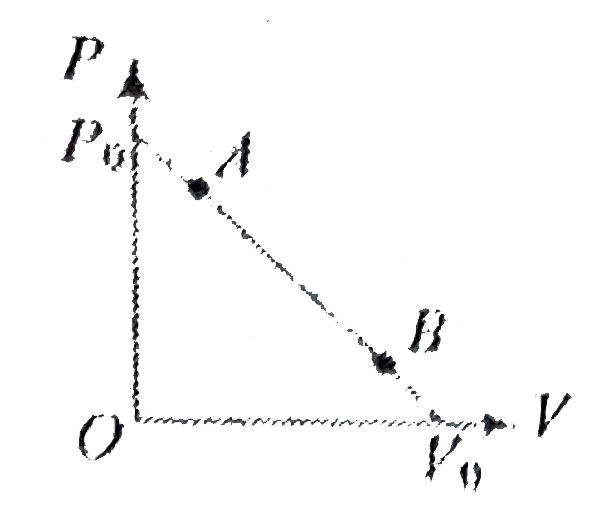
The absolute temperature T versus volume V for the given process is
View Solution
