The ratio of pressure of the same gas in two containers in where & are the number of moles and & are respective temperatures. If the containers are now joined find the ratio of pressure to the pressure :
none of these
The correct Answer is:A
a. Given
. It implies that volume of both containers is same. After mixing.
Topper's Solved these Questions
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBook:CENGAGE PHYSICSChapter:KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSExercise:Multiple Corrects
Explore 29 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBook:CENGAGE PHYSICSChapter:KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSExercise:Assertion-Reasoning
Explore 6 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBook:CENGAGE PHYSICSChapter:KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSExercise:Subjective
Explore 22 Videos
- KINETIC THEORY OF GASESBook:CENGAGE PHYSICSChapter:KINETIC THEORY OF GASESExercise:Compression
Explore 2 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICSChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Multiple Correct Answer Type
Explore 9 Videos
Similar Questions
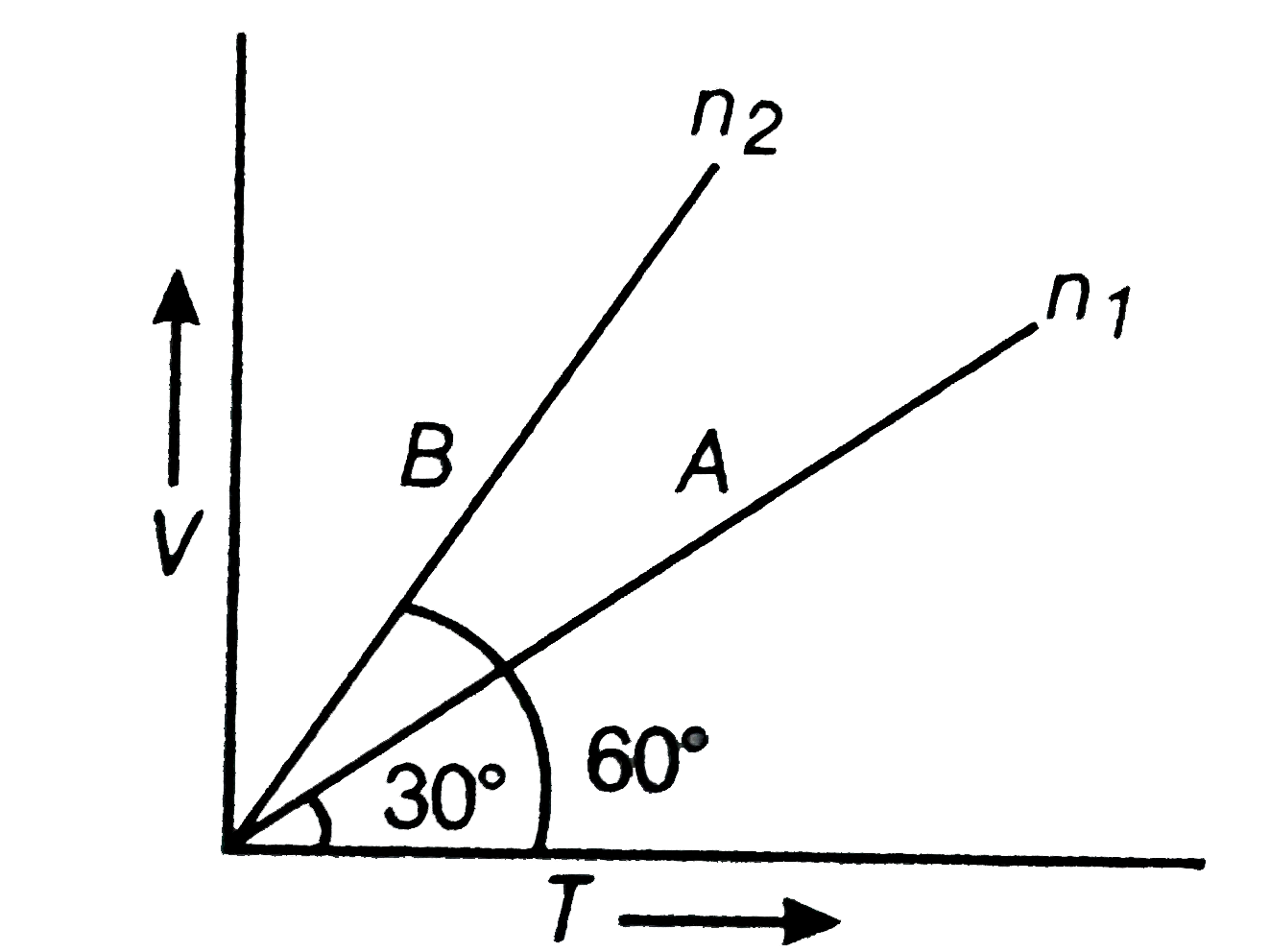
Two gases A and B at same pressure contain number of moles n1andn2. Their volume temperature graphs are shown in figure. Then the ratio
View SolutionTwo ideal polyatomic gases at temperature T1 and T2 are mixed so that there is no loss of energy . If F1 and F2,m1 and m2,n1 and n2 be the degrees of freedom, masses, number of molecules of the firest and second gas respectively, the temperature of mixture of these two gases is :
View Solution
Knowledge Check
Three containes of the same volume contain three different gases. The masses of the molecules are m1,m2 and m3 and the number of molecules in their respective containers are N1,N2 and N3. The gas pressure in the containers are P1,P2 and P3 respectively. All the gases are now mixed and put in one of the containers. The pressure P of mixture will be
AP<(P1+P2+P3)BP=P1+P2+P33CP=P1+P2+P3DP>(P1+P2+P3)Three perfect gases at absolute temperature T1,T2 and T3 are mixed. The masses f molecules are m1,m2 and m3 and the number of molecules are n1,n2 and n3 respectively. Assuming no loss of energy, the final temperature of the mixture is
A(T1+T2+T3)3Bn1T1+n2T2+n3T3n1+n2+n3Cn1T21+n2T22+n3T23n1T1+n2T2+n3T3Dn21T21+n22T22+n23T23n1T1+n2T2+n3T3n1 and n2 moles of two ideal gases (mo1 wt m1 and m2) respectively at temperature T1K and T2K are mixed Assuming that no loss of energy the temperature of mixture becomes .
An1T1+n2T2Bn1T1+n2T2T1+T2Cn2T1+n1T2n1+n2DT1×T2n1×n2
A thick spherical shell of inner and outer radii r and R respectively has thermal conductivity k=ρxn , where ρ is a constant and x is distance from the centre of the shell. The inner and outer walls are maintained at temperature T1 and T2(<T1)
(a) Find the value of number n (call it n0) for which the temperature gradient remains constant throughout the thickness of the shell.
(b) For n=n0, find the value of x at which the temperature is T1+T22
(c) For n=n0, calculate the rate of flow of heat through the shell.
View SolutionAir contains N2 and O2 in the ratio of 4:1 by volume. The average conditions of temperature and pressure ?
View SolutionTwo containers of equal volume contain the same gas at pressure P1 and P2 and absolute temperature T1 and T2, respectively. On joining the vessels, the gas reaches a common pressure P and common temperature T. The ratio P/T is equal to
View SolutionTwo perfect gases at absolute temperature T1andT2 are mixed. There is no loss of energy. The masses of the molecules are m1andm2. The number of molecules in the gases are n1andn2. The temperature of the mixture is
View SolutionTwo adiabatic containers have volumes V1 and V2 respectively. The first container has monoatomic gas at pressure p1 and temperature T1. The second container has another monoatomic gas at pressure p2 and temperature T2. When the two containers are connected by a narrow tube, the final temperature and pressure of the gases in the containers are P and T respectively. Then
View Solution

