The area of the region bounded by the parabola y=x2+1 and the line x+y=3 is ………..sq. units .Solution in Gujrati
457
254
π18
92
The correct Answer is:D
Step by step video, text & image solution for The area of the region bounded by the parabola y= x^2 +1 and the line x+y =3 is ………..sq. units . by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- APPLICATION OF INTEGRALSBook:KUMAR PRAKASHANChapter:APPLICATION OF INTEGRALSExercise:PRACTICE PAPER ( SECTION -A)
Explore 6 Videos
- APPLICATION OF INTEGRALSBook:KUMAR PRAKASHANChapter:APPLICATION OF INTEGRALSExercise:PRACTICE PAPER ( SECTION -B)
Explore 3 Videos
- APPLICATION OF INTEGRALSBook:KUMAR PRAKASHANChapter:APPLICATION OF INTEGRALSExercise:SOLUTIONS OF NCERT EXAMPLAR PROBLEMS ( OBJECTIVE TYPE QUESTIONS)
Explore 11 Videos
- APPLICATION OF DERIVATIVES Book:KUMAR PRAKASHANChapter:APPLICATION OF DERIVATIVES Exercise:PRACTICE PAPER - 6 (SECTION - D)
Explore 2 Videos
- BOARD'S QUESTION PAPER MARCH - 2020Book:KUMAR PRAKASHANChapter:BOARD'S QUESTION PAPER MARCH - 2020Exercise:PART - B (Section - C)
Explore 4 Videos
Similar Questions
The area of the region bounded by the curve y=2x−x2 and X -axis is ….. Sq . Units .
View SolutionUsing integration , find the ara of the region bounded by the circle x2+y2=a2
View SolutionThe area bounded by the Y-axis ,y=cosxandy=sinx when 0≤x≤π2 is
View SolutionIf the length of three sides of a trapezium other than base are equal to 10 cm. Than find the area of trapezium when it is maximum.
View SolutionFind the global maximum and minimum values of the function f given by f(x)=2x3−15x2+36x+1,x∈[1,5].
View SolutionThe area (in sq units) of the region bounded by the curve y=sqrt(x) and the lines y=0,y=x-2, is
View SolutionThe area (in sq. units) of the region bounded by the parabola y=x2+2 and the lines y=x+1,x=0 and x=3, is
View SolutionThe area (in sq units) of the region bounded by the parabola, y=x2+2 and the lines, y=x+1,x=0andx=3, is
View SolutionThe area of the region (in sq units), in the first quadrant, bounded by the parabola y=9x2 and the lines x = 0, y = 1 and y = 4, is
View SolutionThe area of the plane region bounded by the curve x=y2−2 and the line y = - x is (in sq units)
View SolutionThe area (in sq. units) of the region bounded by x=−1,x=2,y=x2+1andy=2x−2 is
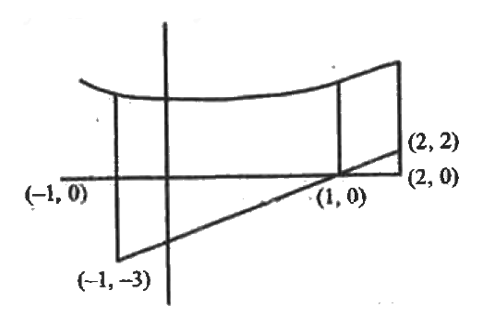
View SolutionThe area of the region bounded by the curves y=x3,y=1x,x=2 and x - axis (in sq. units) is
View SolutionThe area of the region (in sq. units), in the first quadrant, bounded by the parabola y=9x2 and the lines x=0,y=1andy=4 is
View SolutionThe area (in sq. units) of the region bounded by the parabola y=x2+2 and the lines y=x+1,x=0 and x=3, is
View SolutionThe area of the region bounded by the lines y=mx,x=1,x=2, and x axis is 6 sq, units, then 'm' is
View Solution
