A gas follow P=kV3.Find work done in raising temperature from 100oC to 300oC
To solve the problem of finding the work done in raising the temperature of a gas that follows the relationship P=kV3 from 100∘C to 300∘C, we will follow these steps:
Step 1: Understand the relationship between pressure, volume, and work done
The work done W by a gas during expansion or compression can be expressed as:
W=∫V2V1PdV
Given that P=kV3, we can substitute this into the equation for work done.
Step 2: Substitute the expression for pressure into the work integral
Now substituting P into the work integral, we have:
W=∫V2V1kV3dV
Step 3: Perform the integration
Since k is a constant, we can take it out of the integral:
W=k∫V2V1V3dV
The integral of V3 is:
∫V3dV=V44
Thus, we can evaluate the definite integral:
W=k(V44)V2V1=k(V424−V414)=k4(V42−V41)
Step 4: Relate pressure, volume, and temperature using the ideal gas law
Using the ideal gas law PV=nRT, we can express kV4 in terms of pressure and temperature:
P1V1=nRT1andP2V2=nRT2
Thus, we can write:
kV41=P1V1andkV42=P2V2
Substituting these into our expression for work:
W=14(P2V2−P1V1)
Step 5: Substitute the expressions for pressure and temperature
From the ideal gas law:
W=14(nRT2−nRT1)
Factoring out nR:
W=nR4(T2−T1)
Step 6: Convert temperatures to Kelvin and calculate the difference
Convert the temperatures from Celsius to Kelvin:
T1=100∘C=373KandT2=300∘C=573K
The difference in temperature is:
T2−T1=573−373=200K
Step 7: Final expression for work done
Substituting the temperature difference back into the work equation:
W=nR4×200
Thus, the work done in raising the temperature from 100∘C to 300∘C is:
W=50nR
The work done W by a gas during expansion or compression can be expressed as:
W=∫V2V1PdV
Given that P=kV3, we can substitute this into the equation for work done.
Now substituting P into the work integral, we have:
W=∫V2V1kV3dV
Since k is a constant, we can take it out of the integral:
W=k∫V2V1V3dV
The integral of V3 is:
∫V3dV=V44
Thus, we can evaluate the definite integral:
W=k(V44)V2V1=k(V424−V414)=k4(V42−V41)
Using the ideal gas law PV=nRT, we can express kV4 in terms of pressure and temperature:
P1V1=nRT1andP2V2=nRT2
Thus, we can write:
kV41=P1V1andkV42=P2V2
Substituting these into our expression for work:
W=14(P2V2−P1V1)
From the ideal gas law:
W=14(nRT2−nRT1)
Factoring out nR:
W=nR4(T2−T1)
Convert the temperatures from Celsius to Kelvin:
T1=100∘C=373KandT2=300∘C=573K
The difference in temperature is:
T2−T1=573−373=200K
Substituting the temperature difference back into the work equation:
W=nR4×200
Thus, the work done in raising the temperature from 100∘C to 300∘C is:
W=50nR
Topper's Solved these Questions
- JEE MAIN 2021Book:JEE MAINS PREVIOUS YEARChapter:JEE MAIN 2021Exercise:SECTION-A
Explore 80 Videos
- JEE MAIN 2021Book:JEE MAINS PREVIOUS YEARChapter:JEE MAIN 2021Exercise:SECTION-B
Explore 40 Videos
- JEE MAINBook:JEE MAINS PREVIOUS YEARChapter:JEE MAINExercise:All Questions
Explore 473 Videos
- JEE MAIN 2022Book:JEE MAINS PREVIOUS YEARChapter:JEE MAIN 2022Exercise:Question
Explore 492 Videos
Similar Questions
In a certain thermodynamical process, the pressure of a gas depends on its volume as kV3. The work done when the temperature changes from 100∘C to 300∘C will be x times nR, where n denotes number of moles of a gas. Find x.
View SolutionPressure p, volume V and temperature T for a certain gas are related by
p=αT−βT2V
where, α and β are constants. Find the work done by the gas if the temperature changes from T1 to T2 while the pressure remains the constant.
View Solution
Knowledge Check
Find the work done by the gas in the process ABC.
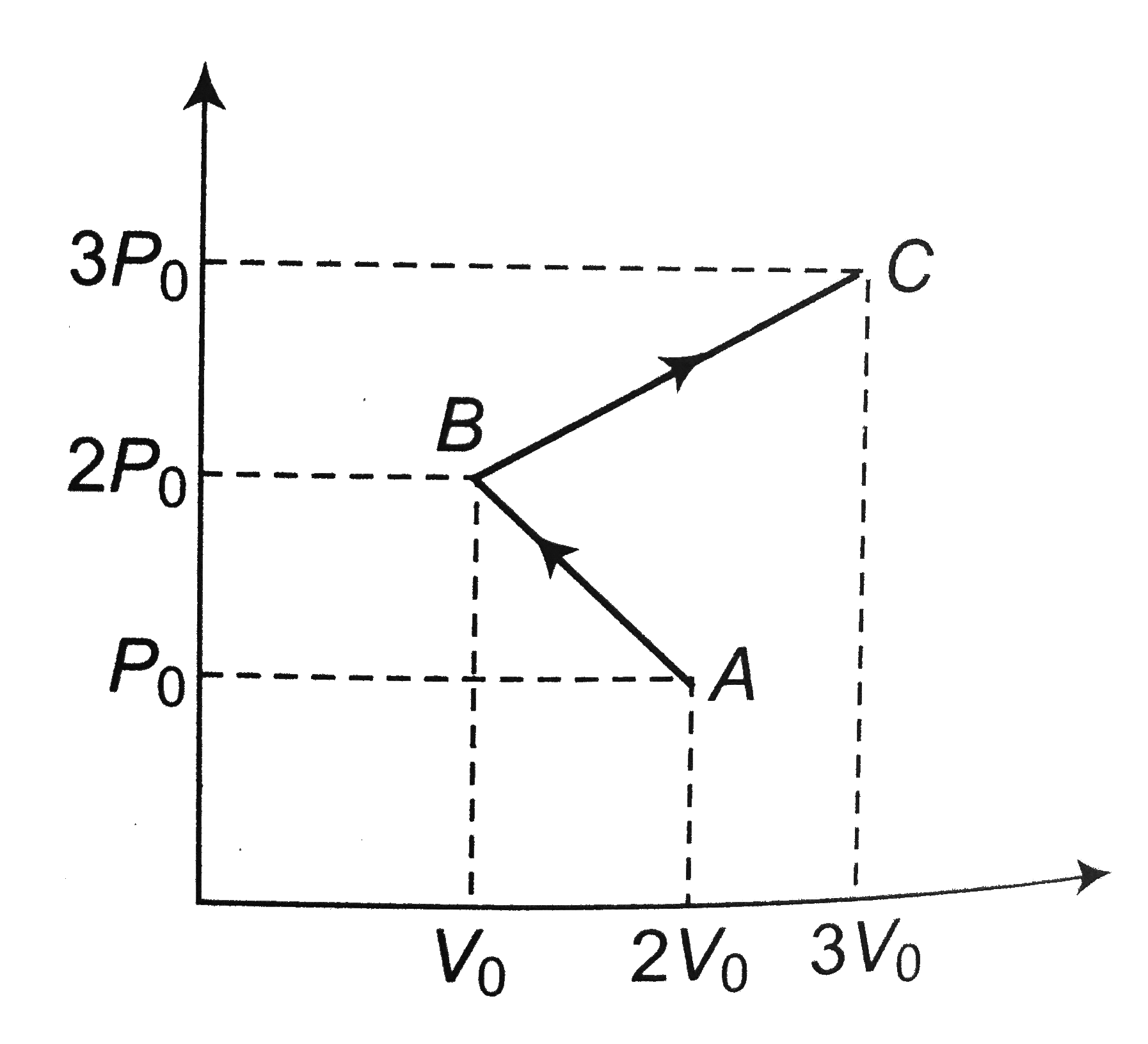 A32P0V0B52P0V0C72P0V0D4P0V0
A32P0V0B52P0V0C72P0V0D4P0V0n moles of an ideal gas undergo a process in which the temperature changes with volume as T=kv2. The work done by the gas as the temperature changes from 70 to 470 is
A3nRT0B(52)nRT0C(32)nRT0DZeroFind work done by the gas in the process shown in figure.
 A52πatmLB52atmLC−32πatmLD−54πatmL
A52πatmLB52atmLC−32πatmLD−54πatmL
Two moles of a monoatomic gas at 300K are kept in a non conducting container enclosed by a piston . Gas is now compressed to increase the temperature from 300K to 400K. Find work done by the gaS (R=253J/mol−K)
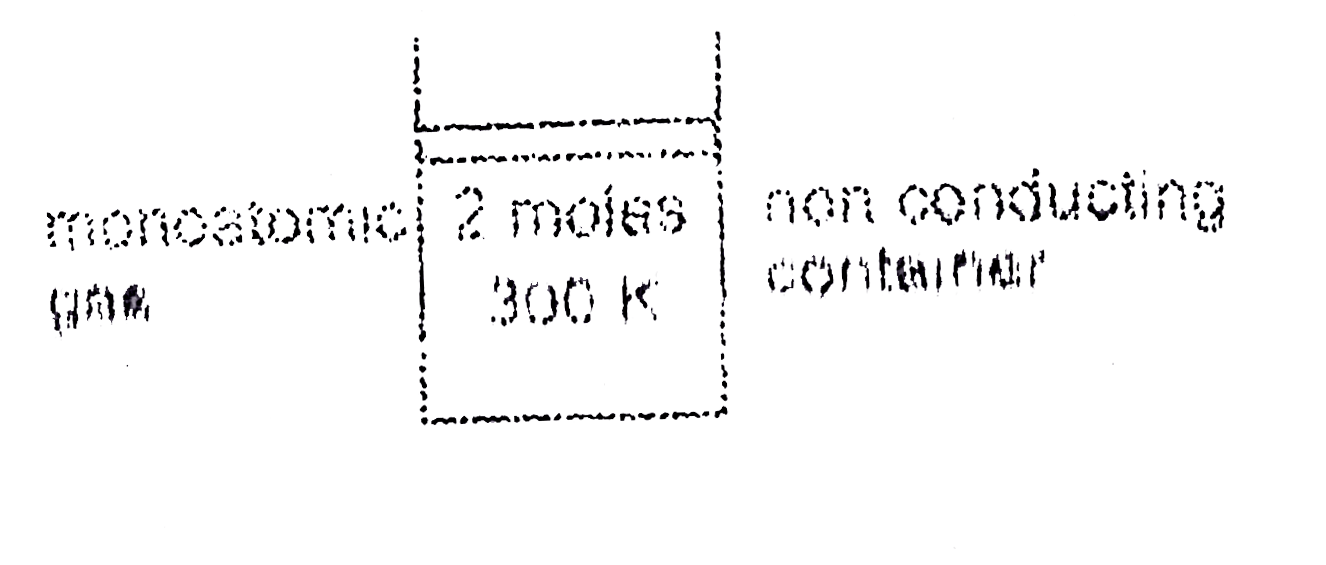
View SolutionTwo moles of a diatomic gas at 300 K are kept in a nonconducting container enclosed by a piston . Gas is now compressed to increase the temperature from 300 K to 400 K. Find word done by the gas

View SolutionAn ideal gas is enclosed in a cyclinder with a movable piston on top. The piston has mass of 8000g and an area of 5.00cm2 and is free to slide up and down, keeping the pressure of the gas constant. How much work is done as the temperature of 0.200mol of the gas is raised from 200∘C to 300∘C?
View Solution
In the adjoining diagram, the p-V graph of an ideal gas is shown. Find out from the graph (i) work done in taking the gas
From the state A→B (ii) Work done in taking the gas from B→C (iii) Work done in a complete cycle. (1 litre=10−3m3)
View SolutionFind work done by the gas in the process shown in figure :
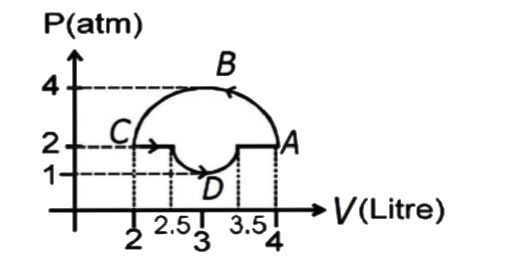
View Solution