माना A(3, 2) तथा B(5, 1) है। भुजा AB पर मूल बिन्दु से दूर समबाहु त्रिभुज ABP बनाया जाता है, तो त्रिभुज ABP का लम्ब केन्द्र है-
(4−12√3,32−√3)
(4+12√3,32+√3)
(4−16√3,32−12√3)
(4+16√3,32+13√3)
The correct Answer is:D
Step by step video, text & image solution for माना A(3, 2) तथा B(5, 1) है। भुजा AB पर मूल बिन्दु से दूर समबाहु त्रिभुज ABP बनाया जाता है, तो त्रिभुज ABP का लम्ब केन्द्र है- by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- बिन्द् एवं सरल रेखा Book:ALLEN HINDIChapter:बिन्द् एवं सरल रेखा Exercise:EXERCISE-03 (MISCELLANEOUS TYPE QUESTIONS) (स्तम्भ सुमेलन (Match the column)
Explore 2 Videos
- बिन्द् एवं सरल रेखा Book:ALLEN HINDIChapter:बिन्द् एवं सरल रेखा Exercise:EXERCISE-03 (MISCELLANEOUS TYPE QUESTIONS) (कथन एवं कारण (Assertion & Reason))
Explore 4 Videos
- बिन्द् एवं सरल रेखा Book:ALLEN HINDIChapter:बिन्द् एवं सरल रेखा Exercise:EXERCISE-01 (CHECK YOUR GRASP) ( सही विकल्पों को चुनिए (एक या एक से अधिक सही उत्तर हैं))
Explore 7 Videos
- द्विपद प्रमेयBook:ALLEN HINDIChapter:द्विपद प्रमेयExercise:Exercise -04 [B]
Explore 10 Videos
- लघुगणक Book:ALLEN HINDIChapter:लघुगणक Exercise:DO YOURSELF -6
Explore 2 Videos
Similar Questions
निम्न प्रश्नों में दो स्तम्भ में वक्तव्य (statements) दिये हुए हैं जिनका सुमे (match) करना है।स्तम्भ-I (Column-I) के वक्तव्यों को A,B,C तथा D नामित किया गया है जबकिस्तम्भ-II (Column-II) के वक्तव्यों को p,q,r तथा नामित किया गया है।स्तम्भ-I(Column-I) में दिए गए कोई एक वक्तव्यस्तम्भ-II (Columm-II) के एक वक्तव्य से सही सुमेल करता है।
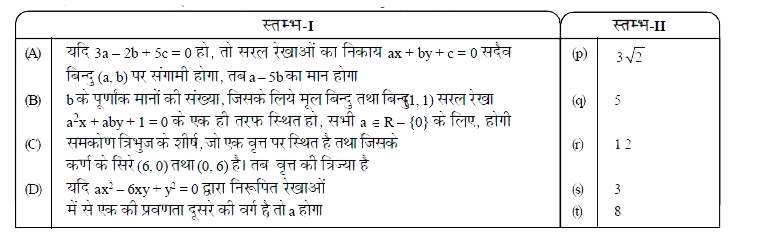
View Solutionमाना L1:a1x+b1y+c1=0,L2:a2x+b2y+c2=0 तथा L3:a3x+b3y+c3=0 है।
कथन-I :L1:L2:L3 तीन सर्वांगसम रेखायें है, तो ∣∣ ∣∣a1b1c1a2b2c2a3b3c3∣∣ ∣∣=0 होगा। क्योंकि
कथन-II : यदि ∣∣ ∣∣a1b1c1a2b2c2a3b3c3∣∣ ∣∣=0 हो, तो रेखायें L1,L2 तथा L3 संगामी होगी।
View Solutionरेखा 2x +3y+7= 0 पर स्थित बिन्दु के निर्देशांक जो बिन्दु (1,-3) से 3 इकाई दूरी पर हो-
View Solutionयदि 2n∑r=0ar(x−2)r=2n∑r=0br(x−3)r और सभी k≥n के लिए ak=1 तो दिखाइए की bn=2n+1Cn+1
View Solutionहल कीजिए :|x+3|=2(5−x)
View Solutionसिद्ध कीजिये की बिंदु (a,a),(-a,-a),(-a√3,a√3) एक समबाहु त्रिभुज के निर्देशांक है
View Solutionकिसी समबाहु त्रिभुज के आधार का समीकरण x+y=2 है तथा सामने के शीर्ष के निर्देशांक (2,1) है , त्रिभुज की शेष भुजाओ के समीकरण ज्ञात कीजिए ।
View Solutionमाना A(2,−3) तथा B(−2,1) एक त्रिभुज ABC के शीर्ष है । यदि इस त्रिभुज का केन्द्रक सरल रेखा 2x+3y=1पर भ्रमण करता है तो शीर्ष C का बिन्दुपथ है -
View Solutionसरल रेखाओं 4x−7y+10=0,x+y=5 व 7x+4y=15 द्वारा बने त्रिभुज का लम्ब केन्द्र है:
View Solutionमान A(2,−3) तथा B(−2,1) एक त्रिभुज ABC के शीर्ष है। यदि इस त्रिभुज का केन्द्रक सरल रेखा 2x+3y=1 पर भ्रमण करता है, तो शीर्ष C का बिन्दुपथ है:
View Solutionयदि O मूल बिन्दु तथा A(a,b,c) है तो A से जाने वाले एवं OA लम्ब समतल का समीकरण है -
View Solutionउस समतल का सदिश समीकरण जो बिन्दु A(4,7,−4) से जाता है तथा सदिश (3,2,−1)पर लम्ब है -
View Solutionयदि →a,→b तथा →c समबाहु त्रिभुज के शीर्ष के स्थिति सदिश हो जिसका लम्ब केंद्र मूलबिंदु है , तो →a+→b+→c का मान ज्ञात कीजिए।
View Solutionमाना एक ऊर्ध्वाधर मीनार AB ऐसी है कि उसका सिरा A भूमि पर है। माना AB का मध्य-बिन्दु C है और भूमि पर स्थित बिन्दु P ऐसा है कि AP=2AB यदि ∠BPC=β है, तो tanβ बराबर है
View Solutionएक अतिपरवलय बिन्दु P(√2,√3) से होकर जाता है, तथा उसकी नाभियाँ (±2,0) पर है, तो अतिपरवलय के बिन्दु P पर खींची गई स्पर्श रेखा जिस बिन्दु से होकर जाती है, वह है
View Solutionएक त्रिभुज का एक शीर्ष (1,2) पर है तथा इससे होकर जाने वाली दो भुजाओं के मध्य - बिन्दु (−1,1) और (2,3) हैं , तो इस त्रिभुज का केन्द्रक है
View Solution

