Passage - I:
A rod of length 2m is at a temperature of 20∘C. Find the free expansion of the rod, if the temperature is increased to 50°C, then find stress produced when the rod is
Permitted to expand by 0.4 mm. Y=2×1011N/m2,α=15×10−6/∘CSolution in Telugu
7×107N/m2
5×107N/m2
7×108N/m2
5×108N/m2
The correct Answer is:B
Step by step video, text & image solution for Passage - I: A rod of length 2m is at a temperature of 20^(@) C. Find the free expansion of the rod, if the temperature is increased to 50°C, then find stress produced when the rod is Permitted to expand by 0.4 mm. Y= 2 xx 10^( 11) N//m^(2) , alpha = 15 xx 10^(-6) //^(@) C by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- THERMAL PROPERTIES OF MATTERBook:AAKASH SERIESChapter:THERMAL PROPERTIES OF MATTERExercise:EXPANSION OF SOLIDS (LECTURE SHEET) Matrix Matching Type Questions
Explore 2 Videos
- THERMAL PROPERTIES OF MATTERBook:AAKASH SERIESChapter:THERMAL PROPERTIES OF MATTERExercise:EXPANSION OF SOLIDS (LECTURE SHEET) Integer Type Questions
Explore 5 Videos
- THERMAL PROPERTIES OF MATTERBook:AAKASH SERIESChapter:THERMAL PROPERTIES OF MATTERExercise:EXPANSION OF SOLIDS (LECTURE SHEET) Straight Objective Type Questions
Explore 14 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBook:AAKASH SERIESChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTIONExercise:PRACTICE EXERCISE
Explore 99 Videos
- THERMODYNAMICSBook:AAKASH SERIESChapter:THERMODYNAMICSExercise:EXERCISE - 3
Explore 33 Videos
Similar Questions
Column-IColumn-IlA) Thermal stress,P)3αΔt(100)B) Loss in time of a pendulum clock per sec.Q)d(α2−α1)ΔtC) Percentage in volume of a solidR)YαΔtD) Radius of circular arc of a bimetal stripS)(1/2)αΔt
View SolutionA block is hanged by means of two identical wires having cross-section area A (1mm2) as shown in the figure. If temperature is lowered by ΔT(10∘C), find the mass (in kg) to be added to hanging mass such that junction remains at its initial positions. Given that coefficient of linear expansion α=2×10−5I0C and Young's modulus Y=5×1011N/m2 for the wire.
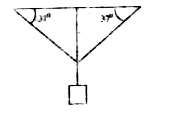
View SolutionThe coefficient of linear expansion of crystal in one direction is α1 and that in every direction perpendicular to it α2. The coefficient of cubical expansion is :
View SolutionThe centre of mass of two particles with masses 2kg and 6 kg located at (1,1,1), (2,2,1) respectively has the coordinates
View SolutionA bullet of mass 10×10−3 moving with a speed of 20ms−1 hits an ice block (0∘C) of 990g kept at rest on a frictionless floor and gets embedded in it. If ice takes 50% of K.E, the amount of ice melted (in grams) approximately is (J=4.2J/cal) (latent heat of ice=80cal/g)
View SolutionA rod of length 2 m is at a temperature of 20∘ C. find the free expansion of the rod, if the temperature is increased to 50∘C, then find stress produced when the rod is (i) fully prevented to expand, (ii) permitted to expand by 0.4mm. Y=2×1011N/m2,α=15×10−6/∘C.
View SolutionA steel rod of length 5m is fixed between two support. The coefficient of linear expansion of steel is 12.5×10−6/∘C. Calculate the stress (in 108N/m2) in the rod for an increase in temperature of 40∘C. Young's modulus for steel is 2×1011Nm−2
View SolutionA rod is fixed between two points at 20∘C. The coefficient of linear expansion of material of rod is 1.1×10−5/.C and Young's modulus is 1.2×1011N/m. Find the stress develop in the rod if temperature of rod becomes 10∘C
View SolutionAt temperature T, length of rod is L. If coefficient linear expansion of material of rod is 2×10−2/.∘C then length of rod when temperature of rod increased by 25∘C is
View SolutionA rod of length 2m is at a temperature of 20^(@)C . If the temperature is increased to 50^(@)C , then find the thermal stress developed in rod when it is fully prevented to expand (alpha=15xx10^(-6)k^(-1))
View Solutionधातु कि एक छड़, जिसका रेखीय प्रसार गुणांक 2×10−5.∘C−1 है, कि लम्बाई 20∘C पर 1 मी है । वह ताप ज्ञात कीजिए जिस पर छड़ कि लम्बाई 1 मिमी कम हो जाती है।
View SolutionA steel rod of length 50 cm has a cross–sectional area of 0.4 cm^(2) . What force would be required to stretch this rod by the same amount as the expansion produced by heating it through 10^(@)C . ( alpha = 10^(-5) k^(-1) and Y = 2 xx 10^(11) N//m^(2))
View SolutionA composite rod is made by joining a copper rod, end to end, with a second rod of a different material but of same cross-section. At 25∘C, the composite rod is 1 m in length of which the length of the copper rod is 30 cm. At 125∘C the length of the composite rod increases by 1.91 mm. The coefficient of linear expansion of copper is α=1.7×10−5∘C−1 and that of the second rod is β=n×10−5∘C−1. Find the value of n.
View SolutionA steel rod of length 5m is fixed rigidly between two supports. a of steel = 12×10−6/∘C,Y=2×1011Nm−2. With the increase in its temperature by 40∘C, the stress developed in the rod is
View SolutionA steel rod of length 5m is fixed rigidly between two supports. a of steel = 12×10−6/∘C,Y=2×1011Nm−2. With the increase in its temperature by 40∘C, the stress developed in the rod is
View Solution
