Three vectors A, B and C add upto zero. Find which is false.
(→A×→B)×→C is not zero unless →B,→C are parallel.
(→A×→B)⋅→C is not zero unless →B,→C are parallel.
If →A,→B,→C define a plane, (→A×→B)×→C is in that plane.
(→A×→B)⋅→C=∣∣→A∣∣∣∣→B∣∣∣∣→C∣∣→C2=A2+B2.
The correct Answer is:C
Step by step video, text & image solution for Three vectors A, B and C add upto zero. Find which is false. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MOTION IN A PLANE BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A PLANE EXERCISE - ASSERTION & REASON
15 Videos
- MOTION IN A PLANE BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A PLANE EXERCISE - Scalars And Vectors
5 Videos
- MOTION IN A PLANE BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A PLANE EXERCISE - HOTS
6 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Assertion And Reason
15 Videos
- MOTION IN A STRAIGHT LINEBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - NCERT Exemplar
6 Videos
Similar Questions
Knowledge Check
Three vectors A, B and C add upto zero. Find which is false.
A(→A×→B)×→C is not zero unless →B,→C are parallel.B(→A×→B)⋅→C is not zero unless →B,→C are parallel.CIf →A,→B,→C define a plane, (→A×→B)×→C is in that plane.D(→A×→B)⋅→C=∣∣→A∣∣∣∣→B∣∣∣∣→C∣∣→C2=A2+B2.
Given three vectors →a,→b and →c are non-zero and non-coplanar vectors. Then which of the following are coplanar.
View SolutionThe three vectors a, b and c with magnitude 3, 4 and 5 respectively and a+b+c=0, then the value of a.b+b.c+c.a is
View SolutionIf →a,→b,and→c be non-zero vectors such that no two are collinear or (→a×→b)×→c=13∣∣→b∣∣|→c|→a. If θ is the acute angle between vectors →band→c , then find the value of sinθ.
View SolutionThe sum of three vectors shown in figure, is zero.
(i) What is the magnitude of vector −−→OB ?
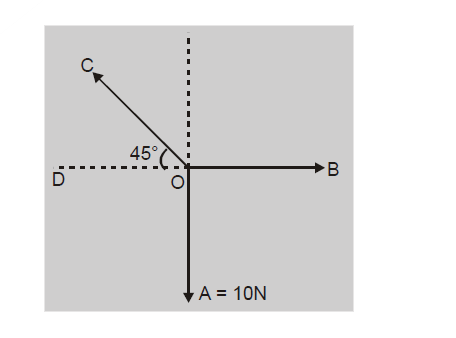
(ii) What is the magnitude of vector −−→OC ?
View SolutionLet a,b,c are three vectors of which every pair is non-collinear, if the vectors a+b and b+c are collinear with c annd a respectively, then find a+b+c.
View SolutionGive a condition that three vectors →a,→b and →c from the three sides of a triangle. What are the other possibilities?
View SolutionGive a condition that three vectors →a,→b and →c from the three sides of a triangle. What are the other possibilities?
View Solution

