The equivalent inductance of two inductances is 2.4 henry when connected in parallel and 10 henry when connected in series. The difference between the two inductance is
8 H, 2H
6H, 4H
5H, 5H
7H, 3H
The correct Answer is:B
To solve the problem of finding the difference between two inductances L1 and L2 given their equivalent inductances in parallel and series, we can follow these steps:
Step 1: Define the equations for inductance
1. When connected in parallel, the equivalent inductance Lp is given by:
1Lp=1L1+1L2
For this problem, Lp=2.4H.
2. When connected in series, the equivalent inductance Ls is given by:
Ls=L1+L2
For this problem, Ls=10H.
Step 2: Set up the equations
From the parallel combination:
12.4=1L1+1L2
This can be rearranged to:
L1L2=2.4(L1+L2)
From the series combination:
L1+L2=10
Step 3: Substitute and simplify
Let L1+L2=10 (Equation 1) and L1L2=2.4×10=24 (Equation 2).
Step 4: Solve the equations
From Equation 1, we can express L2 in terms of L1:
L2=10−L1
Substituting L2 in Equation 2:
L1(10−L1)=24
Expanding this gives:
10L1−L21=24
Rearranging leads to:
L21−10L1+24=0
Step 5: Solve the quadratic equation
Using the quadratic formula L1=−b±√b2−4ac2a:
Here, a=1,b=−10,c=24:
L1=10±√(−10)2−4⋅1⋅242⋅1
L1=10±√100−962
L1=10±22
Thus, we have:
L1=6orL1=4
Step 6: Find L2
Using L1+L2=10:
- If L1=6, then L2=4.
- If L1=4, then L2=6.
Step 7: Find the difference
The difference between the two inductances is:
|L1−L2|=|6−4|=2H
Final Answer
The difference between the two inductances is 2H.
---
1. When connected in parallel, the equivalent inductance Lp is given by:
1Lp=1L1+1L2
For this problem, Lp=2.4H.
Ls=L1+L2
For this problem, Ls=10H.
From the parallel combination:
12.4=1L1+1L2
This can be rearranged to:
L1L2=2.4(L1+L2)
L1+L2=10
Let L1+L2=10 (Equation 1) and L1L2=2.4×10=24 (Equation 2).
From Equation 1, we can express L2 in terms of L1:
L2=10−L1
L1(10−L1)=24
Expanding this gives:
10L1−L21=24
Rearranging leads to:
L21−10L1+24=0
Using the quadratic formula L1=−b±√b2−4ac2a:
Here, a=1,b=−10,c=24:
L1=10±√(−10)2−4⋅1⋅242⋅1
L1=10±√100−962
L1=10±22
Thus, we have:
L1=6orL1=4
Using L1+L2=10:
- If L1=6, then L2=4.
- If L1=4, then L2=6.
The difference between the two inductances is:
|L1−L2|=|6−4|=2H
The difference between the two inductances is 2H.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBook:NCERT FINGERTPS ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:EXEMPLAR PROBLEMS
Explore 3 Videos
- ELECTROMAGNETIC INDUCTIONBook:NCERT FINGERTPS ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:ASSERTION AND REASON
Explore 15 Videos
- ELECTRIC CHARGES AND FIELDSBook:NCERT FINGERTPS ENGLISHChapter:ELECTRIC CHARGES AND FIELDSExercise:Assertion And Reason
Explore 15 Videos
- ELECTROMAGNETIC WAVESBook:NCERT FINGERTPS ENGLISHChapter:ELECTROMAGNETIC WAVESExercise:Assertion And Reason
Explore 15 Videos
Similar Questions
The equivalent inductance between A and B is
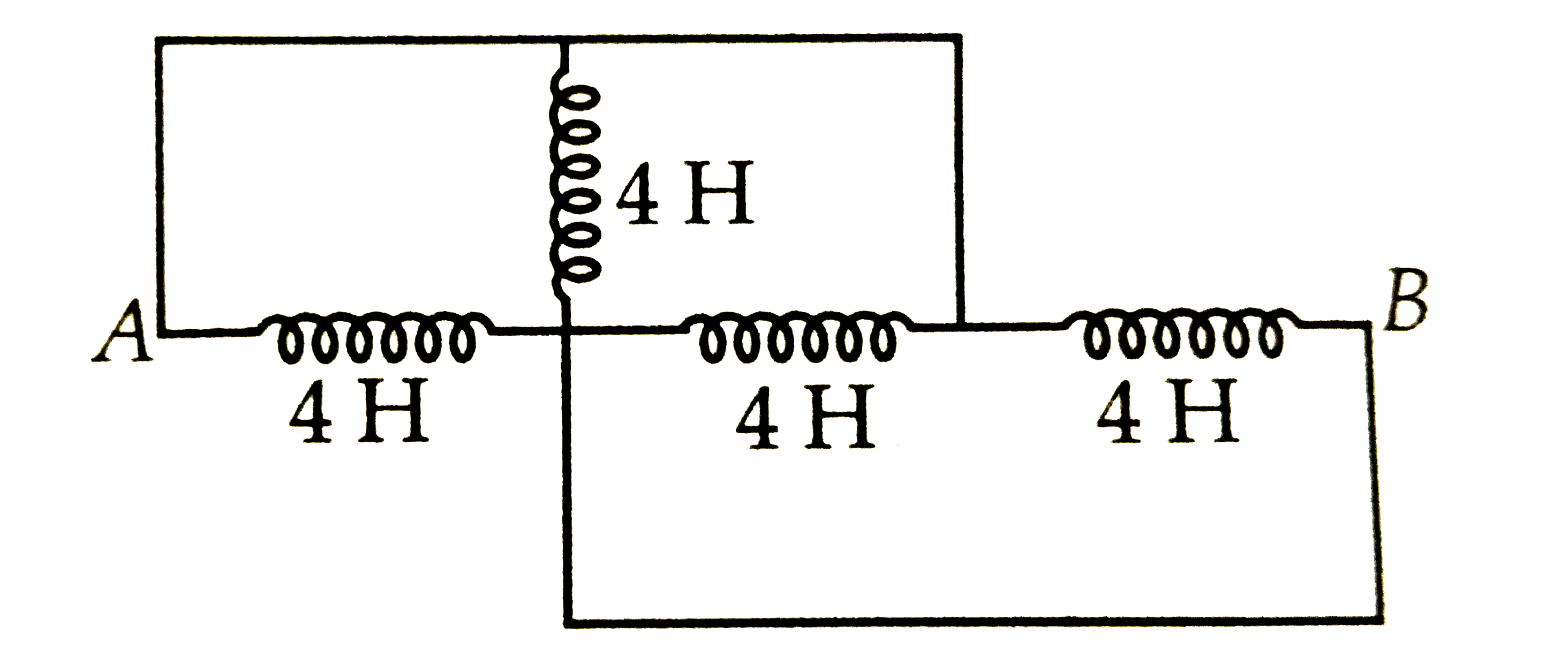
View SolutionThe equivalent inductance between points P and Q in the figure is

View SolutionCalculate the equivalent resistance between the points A and B in Fig.
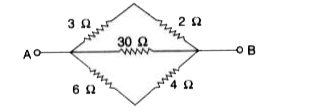
View SolutionTwo inductors each of inductance L are connected in parallel. One more inductor of value 5 mH is connected in series of this configuration then the effective inductance is 15 mH . The value of L is ………..mH.
View SolutionThe equivalent inductance between points P and Q in the figure is :
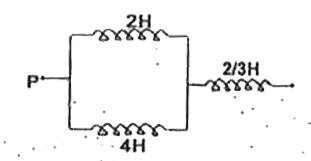
View SolutionTwo inductances connected in parallel are equivalent to a single inductance of 1.5H and when connected in series are equivalent to a single inductance of 8 H. The difference in their inductance is
View SolutionThe equivalent inductance between points P and Q in figure is :
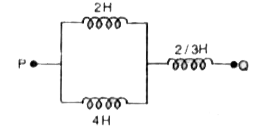
View SolutionFind inductive reactance of the inductor when it is connected in D.C. circuit.
View SolutionConsider two capacitors :C1=10μC and C2=40μF. What is the equivalent capacitance if the two are connected.
(1) in parallel ?
(2) in series ?
(3) If the two are connected in series to a 9.0 volt battery what are the charges Q1 and Q2 stored on the two capacitors ?
View SolutionA coil of resistance 200 ohms and self inductance 1.0 henry has been connected in series to an a.c. source of frequency 200πHz. The phase difference between voltage and current is
View Solution