In a uniform magneitc field of induced B a wire in the form of a semicircle of radius r rotates about the diameter of hte circle with an angular frequency ω. The axis of rotation is perpendicular to hte field. If the total resistance of hte circuit is R, the mean power generated per period of rotation is
Bπr2ω2R
(Bπr2ω)28R
(Bπrω)22R
(Bπrω2)28R
The correct Answer is:B
To solve the problem step by step, we will follow the concepts of electromagnetic induction and the formulas related to induced EMF and power.
Step 1: Understand the Setup
We have a semicircular wire of radius r rotating in a uniform magnetic field B with an angular frequency ω. The axis of rotation is perpendicular to the magnetic field.
Step 2: Calculate the Area of the Semicircle
The area A of a semicircle is given by:
A=12πr2
Step 3: Determine the Magnetic Flux
The magnetic flux Φ through the semicircular wire is given by:
Φ=B⋅A⋅cos(θ)
where θ=ωt (the angle between the magnetic field and the normal to the area). Substituting the area:
Φ=B⋅(12πr2)⋅cos(ωt)=12Bπr2cos(ωt)
Step 4: Calculate the Induced EMF
The induced EMF E can be calculated using Faraday's law of electromagnetic induction:
E=−dΦdt
Differentiating the flux:
E=−ddt(12Bπr2cos(ωt))
Using the chain rule:
E=−12Bπr2⋅(−ωsin(ωt))=12Bπr2ωsin(ωt)
Step 5: Calculate the Instantaneous Power
The instantaneous power P is given by:
P=E2R
Substituting the expression for E:
P=(12Bπr2ωsin(ωt))2R=B2π2r4ω2sin2(ωt)4R
Step 6: Calculate the Mean Power
To find the mean power over one complete cycle, we need to take the average of sin2(ωt). The average value of sin2(ωt) over one period is 12:
Pmean=B2π2r4ω24R⋅12=B2π2r4ω28R
Final Answer
Thus, the mean power generated per period of rotation is:
Pmean=B2π2r4ω28R
We have a semicircular wire of radius r rotating in a uniform magnetic field B with an angular frequency ω. The axis of rotation is perpendicular to the magnetic field.
The area A of a semicircle is given by:
A=12πr2
The magnetic flux Φ through the semicircular wire is given by:
Φ=B⋅A⋅cos(θ)
where θ=ωt (the angle between the magnetic field and the normal to the area). Substituting the area:
Φ=B⋅(12πr2)⋅cos(ωt)=12Bπr2cos(ωt)
The induced EMF E can be calculated using Faraday's law of electromagnetic induction:
E=−dΦdt
Differentiating the flux:
E=−ddt(12Bπr2cos(ωt))
Using the chain rule:
E=−12Bπr2⋅(−ωsin(ωt))=12Bπr2ωsin(ωt)
The instantaneous power P is given by:
P=E2R
Substituting the expression for E:
P=(12Bπr2ωsin(ωt))2R=B2π2r4ω2sin2(ωt)4R
To find the mean power over one complete cycle, we need to take the average of sin2(ωt). The average value of sin2(ωt) over one period is 12:
Pmean=B2π2r4ω24R⋅12=B2π2r4ω28R
Thus, the mean power generated per period of rotation is:
Pmean=B2π2r4ω28R
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXEMPLAR PROBLEMS
3 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - ASSERTION AND REASON
15 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Assertion And Reason
15 Videos
- ELECTROMAGNETIC WAVESBOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Assertion And Reason
15 Videos
Similar Questions
A wire is bent to form a semi-circle of radius a. the wire rotates about its one end with angular velocity ω.Axis of rotation being perpendicular to plane of the semicircle . In the space , a uniform magnetic field of induction B exists along the axis of rotation as shown . The correct statement is :
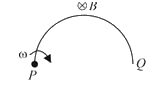
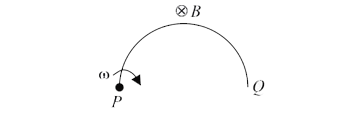
View SolutionA wire is bent to form a semi-circle of radius a. The wire rotates about its one end with angular velocity ω. Axis of rotation being perpendicular to plane of the semicircle. In the space, a uniform magnetic field of induction exists along the axis of rotation as shown. The correct statement is
View Solution
Knowledge Check
A solid cylinder of mass M and radius R rotates about its axis with angular speed ω. Its rotational kinetic energy is
A12MR2ω2BMR2ω2C14MR2ω2D18MR2ω2
A conducting circular loop of radius r is rotated about its diameter at a constant angular velocity ω in a magnetic field B perpendicular to the axis of rotation. In what position of the loop is the induced emf zero?
View SolutionA solid sphere of radius r and mass m rotates about an axis passing through its centre with angular velocity ω. Its K.E. Is
View SolutionA uniform circular loop of radius a and resistance R palced perpendicular to a uniform magnetic field B. One half of the loop is rotated about the diameter with angular velocity ω as shown in Fig. Then, the current in the loop is

View SolutionA uniform circular loop of radius a and resistance R palced perpendicular to a uniform magnetic field B. One half of the loop is rotated about the diameter with angular velocity ω as shown in Fig. Then, the current in the loop is

View SolutionA rectangular coil of area A rotates in a uniform magnetic field B with angular velocity about an axis perpendicular to the field, initially the plane of coil is perpendicular to the field,then the avarage induced e.m.f. after rotating by 90° is
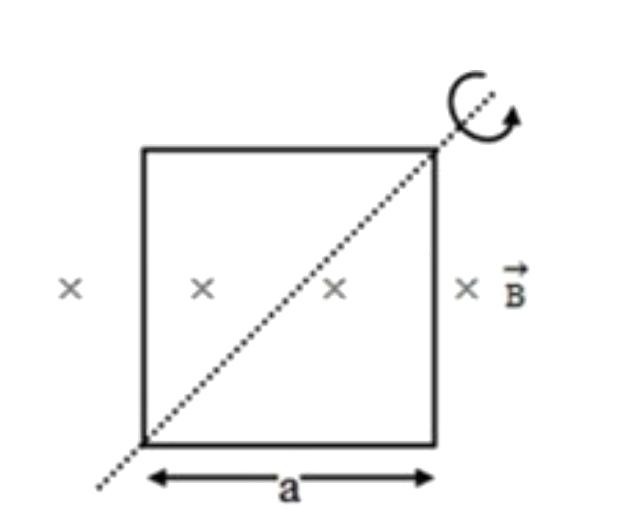
View SolutionA square loop of side a is rotating about its diagonal with angular velocity ω in a perpendicular magnetic field →B It has 10 turns. The emf induced is
View SolutionA conducting rod OA of length l is rotated about its end O with an angular velocity ω in a uniform magnetic field directed perpendicualr to the rotation. Find the emf induced in the rod, between it's ends.
View Solution
