A galvanometer has a current sensitivity of 1 mA per division. A variable shunt is connected across the galvanometer and the combination is put in series with a resistance of 500Ω and cell of internal resistance 1Ω. It gives a deflection of 5 division for shunt of 5 ohm and 20 division for shunt of 25 ohm. The emf of cell is
47.1 V
57.1 V
67.1 V
77.1 V
The correct Answer is:A
To solve the problem, we need to find the emf of the cell given the current sensitivity of the galvanometer, the shunt resistances, and the deflections observed. Here’s a step-by-step solution:
Step 1: Understand the Circuit Configuration
We have a galvanometer connected in parallel with a shunt resistor (S), and this combination is in series with a total resistance (R) of 500Ω and the internal resistance (r) of the cell which is 1Ω.
Step 2: Define the Variables
- Let I be the total current from the cell.
- Let Ig be the current through the galvanometer.
- The current through the shunt resistor S is I−Ig.
Step 3: Use the Current Sensitivity of the Galvanometer
The galvanometer has a current sensitivity of 1 mA per division.
- For the first case with a shunt of 5Ω and a deflection of 5 divisions:
Ig=5mA=0.005A
- For the second case with a shunt of 25Ω and a deflection of 20 divisions:
Ig=20mA=0.020A
Step 4: Apply Kirchhoff's Law
The voltage across the galvanometer is equal to the voltage across the shunt:
Ig⋅G=(I−Ig)⋅S
Where G is the resistance of the galvanometer.
Step 5: Write the Equations for Each Case
1. For the first case (shunt = 5Ω, deflection = 5 divisions):
0.005⋅G=(I−0.005)⋅5
Rearranging gives:
I=0.005⋅G5+0.005
2. For the second case (shunt = 25Ω, deflection = 20 divisions):
0.020⋅G=(I−0.020)⋅25
Rearranging gives:
I=0.020⋅G25+0.020
Step 6: Set the Two Equations for I Equal
Set the expressions for I from both cases equal to each other:
0.005⋅G5+0.005=0.020⋅G25+0.020
Step 7: Solve for G
Cross-multiply and simplify to find G.
Step 8: Calculate the Emf of the Cell
Using the total resistance in the circuit:
E=I⋅(R+r)+Ig⋅G
Substituting the values of I and Ig from the equations derived earlier will give us the emf E.
Step 9: Final Calculation
After substituting and solving, we find:
E≈47.13V
Final Answer
The emf of the cell is approximately 47.13 V.
---
We have a galvanometer connected in parallel with a shunt resistor (S), and this combination is in series with a total resistance (R) of 500Ω and the internal resistance (r) of the cell which is 1Ω.
- Let I be the total current from the cell.
- Let Ig be the current through the galvanometer.
- The current through the shunt resistor S is I−Ig.
The galvanometer has a current sensitivity of 1 mA per division.
- For the first case with a shunt of 5Ω and a deflection of 5 divisions:
Ig=5mA=0.005A
- For the second case with a shunt of 25Ω and a deflection of 20 divisions:
Ig=20mA=0.020A
The voltage across the galvanometer is equal to the voltage across the shunt:
Ig⋅G=(I−Ig)⋅S
Where G is the resistance of the galvanometer.
1. For the first case (shunt = 5Ω, deflection = 5 divisions):
0.005⋅G=(I−0.005)⋅5
Rearranging gives:
I=0.005⋅G5+0.005
0.020⋅G=(I−0.020)⋅25
Rearranging gives:
I=0.020⋅G25+0.020
Set the expressions for I from both cases equal to each other:
0.005⋅G5+0.005=0.020⋅G25+0.020
Cross-multiply and simplify to find G.
Using the total resistance in the circuit:
E=I⋅(R+r)+Ig⋅G
Substituting the values of I and Ig from the equations derived earlier will give us the emf E.
After substituting and solving, we find:
E≈47.13V
The emf of the cell is approximately 47.13 V.
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISM BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - EXEMPLAR PROBLEMS
6 Videos
- MOVING CHARGES AND MAGNETISM BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - ASSERTION & REASON
15 Videos
- MOVING CHARGES AND MAGNETISM BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - Assertion And Reason
15 Videos
- MAGNETISM AND MATTER BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - NCERT Exemplar
5 Videos
- NUCLEIBOOK - NCERT FINGERTPS ENGLISHCHAPTER - NUCLEIEXERCISE - Assertion And Reason
15 Videos
Similar Questions
A galvanometer having 50 divisions provided with a variable shunt S is used to measure the current when connected in series with a resistance of 90Ω and a battery of internal resistance 10Ω. It is observed that when the shunt resistances are 10Oemga and 50Ω, the deflections are, respectively, 9 and 30 divisions. What is the resistance of the galvanometer
View SolutionA galvanometer vaving 50 divisions provided with a variable shunt S is used to measure the current when conneted in series with a resistance of 90Ω and a battery of internal resistance 10Ω. It is observed that when the snt resistaces are 10Ω&70Ω respectively, the deflection are respectively 9 and 30 dividions. What is the resistance of the galvanometer ? Further, if the full scale deflection of the galvanometer movement require 200 mA. find the emf of the cell.
View Solution
Knowledge Check
If the galvanometer current is 10 mA, resistance of the galvanometer is 40Ω and shunt of 2Ω is connected to the galvanometer, the maximum current which can be measured by this ammeter is
A0.21AB2.1AC210AD21A
The galvanometer shown in the figure has resistance 10Ω. It is shunted by a series combination of a resistance S=1Ω and an ideal cell of emf 2 V. A current 2 A passes as shown.
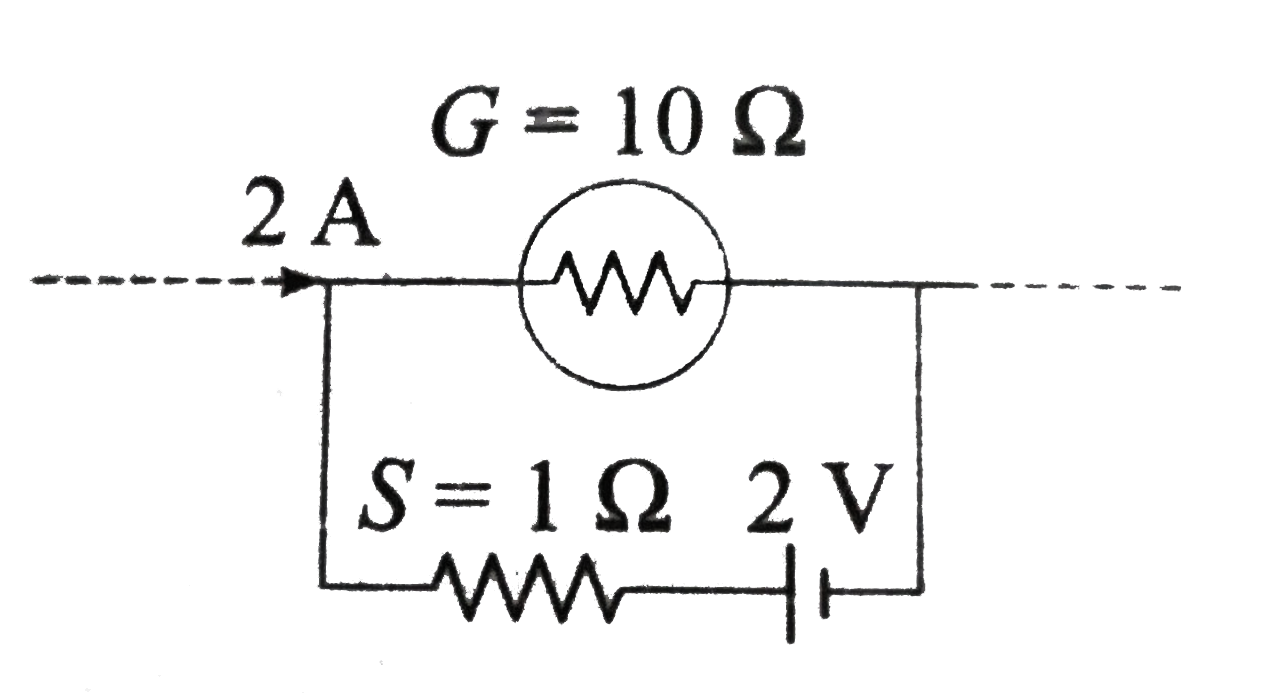

View SolutionA galvanometer of resistance 40Ω and current passing through it is 100μA per divison. The full scale has 50 divisions. If it is converted into an ammeter of range 2A by using a shunt, then the resistance of ammeter is
View SolutionThe senstivity of a galvanometer that measures current is decreased by 1/40 times by using shunt resistance of 10Ω . Then, the value of the resistance of the galvanometer is
View SolutionA galvanometer coil has a resistance of 100Ω. When a current passes through the galvanometer, 1% of the current goes through the coil and the rest through the shunt. Find the resistance of the shunt.
View SolutionA galvanometer has a resistance of 98Ω. If 2% of the main current is to be passed through the meter what should be the value of the shunt?
View SolutionDeflection of galvanometer in the circuit is 71 divisions. A shunt of 15Ω is connected parallel to galvanometer and value of R is adjusted such that main current ramains the same. If the deflection in the galvanometer falls to 15 divisions then the resistance G of galvanometer in (in ohm)

View SolutionThe sensitivity of a galvanometer is 60 divisions/Amp. When a shunt is used, its sensitivity becomes 10 divisions/amp. If galvanometer is of resistance 20Ω, · the value of shunt used is :
View Solution
