The senstivity of a galvanometer that measures current is decreased by 1/40 times by using shunt resistance of 10Ω . Then, the value of the resistance of the galvanometer is
400Ω
410Ω
30Ω
390Ω
The correct Answer is:D
To find the resistance of the galvanometer, we can follow these steps:
1. Understanding Sensitivity:
The sensitivity of a galvanometer is defined as the deflection (θ) per unit current (i). We denote the initial sensitivity as S1=θi1.
2. Sensitivity After Shunt Connection:
When a shunt resistance (R_s) is connected, the sensitivity decreases by a factor of 140. Therefore, the new sensitivity S2 can be expressed as:
S2=S140
3. Relating Currents:
From the sensitivity definitions, we can relate the currents:
S2=θi2⟹i2=40⋅i1
4. Current Distribution:
When the shunt of resistance Rs=10Ω is connected, the total current i2 splits between the galvanometer and the shunt. The current through the shunt is:
is=i2−i1=40⋅i1−i1=39⋅i1
5. Voltage Across the Galvanometer:
The voltage across the galvanometer (V_g) can be expressed as:
Vg=i1⋅G
where G is the resistance of the galvanometer.
6. Voltage Across the Shunt:
The voltage across the shunt can also be expressed as:
Vs=is⋅Rs=(39⋅i1)⋅10=390⋅i1
7. Equating Voltages:
Since both the galvanometer and the shunt have the same voltage across them when connected in parallel, we can equate the two expressions:
i1⋅G=390⋅i1
8. Solving for G:
Dividing both sides by i1 (assuming i1≠0):
G=390Ω
Final Answer:
The resistance of the galvanometer is G=390Ω.
---
The sensitivity of a galvanometer is defined as the deflection (θ) per unit current (i). We denote the initial sensitivity as S1=θi1.
When a shunt resistance (R_s) is connected, the sensitivity decreases by a factor of 140. Therefore, the new sensitivity S2 can be expressed as:
S2=S140
From the sensitivity definitions, we can relate the currents:
S2=θi2⟹i2=40⋅i1
When the shunt of resistance Rs=10Ω is connected, the total current i2 splits between the galvanometer and the shunt. The current through the shunt is:
is=i2−i1=40⋅i1−i1=39⋅i1
The voltage across the galvanometer (V_g) can be expressed as:
Vg=i1⋅G
where G is the resistance of the galvanometer.
The voltage across the shunt can also be expressed as:
Vs=is⋅Rs=(39⋅i1)⋅10=390⋅i1
Since both the galvanometer and the shunt have the same voltage across them when connected in parallel, we can equate the two expressions:
i1⋅G=390⋅i1
Dividing both sides by i1 (assuming i1≠0):
G=390Ω
The resistance of the galvanometer is G=390Ω.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-III49videos
MOVING CHARGES AND MAGNETISM
- BOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-IB71videos
MOVING CHARGES AND MAGNETISM
- BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - very Short answer type question15videos
MOTION IN A STRAIGHT LINE
- BOOK - AAKASH SERIESCHAPTER - NUCLEAR PHYSICSEXERCISE - ADDITIONAL PRACTICE PRACTICE SHEET (ADVANCED) Integer Type Questions3videos
NUCLEAR PHYSICS
Similar Questions
Knowledge Check
- Question 1 - Select One
A galvanometer of resistance 70Ω, is converted to an ammeter by a shunt resistance r3=0.03Ω. The value of its resistance will become
A0.025ΩB0.022ΩC0.035ΩD0.030Ω
In an experiment to determine the resistance of a galvanometer by half deflection method, the circuit shown is used. In one set of readings , if R=10ΩS=4Ω, then the resistance of the galvanometer is
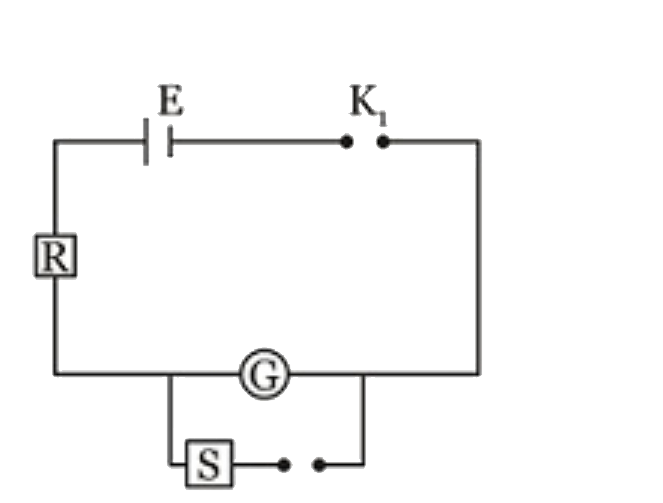 View Solution
View SolutionWhen 0.005A current flows through a moving coil galvanometer, it gives fullscale deflection. It is converted into a voltmeter to read 5 Volt, using an external resistance of 975Ω. The resistance of galvanometer in ohms is
View SolutionA galvanometer measures current which passes through it. A galanometer can measure typically carrent of order of mA. To be able to measure currents of the order of amperes of main current, a shunt resistance 'S' is connected in parallel with galvanometer.
If resistance of galavonometer is 10Ω and maximum current ig is 10mA then the shunt resistance required so that the main current 'I' can be upto 1A is (in Ω)View SolutionA moving coil galvanometer has 50 turns and each turn has an area 210 . The magnetic field produced by the magnet inside the galvanometer is 0.02 . The torsional constant of the suspension wire is 10 . When a current flows through the galvanometer, a full scale deflection occurs if the coil rotates by 0.2 . The resistance of the coil of the galvanometer is 50 . This galvanometer is to be converted into an ammeter capable of measuring current in the range 01.0 . For this purpose, a shunt resistance is to be added in parallel to the galvanometer. The value of this shunt resistance, in , is __________.
View SolutionAn ohm meter measures the resistance placed between its leads. This resistance reading is indicated by a galvanometer that operates on current. The ohm meter has an internal source of voltage to create the necessary current to operate the galvanometer and also has approproate resistor to allow just right amount of current through galvanometer. A simple ohm meter is shown here.
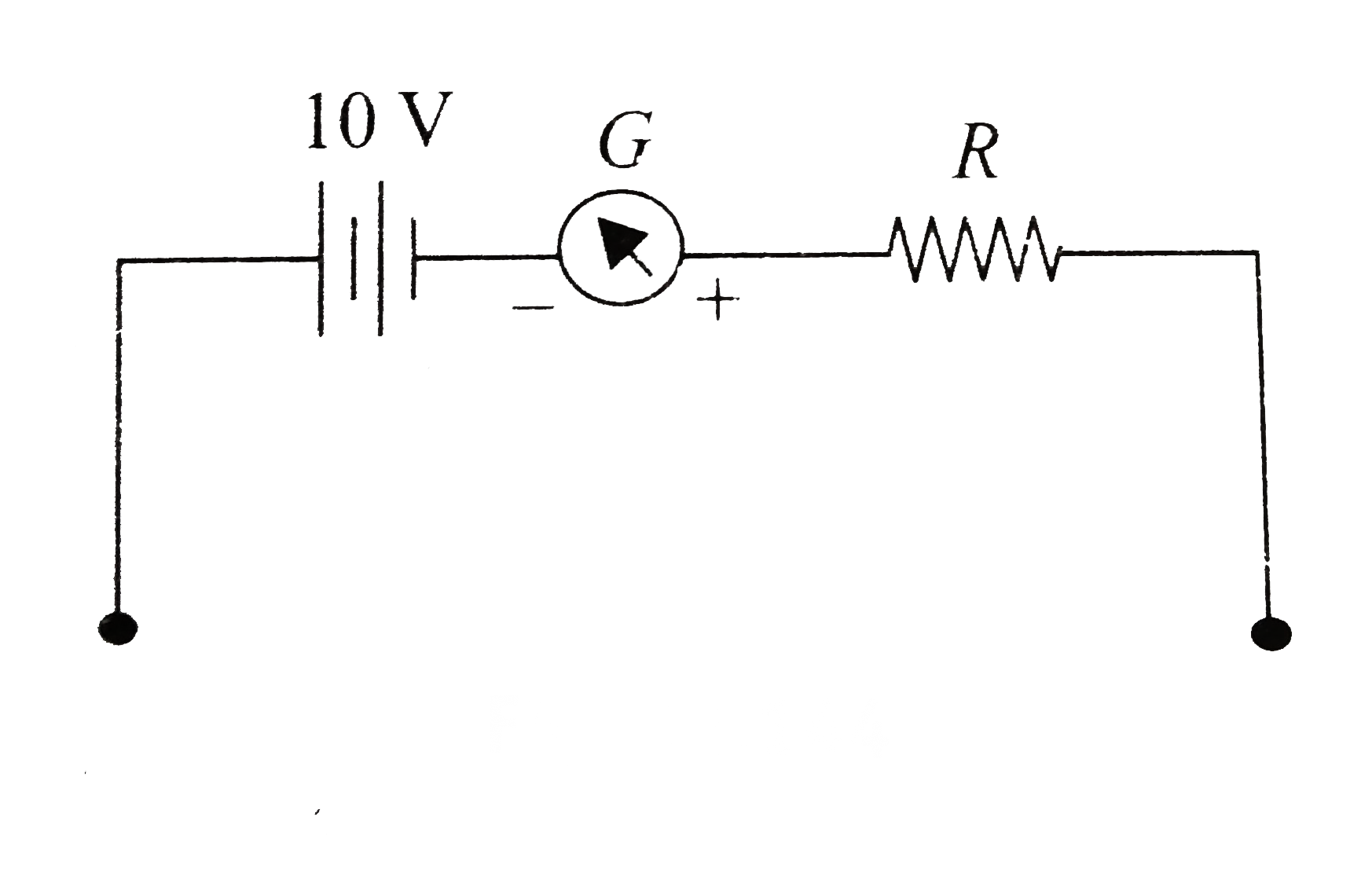
When there is an infinite resistance, there is zero current through galvanometer and it points in middle. If the test leads of this meter are directly shorted, (zero resistance) galvanometer will give full deflection.
Galvanometer specification
Resistance of galvanometer =100Ω
Fullscale current =0.5mA
Total number of division =40 .
View SolutionWhen a current of 5mA is passed through a galvanometer having a coil of resistance 15Ω, it shows full sacle deflection. The value of the resistance to be put in series with the galvanometer to convert it into a voltmeter of range 0−10V is:
View SolutionAn ohm meter measures the resistance placed between its leads. This resistance reading is indicated by a galvanometer that operates on current. The ohm meter has an internal source of voltage to create the necessary current to operate the galvanometer and also has approproate resistor to allow just right amount of current through galvanometer. A simple ohm meter is shown here.
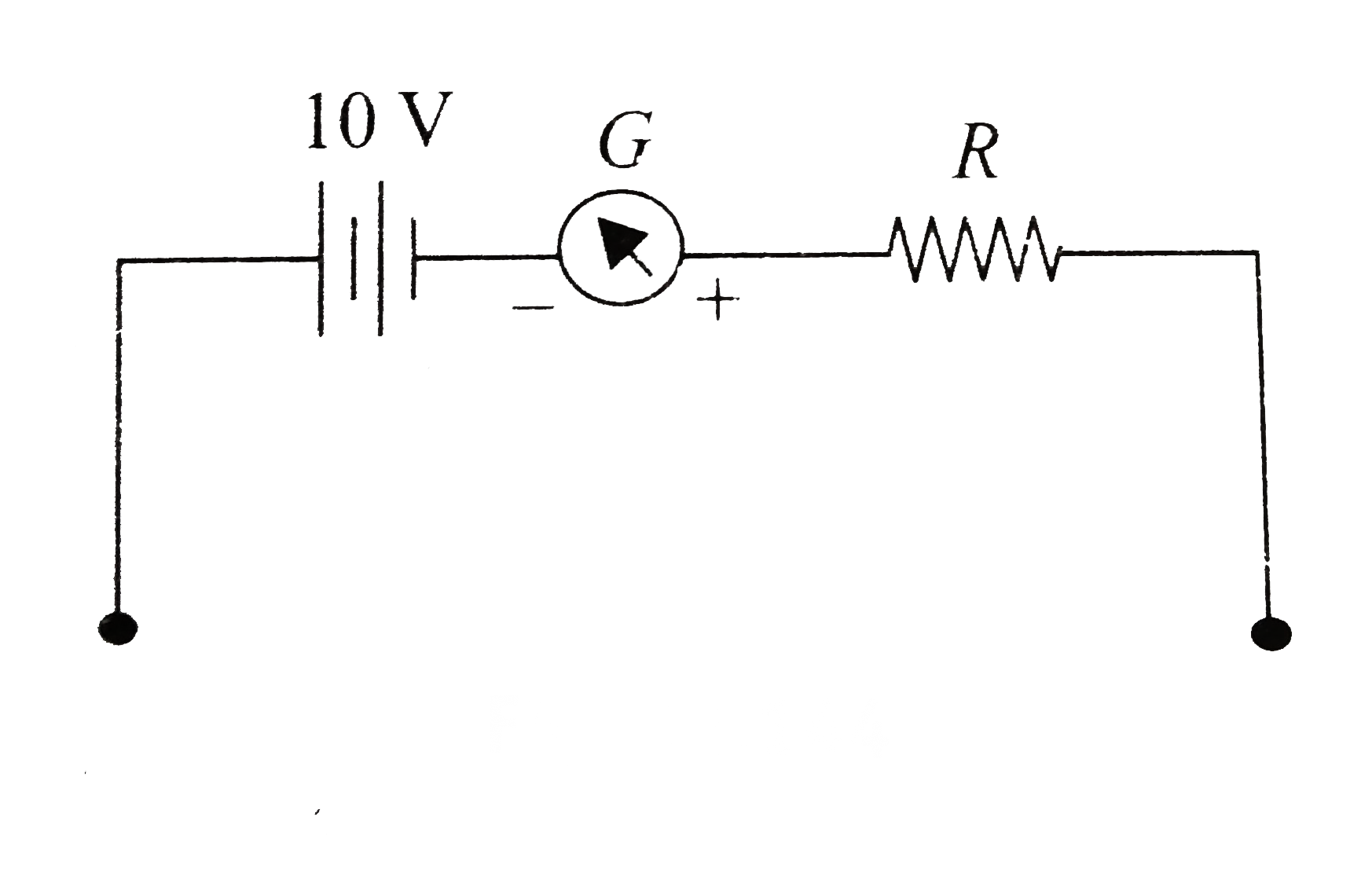
When there is an infinite resistance, there is zero current through galvanometer and it points in middle. If the test leads of this meter are directly shorted, (zero resistance) galvanometer will give full deflection.
Galvanometer specification
Resistance of galvanometer =100Ω
Fullscale current =0.5mA
Total number of division =40 .
if we want to measure 5 Omega Resistance than what is the position of needleView Solution
