A strong magnetic field is applied on a stationary electron, then
moves in the direction of the field.
remained stationary.
moves perpendicular to the direction of the field.
moves opposite to the direction of the field.
The correct Answer is:B
To solve the question, we need to analyze the situation where a strong magnetic field is applied to a stationary electron. Here’s the step-by-step solution:
Step 1: Understand the scenario
We have a stationary electron, which means its initial velocity (V) is zero. The magnetic field (B) is applied in a certain direction.
Hint: Remember that the motion of a charged particle in a magnetic field depends on its velocity.
Step 2: Recall the formula for magnetic force
The force (F) experienced by a charged particle in a magnetic field is given by the formula:
F=Q(→V×→B)
where:
- Q is the charge of the particle,
- →V is the velocity vector of the particle,
- →B is the magnetic field vector.
Hint: The cross product indicates that the force is dependent on both the velocity and the magnetic field direction.
Step 3: Substitute the values
Since the electron is stationary, its velocity →V=0. Therefore, we can substitute this into the formula:
F=Q(0×→B)
Hint: Think about what happens to the force when the velocity is zero.
Step 4: Calculate the force
From the substitution, we find:
F=Q⋅0=0
This means that the force acting on the electron is zero.
Hint: A zero force means there is no change in motion.
Step 5: Conclusion
Since the force is zero, the stationary electron will remain stationary even when a magnetic field is applied. Therefore, the correct answer to the question is that the electron will remain stationary.
Final Answer: The electron remains stationary (Option B).
We have a stationary electron, which means its initial velocity (V) is zero. The magnetic field (B) is applied in a certain direction.
The force (F) experienced by a charged particle in a magnetic field is given by the formula:
F=Q(→V×→B)
where:
- Q is the charge of the particle,
- →V is the velocity vector of the particle,
- →B is the magnetic field vector.
Since the electron is stationary, its velocity →V=0. Therefore, we can substitute this into the formula:
F=Q(0×→B)
From the substitution, we find:
F=Q⋅0=0
Since the force is zero, the stationary electron will remain stationary even when a magnetic field is applied. Therefore, the correct answer to the question is that the electron will remain stationary.
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISM BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - HOTS
5 Videos
- MOVING CHARGES AND MAGNETISM BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - EXEMPLAR PROBLEMS
6 Videos
- MAGNETISM AND MATTER BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - NCERT Exemplar
5 Videos
- NUCLEIBOOK - NCERT FINGERTPS ENGLISHCHAPTER - NUCLEIEXERCISE - Assertion And Reason
15 Videos
Similar Questions
An electron accelerated by a potential difference 2.5 kV moves horizontally into a region of space in which there is a downward directed uniform electric field of magnitude 10kVm−1.
(a) In what direction must a magnetic field be applied so that the electron moves undeflected? Ignore the gravitational force. What is the magnitude of the smallest magnetic field possible in this case?
(b) What happens if the charge is a proton that passes through the same combination of fields ?
View SolutionA uniform magnetic field exists in a circular region of radius r.The magnitude of magnetic field is B and points inward.An electron flies into the region radially as shown in figure.After a certain time, the electron deflected by the magnetic field leaves the region.The time interval during which the electron moves in the region is Nmtan−1eBrmVeB.Then find value of N.(m is mass of electron and e is charge of electron)
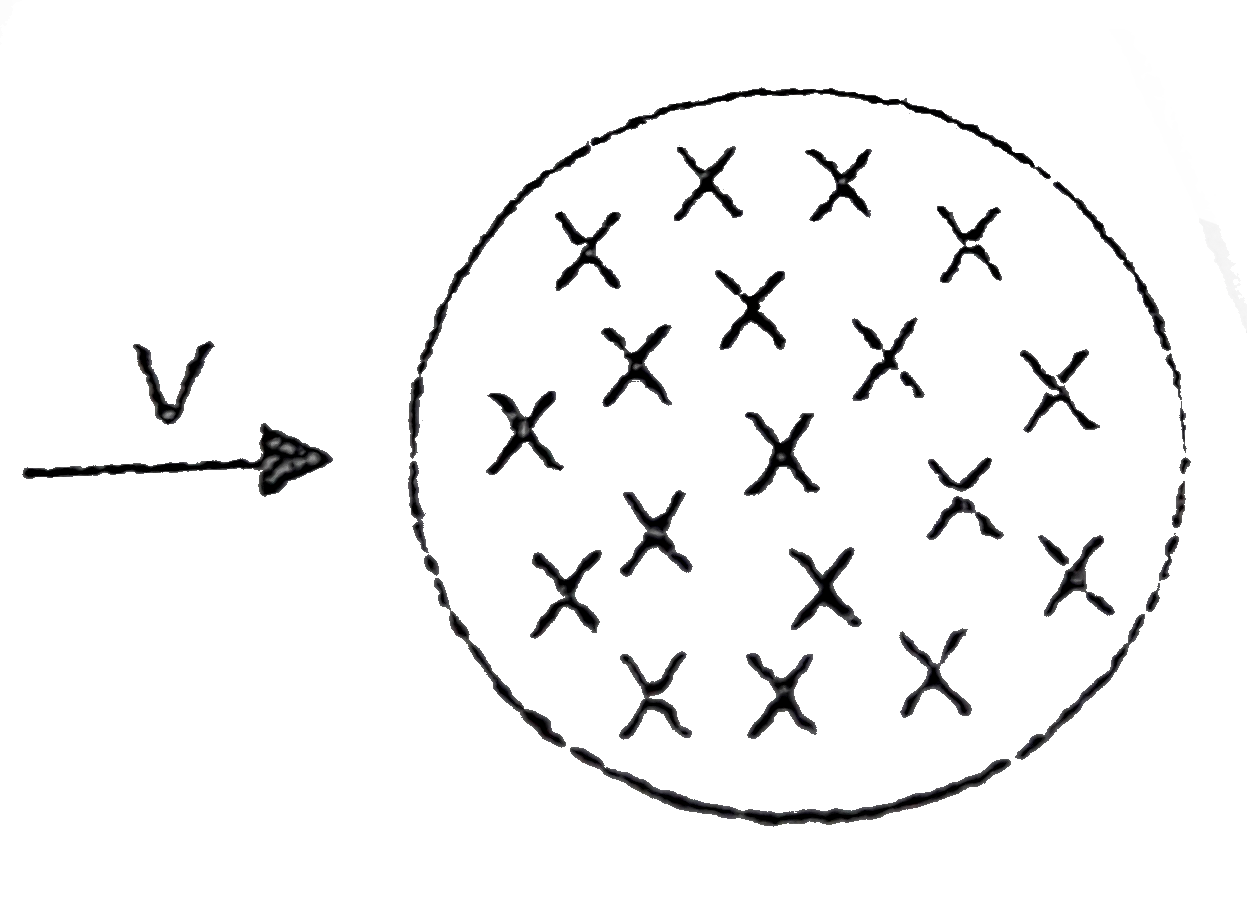
View SolutionWhy a thick metal plate oscillating about a horizontal axis stops when a strong magnetic field is applied on the plane?
View SolutionStrong magnetic fields and non-ionising radiations are used in
View SolutionSTATEMENT - 1 : By making suitable arrangement, a magnetic field can cause a stationary charge to accelerate.
and
STATEMENT - 2 : A constant magnetic field cannot interact with stationary chrages.
View SolutionA metallic rod of mass m length R is pivoted at O. It is free to rotate about a horizontal axis passing through O . An inward magnetic field is applied as shown in the figure. Find the ratio of maximum electric field inside the metallic rod to the applied magnetic field induction .

View SolutionThe Betatron was the first important machine for producing high energy electrons. The action of the betatron depends on the same fundamental principle as that of the transformer in which an alternating current applied to a primary coil induces an altermating current usually with higher or lower voltage in the secondary coil. In the betatron secondary coil is replaced by a doughnut shaped vacuum chamber.Electron produced in the doughnut from a hot filament, are given a preliminary acceleration by the application of an electric field having potential difference of 20kV to 70kV, when an alternating magnetic field is applied parallel to the axis of the tube, two effects are produced (1) an electromotive force is produced in the electron orbit by the changing magnetic flux that gives an additional energy to the electrons (2) a radial force is produced by the action of magnetic field whose direction is perpendicular to the electron velocity. Which keeps the electron moving in a circular path. Conditions are arranged such that the increasing magnetic field keeps the electron in a circular orbit of constant radius. The mathematical relation between the betatron parameters to ensure the above condition is called BETATRON condition.
If the orbit radius of the circular path traced by the electron is R, magnetic field is B, speed of the electron is v, mass of the electron is m, charge on the electron is e and ϕ is the flux within the orbit of radius R. Then answer the following questions based on the above comprehension.
What is the tangential force acting on the electron ?
View SolutionShows a coil placed in a decreasing magnetic field applied perpendicular to the plane of the coil. The magnetic field is decreasing at a rate of 10Ts−1. Find out current in magnitude and direction of current.

View SolutionShows a coil placed in a decreasing magnetic field applied perpendicular to the plane of the coil. The magnetic field is decreasing at a rate of 10Ts−1. Find out current in magnitude and direction of current.

View SolutionThe Betatron was the first important machine for producing high energy electrons. The action of the betatron depends on the same fundamental principle as that of the transformer in which an alternating current applied to a primary coil induces an altermating current usually with higher or lower voltage in the secondary coil. In the betatron secondary coil is replaced by a doughnut shaped vacuum chamber.Electron produced in the doughnut from a hot filament, are given a preliminary acceleration by the application of an electric field having potential difference of 20kV to 70kV, when an alternating magnetic field is applied parallel to the axis of the tube, two effects are produced (1) an electromotive force is produced in the electron orbit by the changing magnetic flux that gives an additional energy to the electrons (2) a radial force is produced by the action of magnetic field whose direction is perpendicular to the electron velocity. Which keeps the electron moving in a circular path. Conditions are arranged such that the increasing magnetic field keeps the electron in a circular orbit of constant radius. The mathematical relation between the betatron parameters to ensure the above condition is called BETATRON condition.
If the orbit radius of the circular path traced by the electron is R, magnetic field is B, speed of the electron is v, mass of the electron is m, charge on the electron is e and ϕ is the flux within the orbit of radius R. Then answer the following questions based on the above comprehension.
What is the BETATRON condition ?
View Solution
