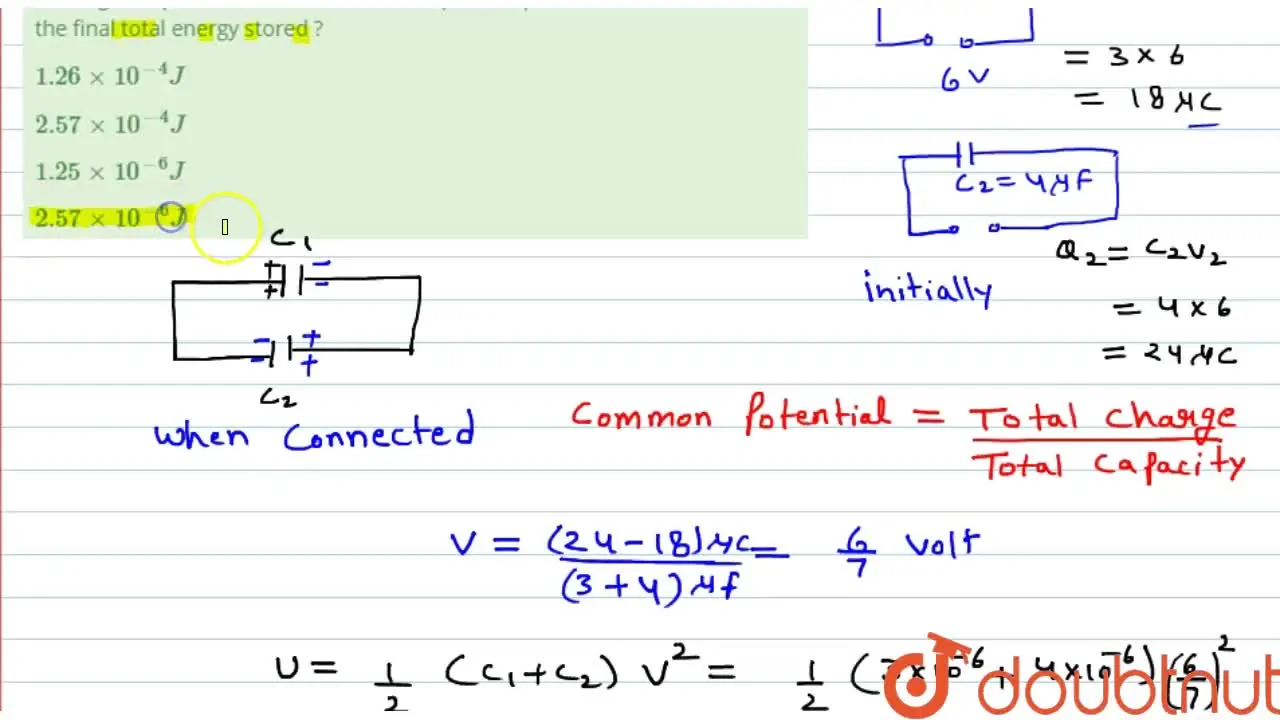
Two capcitors, 3 and are individually charged across a 6 V battery. After being disconnected from the battery, they are connected together with the negative plate of one attached to the positive plate of the other. What is the final total energy stored ?
The correct Answer is:D
As Q = CV
Initially the charge on each capacitor is
and
When two capacitor is are joined to each other such that negative plate of one is attached with the positive plate of the other . The charges and are redistributed till they attain the common potential which is given by .
Common potential
Final energy stored,
Related Playlists
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - HOTS5videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - EXEMPLAR PROBLEMS3videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Assertion And Reason15videos
ELECTROMAGNETIC WAVES
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - NCERT Exemplar5videos
MAGNETISM AND MATTER
Similar Questions
Two capacitors, 3μF and 4μF, are individually charged across a 6V battery. After being disconnected from the battery, they are connected together with the negative place of one attached to the positive plate of the other. What is the common potential?
View SolutionTwo capacitors of capacitances 3μF and 6μF are charged to a potential of 12V each. They are now connected to each other, with the positive plate of each joined to the negative plate of the other. The potential difference across each will be
View SolutionThree capacitors of capacitances 2μF, 3μF and 6μF are connected in series with a 12 V battery. All the connecting wire are disconnected, the three positive plates are connected together and the three negative plates are connected together. Find the charges on the three capacitors after the reconnection.
View SolutionTwo capacitors of capacitances 3μF and 6μF are charged to a potential of 12V each. They are now connected to each other, with the positive plate of each joined to the negative plate of the other.
(A) the common potential will be 12V
(B) the loss in energy will be 576μJ
(c) the common potential will be 4V
(D) the loss in energy will be 144μJView SolutionTwo parallel plates capacitors A and B having capacitance of 1μFand5μF are charged separately to the same potential of 100 V. Now, the positive plate of A is connected to the negative plate of B and the negative plate of A to the positive plate of B. Find the final charges on each capacitors.
View SolutionA capacitor of capacitance 4μF is charged to 80V and another capacitor of capacitance 6μF is charged to 30V are connected to each other using zero resistance wires such that the positive plate of one capacitor is connected to the positive plate of the other. The energy lost by the 4μF capacitor in the process in X∗10−4J. Find the value of X.
View SolutionA capacitor of capacitance 4μF is charged to 80V and another capacitor of capacitance 6μF is charged to 30V are connected to each other using zero resistance wires such that the positive plate of one capacitor is connected to the positive plate of the other. The energy lost by the 4μF capacitor in the process in X∗10−4J. Find the value of X.
View SolutionTwo capacitor of capacitance 2μFand3μF respectively are charged to potential difference 20 V each. Now the capacitors are connected such that the positively chargd plate of one capacitory is connected to the negatively charged plate of the other. after the current in the circuit has become negligible, the potential difference across the 2μF capacitor is ____V.
View SolutionA capacitor A of capacitance 4μF is charged to 30V and another capacitor B of capacitance 2μF is charged to 15V. Now, the positive plate of A is connected to the negative plate of B and negative plate of A to the positive plate of B. find the final charge of each capacitor and loss of electrostatic energy in the process.
View SolutionA 10μF capacitor and a 20μF capacitor are connected in series across a 200V supply line. The chraged capacitors are then disconnected from the line and reconnected with their positive plates together and negative plates together and no external voltage is applied. what is the potential difference across each capacitor ?
View Solution