Question

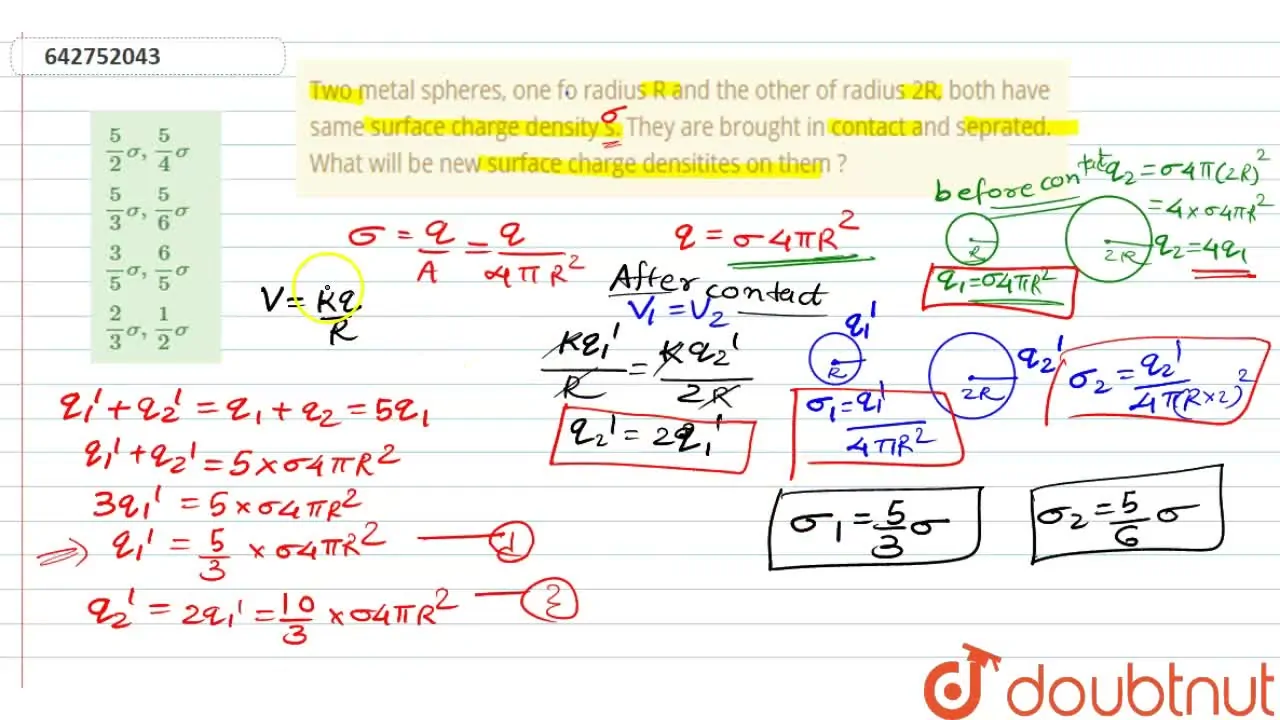
Two metal spheres, one fo radius R and the other of radius 2R, both have same surface charge density s. They are brought in contact and seprated. What will be new surface charge densitites on them ?

Options

A. `5/2sigma, 5/4sigma`
B. `5/3sigma, 5/6sigma`
C. `3/5sigma, 6/5sigma`
D. `2/3sigma,1/2sigma`

Answer

B

Explanation

To solve the problem of finding the new surface charge densities on two metal spheres after they are brought into contact and then separated, we can follow these steps:

Step 1: Understand the Initial Conditions
We have two metal spheres:
- Sphere 1: Radius = R, Surface Charge Density = σ
- Sphere 2: Radius = 2R, Surface Charge Density = σ

Step 2: Calculate Initial Charges
The charge on a sphere can be calculated using the formula:
\( Q = \sigma \times A \)
where \( A \) is the surface area of the sphere.

For Sphere 1 (radius R):
\( Q_1 = \sigma \times 4\pi R^2 \)

For Sphere 2 (radius 2R):
\( Q_2 = \sigma \times 4\pi (2R)^2 = \sigma \times 4\pi \times 4R^2 = 4\sigma \times 4\pi R^2 \)
Thus, we can say:
\( Q_2 = 4Q_1 \)

Step 3: Bringing the Spheres in Contact
When the two spheres are brought into contact, charge will redistribute between them until they reach the same electric potential. The potential \( V \) of a sphere is given by:
\( V = \frac{kQ}{R} \)
where \( k \) is Coulomb's constant.

After contact, let the new charges be \( Q_1' \) and \( Q_2' \). The potentials of both spheres must be equal:
\( \frac{kQ_1'}{R} = \frac{kQ_2'}{2R} \)
This simplifies to:
\( Q_2' = 2Q_1' \)

Step 4: Conservation of Charge
The total charge before contact must equal the total charge after contact:
\( Q_1 + Q_2 = Q_1' + Q_2' \)
Substituting the values we found:
\( Q_1 + 4Q_1 = Q_1' + 2Q_1' \)
This simplifies to:
\( 5Q_1 = 3Q_1' \)
Thus:
\( Q_1' = \frac{5}{3}Q_1 \)

Step 5: Calculate \( Q_2' \)
Using the relationship \( Q_2' = 2Q_1' \):
\( Q_2' = 2 \times \frac{5}{3}Q_1 = \frac{10}{3}Q_1 \)

Step 6: Calculate New Surface Charge Densities
Now we can find the new surface charge densities \( \sigma_1' \) and \( \sigma_2' \).

For Sphere 1:
\( \sigma_1' = \frac{Q_1'}{4\pi R^2} = \frac{\frac{5}{3}Q_1}{4\pi R^2} = \frac{\frac{5}{3}(\sigma \cdot 4\pi R^2)}{4\pi R^2} = \frac{5}{3}\sigma \)

For Sphere 2:
\( \sigma_2' = \frac{Q_2'}{4\pi (2R)^2} = \frac{\frac{10}{3}Q_1}{4\pi (4R^2)} = \frac{\frac{10}{3}(\sigma \cdot 4\pi R^2)}{16\pi R^2} = \frac{10}{3} \cdot \frac{1}{4} \sigma = \frac{5}{6}\sigma \)

Final Answer:
The new surface charge densities are:
- For Sphere 1: \( \sigma_1' = \frac{5}{3}\sigma \)
- For Sphere 2: \( \sigma_2' = \frac{5}{6}\sigma \)

---